Graphical model

In mathematics, the Heisenberg group, named after Werner Heisenberg, is the group of 3×3 upper triangular matrices of the form

${\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}$

or its generalizations under the operation of matrix multiplication. Elements a, b and c, can be taken from some (arbitrary) commutative ring with identity, often taken to be the ring of real numbers or the ring of integers.

The real Heisenberg group arises in the description of one-dimensional quantum mechanical systems. More generally, one can consider groups associated to n-dimensional systems, and most generally, to any symplectic vector space.

The three-dimensional case

In the three-dimensional case, the product of two Heisenberg matrices is given by:

${\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}{\begin{pmatrix}1&a'&c'\\0&1&b'\\0&0&1\\\end{pmatrix}}={\begin{pmatrix}1&a+a'&c+c'+ab'\\0&1&b+b'\\0&0&1\\\end{pmatrix}}\,.$

There are several prominent examples of the three-dimensional case.

Continuous Heisenberg group

If Buying, selling and renting HDB and personal residential properties in Singapore are simple and transparent transactions. Although you are not required to engage a real property salesperson (generally often known as a "public listed property developers In singapore agent") to complete these property transactions, chances are you'll think about partaking one if you are not accustomed to the processes concerned.

Professional agents are readily available once you need to discover an condominium for hire in singapore In some cases, landlords will take into account you more favourably in case your agent comes to them than for those who tried to method them by yourself. You need to be careful, nevertheless, as you resolve in your agent. Ensure that the agent you are contemplating working with is registered with the IEA – Institute of Estate Brokers. Whereas it might sound a hassle to you, will probably be worth it in the end. The IEA works by an ordinary algorithm and regulations, so you'll protect yourself in opposition to probably going with a rogue agent who prices you more than they should for his or her service in finding you an residence for lease in singapore.

There isn't any deal too small. Property agents who are keen to find time for any deal even if the commission is small are the ones you want on your aspect. Additionally they present humbleness and might relate with the typical Singaporean higher. Relentlessly pursuing any deal, calling prospects even without being prompted. Even if they get rejected a hundred times, they still come again for more. These are the property brokers who will find consumers what they need eventually, and who would be the most successful in what they do. 4. Honesty and Integrity

This feature is suitable for you who need to get the tax deductions out of your PIC scheme to your property agency firm. It's endorsed that you visit the correct site for filling this tax return software. This utility must be submitted at the very least yearly to report your whole tax and tax return that you're going to receive in the current accounting 12 months. There may be an official website for this tax filling procedure. Filling this tax return software shouldn't be a tough thing to do for all business homeowners in Singapore.

A wholly owned subsidiary of SLP Worldwide, SLP Realty houses 900 associates to service SLP's fast rising portfolio of residential tasks. Real estate is a human-centric trade. Apart from offering comprehensive coaching applications for our associates, SLP Realty puts equal emphasis on creating human capabilities and creating sturdy teamwork throughout all ranges of our organisational hierarchy. Worldwide Presence At SLP International, our staff of execs is pushed to make sure our shoppers meet their enterprise and investment targets. Under is an inventory of some notable shoppers from completely different industries and markets, who've entrusted their real estate must the expertise of SLP Worldwide.

If you're looking for a real estate or Singapore property agent online, you merely need to belief your instinct. It is because you don't know which agent is sweet and which agent will not be. Carry out research on a number of brokers by looking out the internet. As soon as if you find yourself certain that a selected agent is dependable and trustworthy, you'll be able to choose to utilize his partnerise find you a house in Singapore. More often than not, a property agent is considered to be good if she or he places the contact data on his web site. This is able to imply that the agent does not thoughts you calling them and asking them any questions regarding properties in Singapore. After chatting with them you too can see them of their office after taking an appointment.

Another method by way of which you could find out whether the agent is sweet is by checking the feedback, of the shoppers, on the website. There are various individuals would publish their comments on the web site of the Singapore property agent. You can take a look at these feedback and the see whether it will be clever to hire that specific Singapore property agent. You may even get in contact with the developer immediately. Many Singapore property brokers know the developers and you may confirm the goodwill of the agent by asking the developer., are real numbers (in the ring R) then one has the continuous Heisenberg group H₃(R).

It is a nilpotent Lie group.

In addition to the representation as real 3x3 matrices, the continuous Heisenberg group also has several different representations in terms of function spaces. By Stone–von Neumann theorem, there is a unique irreducible unitary representation of H in which its centre acts by a given nontrivial character. This representation has several important realizations, or models. In the Schrödinger model, the Heisenberg group acts on the space of square integrable functions. In the theta representation, it acts on the space of holomorphic functions on the upper half-plane; it is so named for its connection with the theta functions.

Discrete Heisenberg group

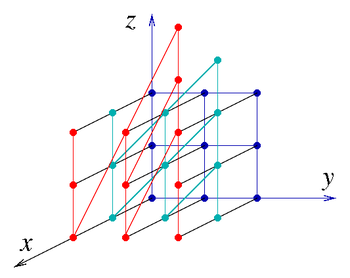
A portion of the Cayley graph of the discrete Heisenberg group, with generators x,y,z as in the text. (The coloring is only for visual aid.)

If Buying, selling and renting HDB and personal residential properties in Singapore are simple and transparent transactions. Although you are not required to engage a real property salesperson (generally often known as a "public listed property developers In singapore agent") to complete these property transactions, chances are you'll think about partaking one if you are not accustomed to the processes concerned.

Professional agents are readily available once you need to discover an condominium for hire in singapore In some cases, landlords will take into account you more favourably in case your agent comes to them than for those who tried to method them by yourself. You need to be careful, nevertheless, as you resolve in your agent. Ensure that the agent you are contemplating working with is registered with the IEA – Institute of Estate Brokers. Whereas it might sound a hassle to you, will probably be worth it in the end. The IEA works by an ordinary algorithm and regulations, so you'll protect yourself in opposition to probably going with a rogue agent who prices you more than they should for his or her service in finding you an residence for lease in singapore.

There isn't any deal too small. Property agents who are keen to find time for any deal even if the commission is small are the ones you want on your aspect. Additionally they present humbleness and might relate with the typical Singaporean higher. Relentlessly pursuing any deal, calling prospects even without being prompted. Even if they get rejected a hundred times, they still come again for more. These are the property brokers who will find consumers what they need eventually, and who would be the most successful in what they do. 4. Honesty and Integrity

This feature is suitable for you who need to get the tax deductions out of your PIC scheme to your property agency firm. It's endorsed that you visit the correct site for filling this tax return software. This utility must be submitted at the very least yearly to report your whole tax and tax return that you're going to receive in the current accounting 12 months. There may be an official website for this tax filling procedure. Filling this tax return software shouldn't be a tough thing to do for all business homeowners in Singapore.

A wholly owned subsidiary of SLP Worldwide, SLP Realty houses 900 associates to service SLP's fast rising portfolio of residential tasks. Real estate is a human-centric trade. Apart from offering comprehensive coaching applications for our associates, SLP Realty puts equal emphasis on creating human capabilities and creating sturdy teamwork throughout all ranges of our organisational hierarchy. Worldwide Presence At SLP International, our staff of execs is pushed to make sure our shoppers meet their enterprise and investment targets. Under is an inventory of some notable shoppers from completely different industries and markets, who've entrusted their real estate must the expertise of SLP Worldwide.

If you're looking for a real estate or Singapore property agent online, you merely need to belief your instinct. It is because you don't know which agent is sweet and which agent will not be. Carry out research on a number of brokers by looking out the internet. As soon as if you find yourself certain that a selected agent is dependable and trustworthy, you'll be able to choose to utilize his partnerise find you a house in Singapore. More often than not, a property agent is considered to be good if she or he places the contact data on his web site. This is able to imply that the agent does not thoughts you calling them and asking them any questions regarding properties in Singapore. After chatting with them you too can see them of their office after taking an appointment.

Another method by way of which you could find out whether the agent is sweet is by checking the feedback, of the shoppers, on the website. There are various individuals would publish their comments on the web site of the Singapore property agent. You can take a look at these feedback and the see whether it will be clever to hire that specific Singapore property agent. You may even get in contact with the developer immediately. Many Singapore property brokers know the developers and you may confirm the goodwill of the agent by asking the developer., are integers (in the ring Z) then one has the discrete Heisenberg group H₃(Z). It is a non-abelian nilpotent group. It has two generators,

$x={\begin{pmatrix}1&1&0\\0&1&0\\0&0&1\\\end{pmatrix}},\ \ y={\begin{pmatrix}1&0&0\\0&1&1\\0&0&1\\\end{pmatrix}}$

and relations

$z_{}^{}=xyx^{-1}y^{-1},\ xz=zx,\ yz=zy$,

where

$z={\begin{pmatrix}1&0&1\\0&1&0\\0&0&1\\\end{pmatrix}}$

is the generator of the center of H₃. (Note that the inverses of x, y, and z replace the 1 above the diagonal with −1.)

By Bass's theorem, it has a polynomial growth rate of order 4.

One can generate any element through

${\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}=y^{b}z^{c}x^{a}\,.$

Heisenberg group modulo an odd prime p

If one takes a, b, c in Z/p Z for an odd prime p, then one has the Heisenberg group modulo p. It is a group of order p³ with generators x,y and relations:

$z_{}^{}=xyx^{-1}y^{-1},\ x^{p}=y^{p}=z^{p}=1,\ xz=zx,\ yz=zy.$

Analogues of Heisenberg groups over finite fields of odd prime order p are called extra special groups, or more properly, extra special groups of exponent p. More generally, if the derived subgroup of a group G is contained in the center Z of G, then the map from G/Z × G/Z → Z is a skew-symmetric bilinear operator on abelian groups. However, requiring that G/Z be a finite vector space requires the Frattini subgroup of G to be contained in the center, and requiring that Z be a one dimensional vector space over Z/p Z requires that Z have order p, so if G is not abelian, then G is extra special. If G is extra special but does not have exponent p, then the general construction below applied to the symplectic vector space G/Z does not yield a group isomorphic to G.

Heisenberg group modulo 2

The Heisenberg group modulo 2 is of order 8 and is isomorphic to the dihedral group D₄ (the symmetries of a square). Observe that if

$x={\begin{pmatrix}1&1&0\\0&1&0\\0&0&1\\\end{pmatrix}},\ \ y={\begin{pmatrix}1&0&0\\0&1&1\\0&0&1\\\end{pmatrix}}$.

Then

$xy={\begin{pmatrix}1&1&1\\0&1&1\\0&0&1\\\end{pmatrix}},$

and

$yx={\begin{pmatrix}1&1&0\\0&1&1\\0&0&1\\\end{pmatrix}}.$

The elements x and y correspond to reflexions (with 45° between them), whereas xy and yx correspond to rotations by 90°. The other reflexions are xyx and yxy, and rotation by 180° is xyxy (=yxyx).

Higher dimensions

More general Heisenberg groups H_n may be defined for higher dimensions in Euclidean space, and more generally on symplectic vector spaces. The simplest general case is the real Heisenberg group of dimension 2n+1, for any integer n ≥ 1. As a group of matrices, H_n (or H_n(R) to indicate this is the Heisenberg group over the ring R or real numbers) is defined as the group of square matrices of size n+2 with entries in R:

${\begin{bmatrix}1&\mathbf {a} &c\\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}$

where

a is a row vector of length n,

b is a column vector of length n,

I_n is the identity matrix of size n.

Group Structure

This is indeed a group, as is shown by the multiplication:

${\begin{bmatrix}1&\mathbf {a} &c\\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}\cdot {\begin{bmatrix}1&\mathbf {a} '&c'\\0&I_{n}&\mathbf {b} '\\0&0&1\end{bmatrix}}={\begin{bmatrix}1&\mathbf {a} +\mathbf {a} '&c+c'+\mathbf {a} \cdot \mathbf {b} '\\0&I_{n}&\mathbf {b} +\mathbf {b} '\\0&0&1\end{bmatrix}}$

and

${\begin{bmatrix}1&\mathbf {a} &c\\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}\cdot {\begin{bmatrix}1&-\mathbf {a} &-c+\mathbf {a} \cdot \mathbf {b} \\0&I_{n}&-\mathbf {b} \\0&0&1\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&I_{n}&0\\0&0&1\end{bmatrix}}.$

The Heisenberg group is a connected, simply-connected Lie group whose Lie algebra consists of matrices

${\begin{bmatrix}0&\mathbf {a} &c\\0&0_{n}&\mathbf {b} \\0&0&0\end{bmatrix}},$

where

a is a row vector of length n,

b is a column vector of length n,

0_n is the zero matrix of size n.

Exponential Map

The exponential map is given by the following expression

$\exp {\begin{bmatrix}0&\mathbf {a} &c\\0&0_{n}&\mathbf {b} \\0&0&0\end{bmatrix}}=\sum _{k=0}^{\infty }{\frac {1}{k!}}{\begin{bmatrix}0&\mathbf {a} &c\\0&0_{n}&\mathbf {b} \\0&0&0\end{bmatrix}}^{k}={\begin{bmatrix}1&\mathbf {a} &c+{1 \over 2}\mathbf {a} \cdot \mathbf {b} \\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}.$

By letting e₁, ..., e_n be the canonical basis of Rⁿ, and setting

$p_{i}={\begin{bmatrix}0&\operatorname {e} _{i}^{\mathrm {T} }&0\\0&0_{n}&0\\0&0&0\end{bmatrix}},$

$q_{j}={\begin{bmatrix}0&0&0\\0&0_{n}&\operatorname {e} _{j}\\0&0&0\end{bmatrix}},$

$z={\begin{bmatrix}0&0&1\\0&0_{n}&0\\0&0&0\end{bmatrix}},$

the associated Lie algebra can be characterized by the canonical commutation relations,

${\begin{bmatrix}p_{i},q_{j}\end{bmatrix}}=\delta _{ij}z,\qquad \qquad {\begin{bmatrix}p_{i},z\end{bmatrix}}=0,\qquad {\begin{bmatrix}q_{j},z\end{bmatrix}}=0~,$

where p₁, ..., p_n, q₁, ..., q_n, z are the algebra generators.

In particular, z is a central element of the Heisenberg Lie algebra. Note that the Lie algebra of the Heisenberg group is nilpotent. The exponential map of a nilpotent Lie algebra is a diffeomorphism between the Lie algebra and the unique associated connected, simply-connected Lie group.

This discussion (aside from statements referring to dimension and Lie group) applies if we replace R by any commutative ring A. The corresponding group is denoted H_n(A ). Under the additional assumption that the prime 2 is invertible in the ring A, the exponential map is also defined, since it reduces to a finite sum and has the form above (i.e. A could be a ring Z/p Z with an odd prime p or any field of characteristic 0).

On symplectic vector spaces

The general abstraction of a Heisenberg group is constructed from any symplectic vector space. For example, let (V,ω) be a finite dimensional real symplectic vector space (so ω is a nondegenerate skew symmetric bilinear form on V). The Heisenberg group H(V) on (V,ω) (or simply V for brevity) is the set V×R endowed with the group law

$(v,t)\cdot (v',t')=\left(v+v',t+t'+{\tfrac {1}{2}}\omega (v,v')\right).$

The Heisenberg group is a central extension of the additive group V. Thus there is an exact sequence

$0\to \mathbf {R} \to H(V)\to V\to 0.$

Any symplectic vector space admits a Darboux basis {e_j,f^k}_{1 ≤ j,k ≤ n} satisfying ω(e_j,f^k) = δ_j^k and where 2n is the dimension of V (the dimension of V is necessarily even). In terms of this basis, every vector decomposes as

$v=q^{a}\mathbf {e} _{a}+p_{a}\mathbf {f} ^{a}.$

The q^a and p_a are canonically conjugate coordinates.

If {e_j, f^k}_{1 ≤ j,k ≤ n} is a Darboux basis for V, then let {E} be a basis for R, and {e_j, f^k, E}_{1 ≤ j,k ≤ n} is the corresponding basis for V×R. A vector in H(V) is then given by

$v=q^{a}\mathbf {e} _{a}+p_{a}\mathbf {f} ^{a}+tE$

and the group law becomes

$(p,q,t)\cdot (p',q',t')=\left(p+p',q+q',t+t'+{\frac {1}{2}}(pq'-p'q)\right).$

Because the underlying manifold of the Heisenberg group is a linear space, vectors in the Lie algebra can be canonically identified with vectors in the group. The Lie algebra of the Heisenberg group is given by the commutation relation

${\begin{bmatrix}(v_{1},t_{1}),(v_{2},t_{2})\end{bmatrix}}=\omega (v_{1},v_{2})$

or written in terms of the Darboux basis

$[\mathbf {e} _{a},\mathbf {f} ^{b}]=\delta _{a}^{b}$

and all other commutators vanish.

It is also possible to define the group law in a different way but which yields a group isomorphic to the group we have just defined. To avoid confusion, we will use u instead of t, so a vector is given by

$v=q^{a}\mathbf {e} _{a}+p_{a}\mathbf {f} ^{a}+uE$

and the group law is

$(p,q,u)\cdot (p',q',u')=(p+p',q+q',u+u'+pq').$

An element of the group

$v=q^{a}\mathbf {e} _{a}+p_{a}\mathbf {f} ^{a}+uE$

can then be expressed as a matrix

${\begin{bmatrix}1&p&u\\0&I_{n}&q\\0&0&1\end{bmatrix}}$ ,

which gives a faithful matrix representation of H(V). The u in this formulation is related to t in our previous formulation by $u=t+{\tfrac {1}{2}}pq$, so that the t value for the product comes to

$u+u'+pq'-{\tfrac {1}{2}}(p+p')(q+q')$

$=t+{\tfrac {1}{2}}pq+t'+{\tfrac {1}{2}}p'q'+pq'-{\tfrac {1}{2}}(p+p')(q+q')$

$=t+t'+{\tfrac {1}{2}}(pq'-p'q)$ ,

as before.

The isomorphism to the group using upper triangular matrices relies on the decomposition of V into a Darboux basis, which amounts to a choice of isomorphism V ≅ U ⊕ U*. Although the new group law yields a group isomorphic to the one given higher up, the group with this law is sometimes referred to as the polarized Heisenberg group as a reminder that this group law relies on a choice of basis (a choice of a Lagrangian subspace of V is a polarization).

To any Lie algebra, there is a unique connected, simply connected Lie group G. All other connected Lie groups with the same Lie algebra as G are of the form G/N where N is a central discrete group in G. In this case, the center of H(V) is R and the only discrete subgroups are isomorphic to Z. Thus H(V)/Z is another Lie group which shares this Lie algebra. Of note about this Lie group is that it admits no faithful finite dimensional representations; it is not isomorphic to any matrix group. It does however have a well-known family of infinite-dimensional unitary representations.

The connection with the Weyl algebra

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

The Lie algebra ${\mathfrak {h}}_{n}$ of the Heisenberg group was described above as a Lie algebra of matrices. The Poincaré–Birkhoff–Witt theorem applies to determine the universal enveloping algebra $U({\mathfrak {h}}_{n})$. Among other properties, the universal enveloping algebra is an associative algebra into which ${\mathfrak {h}}_{n}$ injectively imbeds. By Poincaré–Birkhoff–Witt, it is the free vector space generated by the monomials

$z^{j}p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{n}^{k_{n}}q_{1}^{\ell _{1}}q_{2}^{\ell _{2}}\cdots q_{n}^{\ell _{n}}$

where the exponents are all non-negative. Thus $U({\mathfrak {h}}_{n})$ consists of real polynomials

$\sum _{j,{\vec {k}},{\vec {\ell }}}c_{j{\vec {k}}{\vec {\ell }}}\,\,z^{j}p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{n}^{k_{n}}q_{1}^{\ell _{1}}q_{2}^{\ell _{2}}\cdots q_{n}^{\ell _{n}}$

with the commutation relations

$p_{k}p_{\ell }=p_{\ell }p_{k},\quad q_{k}q_{\ell }=q_{\ell }q_{k},\quad p_{k}q_{\ell }-q_{\ell }p_{k}=\delta _{k\ell }z,\quad zp_{k}-p_{k}z=0,\quad zq_{k}-q_{k}z=0.$

The algebra $U({\mathfrak {h}}_{n})$ is closely related to the algebra of differential operators on Rⁿ with polynomial coefficients, since any such operator has a unique representation in the form

$P=\sum _{{\vec {k}},{\vec {\ell }}}c_{{\vec {k}}{\vec {\ell }}}\,\,\partial _{x_{1}}^{k_{1}}\partial _{x_{2}}^{k_{2}}\cdots \partial _{x_{n}}^{k_{n}}x_{1}^{\ell _{1}}x_{2}^{\ell _{2}}\cdots x_{n}^{\ell _{n}}$

This algebra is called the Weyl algebra. It follows from abstract nonsense that the Weyl algebra W_n is a quotient of $U({\mathfrak {h}}_{n})$. However, this is also easy to see directly from the above representations; viz. by the mapping

$z^{j}p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{n}^{k_{n}}q_{1}^{\ell _{1}}q_{2}^{\ell _{2}}\cdots q_{n}^{\ell _{n}}\,\mapsto \,\partial _{x_{1}}^{k_{1}}\partial _{x_{2}}^{k_{2}}\cdots \partial _{x_{n}}^{k_{n}}x_{1}^{\ell _{1}}x_{2}^{\ell _{2}}\cdots x_{n}^{\ell _{n}}.$

Representation theory

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

The representation theory of the Heisenberg group is fairly simple – later generalized by Mackey theory – and was the motivation for its introduction in quantum physics, as discussed below.

The key result is the Stone–von Neumann theorem, which, informally stated, says that (with certain technical assumptions) every representation of the Heisenberg group H_2n+1 is equivalent to the position operators and momentum operators on Rⁿ. Alternatively, that they are all equivalent to the Weyl algebra (or CCR algebra) on a symplectic space of dimension 2n.

More formally, there is a unique (up to scale) non-trivial central strongly continuous unitary representation.

Further, as the Heisenberg group is a semidirect product, its representation theory can be studied in terms of ergodic theory, via ergodic actions of the group, as in the work of George Mackey.

Applications

Weyl's parameterization of quantum mechanics

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. The application that led Hermann Weyl to an explicit realization of the Heisenberg group was the question of why the Schrödinger picture and Heisenberg picture are physically equivalent. Abstractly, the reason is the Stone–von Neumann theorem: there is a unique unitary representation with given action of the central Lie algebra element z, up to a unitary equivalence: the nontrivial elements of the algebra are all equivalent to the usual position and momentum operators.

Thus, the Schrödinger picture and Heisenberg picture are equivalent – they are just different ways of realizing this essentially unique representation.

Theta representation

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. The same uniqueness result was used by David Mumford for discrete Heisenberg groups, in his theory of equations defining abelian varieties. This is a large generalization of the approach used in Jacobi's elliptic functions, which is the case of the modulo 2 Heisenberg group, of order 8. The simplest case is the theta representation of the Heisenberg group, of which the discrete case gives the theta function.

Fourier analysis

The Heisenberg group also occurs in Fourier analysis, where it is used in some formulations of the Stone–von Neumann theorem. In this case, the Heisenberg group can be understood to act on the space of square integrable functions; the result is a representation of the Heisenberg groups sometimes called the Weyl representation.

As a sub-Riemannian manifold

The three-dimensional Heisenberg group H₃(R) on the reals can also be understood to be a smooth manifold, and specifically, a simple example of a sub-Riemannian manifold. Given a point p=(x,y,z) in R³, define a differential 1-form Θ at this point as

$\Theta _{p}=dz-{\frac {1}{2}}\left(xdy-ydx\right).$

This one-form belongs to the cotangent bundle of R³; that is,

$\Theta _{p}:T_{p}\mathbf {R} ^{3}\to \mathbf {R}$

is a map on the tangent bundle. Let

$H_{p}=\{v\in T_{p}\mathbf {R} ^{3}\mid \Theta _{p}(v)=0\}.$

It can be seen that H is a subbundle of the tangent bundle TR³. A cometric on H is given by projecting vectors to the two-dimensional space spanned by vectors in the x and y direction. That is, given vectors $v=(v_{1},v_{2},v_{3})$ and $w=(w_{1},w_{2},w_{3})$ in TR³, the inner product is given by

$\langle v,w\rangle =v_{1}w_{1}+v_{2}w_{2}.$

The resulting structure turns H into the manifold of the Heisenberg group. An orthonormal frame on the manifold is given by the Lie vector fields

$X={\frac {\partial }{\partial x}}-{\frac {1}{2}}y{\frac {\partial }{\partial z}},$

$Y={\frac {\partial }{\partial y}}+{\frac {1}{2}}x{\frac {\partial }{\partial z}},$

$Z={\frac {\partial }{\partial z}},$

which obey the relations [X,Y]=Z and [X,Z]=[Y,Z]=0. Being Lie vector fields, these form a left-invariant basis for the group action. The geodesics on the manifold are spirals, projecting down to circles in two dimensions. That is, if

$\gamma (t)=(x(t),y(t),z(t))$

is a geodesic curve, then the curve $c(t)=(x(t),y(t))$ is an arc of a circle, and

$z(t)={\frac {1}{2}}\int _{c}xdy-ydx$

with the integral limited to the two-dimensional plane. That is, the height of the curve is proportional to the area of the circle subtended by the circular arc, which follows by Stokes' theorem.

See also

• Weyl quantization
• Stone–von Neumann theorem

References

• Ernst Binz & Sonja Pods (2008) Geometry of Heisenberg Groups American Mathematical Society,ISBN 978-0-8218-4495-3.
• 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
  
  My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
• Roger Evans Howe (1980) "On the role of the Heisenberg group in harmonic analysis", Bulletin of the American Mathematical Society 3(2):821.
• A.A. Kirilov (2004) Lectures on the Orbit Method, Chapter 2: "Representations and Orbits of the Heisenberg Group", American Mathematical Society, ISBN 0-8218-3530-0 .
• G Mackey (1976) The theory of Unitary Group Representations (Chicago Lectures in Mathematics) University Of Chicago Press (1976) ISBN 978-0226500522 .

External links

• Groupprops, The Group Properties Wiki Unitriangular matrix group UT(3,p)