Finite set: Difference between revisions
en>DexDor →References: rm Terminology cat (the title may be a term, but the article is not about language) |
en>JRSpriggs Undid revision 566676304 by 2002:65DE:7B18:0:0:0:65DE:7B18 (talk) wrong |
||
| Line 1: | Line 1: | ||
:''Not to be confused with [[Ferrimagnetism]]; for an overview see [[Magnetism]]'' | |||
[[Image:MagnetEZ.jpg|thumb|A magnet made of [[alnico]], an iron alloy. Ferromagnetism is the physical theory which explains how materials become magnets.]] | |||
'''Ferromagnetism''' is the basic mechanism by which certain materials (such as [[iron]]) form [[permanent magnet]]s, or are attracted to [[magnet]]s. In [[physics]], several different types of [[magnetism]] are distinguished. Ferromagnetism (including [[ferrimagnetism]])<ref>{{cite book|last=Chikazumi|first=Sōshin|title=Physics of ferromagnetism|year=2009|publisher=Oxford University Press|location=Oxford|isbn=9780199564811|edition=2nd |others= English edition prepared with the assistance of C.D. Graham, Jr |page=118}}</ref> is the strongest type; it is the only type that creates forces strong enough to be felt, and is responsible for the common phenomena of magnetism [[Magnet#Common uses of magnets|encountered in everyday life]]. Other substances respond weakly to magnetic fields with two other types of magnetism, [[paramagnetism]] and [[diamagnetism]], but the forces are so weak that they can only be detected by sensitive instruments in a laboratory. An everyday example of ferromagnetism is a [[refrigerator magnet]] used to hold notes on a refrigerator door. The attraction between a magnet and ferromagnetic material is "the quality of magnetism first apparent to the ancient world, and to us today".<ref name="bozorth">Bozorth, Richard M. ''Ferromagnetism'', first published 1951, reprinted 1993 by [[IEEE]] Press, New York as a "Classic Reissue." ISBN 0-7803-1032-2.</ref> | |||
Permanent magnets (materials that can be [[Magnetization|magnetized]] by an external [[magnetic field]] and remain magnetized after the external field is removed) are either ferromagnetic or ferrimagnetic, as are other materials that are noticeably attracted to them. Only a few substances are ferromagnetic. The common ones are [[iron]], [[nickel]], [[cobalt]] and most of their alloys, some compounds of [[Rare earth magnet|rare earth metals]], and a few naturally-occurring minerals such as [[lodestone]]. | |||
Ferromagnetism is very important in industry and modern technology, and is the basis for many electrical and electromechanical devices such as [[electromagnet]]s, [[electric motor]]s, [[Electric generator|generators]], [[transformer]]s, and [[magnetic storage]] such as [[tape recorder]]s, and [[hard disk]]s. | |||
==History and distinction from ferrimagnetism== | |||
Historically, the term ''ferromagnet'' was used for any material that could exhibit spontaneous magnetization: a net magnetic moment in the absence of an external magnetic field. This general definition is still in common use. More recently, however, different classes of spontaneous magnetization have been identified when there is more than one magnetic ion per [[primitive cell]] of the material, leading to a stricter definition of "ferromagnetism" that is often used to distinguish it from ferrimagnetism. In particular, | |||
* a material is "ferromagnetic" in this narrower sense only if ''all'' of its magnetic ions add a positive contribution to the net magnetization. | |||
* If some of the magnetic ions ''subtract'' from the net magnetization (if they are partially ''anti''-aligned), then the material is "ferrimagnetic".<ref>{{cite journal|last=Herrera|first=J. M.|coauthors=Bachschmidt, A, Villain, F, Bleuzen, A, Marvaud, V, Wernsdorfer, W, Verdaguer, M|title=Mixed valency and magnetism in cyanometallates and Prussian blue analogues|journal=Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences|date=13 January 2008|volume=366|issue=1862|pages=127–138|doi=10.1098/rsta.2007.2145}}</ref> | |||
* If the moments of the aligned and anti-aligned ions balance completely so as to have zero net magnetization, despite the magnetic [[Order (crystal lattice)|ordering]], then it is an [[antiferromagnet]]. These alignment effects only occur at [[temperature]]s below a certain critical temperature, called the [[Curie temperature]] (for ferromagnets and ferrimagnets) or the [[Néel temperature]] (for antiferromagnets). | |||
Among the first investigations of ferromagnetism are the pioneering works of [[Aleksandr Stoletov]] on measurement of the [[magnetic permeability]] of ferromagnetics, known as the [[Stoletov curve]]. | |||
==Ferromagnetic materials==<!-- [[Ferromagnetic materials]] redirects here --> | |||
{{See also|Category:Ferromagnetic materials}} | |||
{| class="wikitable" style="float:right;margin:0 0 1em 1em;" | |||
|+ style="font-size: 80%"|Curie temperatures for some crystalline ferromagnetic (* = ferrimagnetic) materials<ref>{{cite book|last=Kittel|first=Charles|author-link=Charles Kittel|title=Introduction to Solid State Physics|edition=sixth|publisher=[[John Wiley and Sons]]|year=1986|isbn=0-471-87474-4}}</ref> | |||
|- | |||
! Material | |||
! Curie <br/>temp. (K) | |||
|- | |||
| [[Cobalt|Co]] | |||
| 1388 | |||
|- | |||
| [[Iron|Fe]] | |||
| 1043 | |||
|- | |||
| [[Iron(III) oxide|Fe<sub>2</sub>O<sub>3</sub>]]<sup>*</sup> | |||
| 948 | |||
|- | |||
| [[Iron(II,III) oxide|FeOFe<sub>2</sub>O<sub>3</sub>]]<sup>*</sup> | |||
| 858 | |||
|- | |||
| NiOFe<sub>2</sub>O<sub>3</sub><sup>*</sup> | |||
| 858 | |||
|- | |||
| [[Copper|Cu]]OFe<sub>2</sub>O<sub>3</sub><sup>*</sup> | |||
| 728 | |||
|- | |||
| MgOFe<sub>2</sub>O<sub>3</sub><sup>*</sup> | |||
| 713 | |||
|- | |||
| [[Manganese|Mn]][[Bismuth|Bi]] | |||
| 630 | |||
|- | |||
| [[Nickel|Ni]] | |||
| 627 | |||
|- | |||
| Mn[[Antimony|Sb]] | |||
| 587 | |||
|- | |||
| MnOFe<sub>2</sub>O<sub>3</sub><sup>*</sup> | |||
| 573 | |||
|- | |||
| [[Yttrium iron garnet|Y<sub>3</sub>Fe<sub>5</sub>O<sub>12</sub>]]<sup>*</sup> | |||
| 560 | |||
|- | |||
| [[Chromium(IV) oxide|CrO<sub>2</sub>]] | |||
| 386 | |||
|- | |||
| Mn[[Arsenic|As]] | |||
| 318 | |||
|- | |||
| [[Gadolinium|Gd]] | |||
| 292 | |||
|- | |||
| [[Dysprosium|Dy]] | |||
| 88 | |||
|- | |||
| [[Europium|Eu]]O | |||
| 69 | |||
|- | |||
<!-- The numbers in this table currently come from Kittel, as referenced in the text. Please do not add new numbers without adding the corresponding reference. --> | |||
|} | |||
The table on the right lists a selection of ferromagnetic and ferrimagnetic compounds, along with the temperature above which they cease to exhibit spontaneous magnetization (see [[Ferromagnetism#Curie temperature|Curie temperature]]). | |||
Ferromagnetism is a property not just of the chemical make-up of a material, but of its crystalline structure and microscopic organization. There are ferromagnetic metal alloys whose constituents are not themselves ferromagnetic, called [[Heusler alloy]]s, named after [[Fritz Heusler]]. Conversely there are non-magnetic alloys, such as types of [[stainless steel]], composed almost exclusively of ferromagnetic metals. | |||
One can also make amorphous (non-crystalline) ferromagnetic metallic alloys by very rapid [[quenching]] (cooling) of a liquid alloy. These have the advantage that their properties are nearly isotropic (not aligned along a crystal axis); this results in low [[coercivity]], low [[hysteresis]] loss, high permeability, and high electrical resistivity. One such typical material is a transition metal-metalloid alloy, made from about 80% transition metal (usually Fe, Co, or Ni) and a metalloid component ([[Boron|B]], [[Carbon|C]], [[Silicon|Si]], [[Phosphorus|P]], or [[Aluminium|Al]]) that lowers the melting point. | |||
<!--changes here are not correct; commenting out until sorted out on talk: One example of such an amorphous alloy is Fe<sub>80</sub>B<sub>20</sub> (Metglas 2605) which has a Curie temperature of 647 K and a room-temperature (300 K) saturation magnetization of 1.58 [[tesla (unit)|teslas]] (1,257 [[gauss]]), compared with 1,043 K and 2.15 T (1,707 gauss) for pure iron from above. The melting point, or more precisely the glass transition temperature, is only 714 K for the alloy versus a melting point of 1,811 K for pure iron.--> | |||
A relatively new class of exceptionally strong ferromagnetic materials are the [[rare-earth magnet]]s. They contain lanthanide elements that are known for their ability to carry large magnetic moments in well-localized f-orbitals. | |||
===Actinide ferromagnets=== | |||
A number of [[actinide]] compounds are ferromagnets at room temperature or become ferromagnets below the [[Curie temperature]] (T<sub>C</sub>). [[Plutonium|Pu]][[Phosphorus|P]] is one actinide [[Nitrogen family|pnictide]] that is a paramagnet and has [[Cubic crystal system|cubic symmetry]] at [[room temperature]], but upon cooling undergoes a lattice distortion to [[Tetragonal crystal system|tetragonal]] when cooled to below its T<sub>c</sub> = 125 K. PuP has an [[easy axis]] of <100>,<ref name=Lander>{{cite journal |author=Lander GH, Lam DJ |title=Neutron diffraction study of PuP: The electronic ground state |journal=Phys. Rev. B|year=1976 |volume=14 |issue=9 |pages=4064–7 |doi=10.1103/PhysRevB.14.4064|bibcode = 1976PhRvB..14.4064L }}</ref> so that | |||
:<math>\frac{c}{a} - 1 = -(31 \pm 1) \times 10^{-4}</math> | |||
at 5 K.<ref name=Mueller>{{cite journal |author=Mueller MH, Lander GH, Hoff HA, Knott HW, Reddy JF |title=Lattice distortions measured in actinide ferromagnets PuP, NpFe<sub>2</sub>, and NpNi<sub>2</sub> |journal= J Phys Colloque C4, supplement |date=Apr 1979 |volume=40 |issue=4 |pages=C4–68–C4–69 |url=http://hal.archives-ouvertes.fr/docs/00/21/88/17/PDF/ajp-jphyscol197940C421.pdf}}</ref> The lattice distortion is presumably a consequence of strain induced by the magnetoelastic interactions as the [[magnetic moment]]s aligned parallel within [[magnetic domain]]s. | |||
In [[Neptunium|Np]]Fe<sub>2</sub> the easy axis is <111>.<ref name=Aldred>{{cite journal |author=Aldred AT, Dunlap BD, Lam DJ, Lander GH, Mueller MH, Nowik I |title=Magnetic properties of neptunium Laves phases: NpMn<sub>2</sub>, NpFe<sub>2</sub>, NpCo<sub>2</sub>, and NpNi<sub>2</sub> |journal=Phys. Rev. B|year=1975 |volume=11 |issue=1 |pages=530–44 |doi=10.1103/PhysRevB.11.530|bibcode = 1975PhRvB..11..530A }}</ref> Above T<sub>C</sub> ~500 K NpFe<sub>2</sub> is also paramagnetic and cubic. Cooling below the Curie temperature produces a rhombohedral distortion wherein the rhombohedral angle changes from 60° (cubic phase) to 60.53°. An alternate description of this distortion is to consider the length c along the unique trigonal axis (after the distortion has begun) and a as the distance in the plane perpendicular to c. In the cubic phase this reduces to <math>\scriptstyle\frac{c}{a}</math> = 1.00. Below the [[Curie temperature]] | |||
:<math>\frac{c}{a} - 1 = -(120 \pm 5) \times 10^{-4}</math> | |||
which is the largest strain in any [[actinide]] compound.<ref name=Mueller/> NpNi<sub>2</sub> undergoes a similar lattice distortion below T<sub>C</sub> = 32 K, with a strain of (43 ± 5) × 10<sup>−4</sup>.<ref name=Mueller/> NpCo<sub>2</sub> is a ferrimagnet below 15 K. | |||
===Lithium gas=== | |||
In 2009, a team of [[MIT]] physicists demonstrated that a lithium gas cooled to less than one kelvin can exhibit ferromagnetism.<ref>{{cite journal |author=G-B Jo, Y-R Lee, J-H Choi, C. A. Christensen, T. H. Kim, J. H. Thywissen, D. E. Pritchard, and W. Ketterle |title=Itinerant Ferromagnetism in a Fermi Gas of Ultracold Atoms |journal= Science |year=2009 |volume=325 |pages=1521–1524 |doi=10.1126/science.1177112 |pmid=19762638 |issue=5947 |bibcode = 2009Sci...325.1521J }}</ref> The team cooled [[fermion]]ic lithium-6 to less than 150 billionths of one kelvin above absolute zero using infrared [[laser cooling]]. This demonstration is the first time that ferromagnetism has been demonstrated in a gas. | |||
==Explanation== | |||
The [[Bohr–van Leeuwen theorem]] shows that magnetism cannot occur in purely classical solids. Without [[quantum mechanics]], there would be no [[diamagnetism]], paramagnetism or ferromagnetism. The property of ferromagnetism is due to the direct influence of two effects from quantum mechanics: [[spin (physics)|spin]] and the [[Pauli exclusion principle]].<ref>{{cite book | |||
|last = Feynman | |||
|first = Richard P. | |||
|coauthors = Robert Leighton, Matthew Sands | |||
|title = The Feynman Lectures on Physics, Vol.2 | |||
|publisher = Addison-Wesley | |||
|year = 1963 | |||
|location = USA | |||
|pages = Ch. 37}}</ref> | |||
===Origin of magnetism=== | |||
One of the fundamental properties of an [[electron]] (besides that it carries charge) is that it has a [[Electron magnetic dipole moment|magnetic dipole moment]], i.e., it behaves itself as a tiny magnet. This dipole moment comes from the more fundamental property of the electron that it has quantum mechanical [[Spin (physics)|spin]]. The quantum mechanical nature of this spin causes the electron to only be able to be in two states, with the magnetic field either pointing "up" or "down" (for any choice of up and down). The spin of the electrons in atoms is the main source of ferromagnetism, although there is also a contribution from the [[planetary orbit|orbital]] [[angular momentum]] of the electron about the [[nucleus (atomic structure)|nucleus]]. When these tiny magnetic dipoles are aligned in the same direction, their individual magnetic fields add together to create a measurable macroscopic field. | |||
However, in materials with a filled [[electron shell]], the total dipole moment of the electrons is zero because the spins are in up/down pairs. Only atoms with partially filled shells (i.e., unpaired spins) can have a net magnetic moment, so ferromagnetism only occurs in materials with partially filled shells. Because of [[Hund's rules]], the first few electrons in a shell tend to have the same spin, thereby increasing the total dipole moment. | |||
These unpaired dipoles (often called simply "spins" even though they also generally include angular momentum) tend to align in parallel to an external magnetic field, an effect called paramagnetism. Ferromagnetism involves an additional phenomenon, however: The dipoles tend to align spontaneously, giving rise to a [[spontaneous magnetization]], even when there is no applied field. | |||
===Exchange interaction=== | |||
{{Main|Exchange interaction}} | |||
According to classical [[electromagnetism]], two nearby magnetic dipoles will tend to align in ''opposite'' directions, so their magnetic fields will oppose one another and cancel out. However, this effect is very weak, because the magnetic fields generated by individual spins are small and the resulting alignment is easily destroyed by [[thermal fluctuations]]. In a few materials, a much stronger interaction between spins arises because the change in the direction of the spin leads to a change in [[electrostatic]] repulsion between neighboring electrons, due to a particular [[Quantum mechanics|quantum mechanical]] effect called the [[exchange interaction]]. At short distances, the exchange interaction is much stronger than the dipole-dipole magnetic interaction. As a result, in a few materials, the ferromagnetic ones, nearby spins tend to align in the same direction. | |||
The exchange interaction is related to the [[Pauli exclusion principle]], which says that two electrons with the same spin cannot also have the same "position". Therefore, under certain conditions, when the [[atomic orbital|orbitals]] of the unpaired outer [[valence electron]]s from adjacent atoms overlap, the distributions of their electric charge in space are further apart when the electrons have parallel spins than when they have opposite spins. This reduces the [[electrostatic energy]] of the electrons when their spins are parallel compared to their energy when the spins are anti-parallel, so the parallel-spin state is more stable. In simple terms, the electrons, which repel one another, can move "further apart" by aligning their spins, so the spins of these electrons tend to line up. This difference in energy is called the [[exchange energy]]. | |||
The materials in which the exchange interaction is much stronger than the competing dipole-dipole interaction are frequently called ''magnetic materials''. For instance, in iron (Fe) the exchange force is about 1000 times stronger than the dipole interaction. Therefore below the Curie temperature virtually all of the dipoles in a ferromagnetic material will be aligned. | |||
The [[exchange interaction]] is also responsible for the other types of spontaneous ordering of atomic magnetic moments occurring in magnetic solids, [[antiferromagnetism]] and ferrimagnetism. | |||
There are different exchange interaction mechanisms which create the magnetism in different ferromagnetic, ferrimagnetic, and antiferromagnetic substances. These mechanisms include [[Exchange_interaction#Direct_exchange_interactions_in_solids|direct exchange]], [[RKKY interaction|RKKY exchange]], [[double exchange]], and [[superexchange]]. | |||
===Magnetic anisotropy=== | |||
{{Main|Magnetic anisotropy}} | |||
Although the exchange interaction keeps spins aligned, it does not align them in a particular direction. Without [[magnetic anisotropy]], the spins in a magnet randomly change direction in response to [[thermal fluctuations]] and the magnet is [[superparamagnetic]]. There are several kinds of magnetic anisotropy, the most common of which is [[magnetocrystalline anisotropy]]. This is a dependence of the energy on the direction of magnetization relative to the [[crystallographic lattice]]. Another common source of anisotropy, [[inverse magnetostriction]], is induced by internal [[deformation (mechanics)|strains]]. [[Single-domain (magnetic)|Single-domain magnets]] also can have a ''shape anisotropy'' due to the magnetostatic effects of the particle shape. As the temperature of a magnet increases, the anisotropy tends to decrease, and there is often a [[superparamagnetism#Blocking temperature|blocking temperature]] at which a transition to superparamagnetism occurs.<ref name=Aharoni>{{cite book|last = Aharoni|first = Amikam|author-link=Amikam Aharoni|title=Introduction to the Theory of Ferromagnetism|publisher=[[Clarendon Press]]|year = 1996|isbn=0-19-851791-2|url=http://www.oup.com/us/catalog/general/subject/Physics/ElectricityMagnetism/?view=usa&ci=9780198508090}}</ref> | |||
===Magnetic domains=== | |||
[[File:Electromagnetic dynamic magnetic domain motion of grain oriented electrical silicon steel.gif|thumb|Electromagnetic dynamic magnetic domain motion of grain oriented electrical silicon steel]] | |||
[[File:Non Oriented Electrical Silicon Steel.png|thumb|Domain orientations in non-grain-oriented steel imaged with magneto-optical sensor and polarizer microscope.]] | |||
[[File:Magnetic domains of non oriented silicon or electrical steel.png|thumb|Magnetic domains of non-oriented silicon or electrical steel (recorded with CMOS-MagView).]] | |||
[[Image:Weiss-Bezirke1.png|thumb|Kerr micrograph of metal surface showing magnetic domains. The domains are the red and green stripes within each microcrystalline grain. The magnetic field in the red domains is in the opposite direction from the green domains.]] | |||
{{Main|Magnetic domain}} | |||
The above would seem to suggest that every piece of ferromagnetic material should have a strong magnetic field, since all the spins are aligned, yet iron and other ferromagnets are often found in an "unmagnetized" state. The reason for this is that a bulk piece of ferromagnetic material is divided into tiny ''[[magnetic domains]]''<ref name="Feynman">{{cite book | |||
| last = Feynman | |||
| first = Richard P. | |||
| coauthors = Robert B. Leighton, Matthew Sands | |||
| title = The Feynman Lectures on Physics, Vol. I | |||
| publisher = California Inst. of Technology | |||
| year = 1963 | |||
| location = USA | |||
| pages = 37.5–37.6 | |||
| url = http://books.google.com/books?id=bDF-uoUmttUC&pg=SA4-PA4}}</ref> (also known as ''Weiss domains''). Within each domain, the spins are aligned, but (if the bulk material is in its lowest energy configuration, i.e. ''unmagnetized''), the spins of separate domains point in different directions and their magnetic fields cancel out, so the object has no net large scale magnetic field. | |||
Ferromagnetic materials spontaneously divide into magnetic domains because the ''[[exchange interaction]]'' is a short-range force, so over long distances of many atoms the tendency of the magnetic dipoles to reduce their energy by orienting in opposite directions wins out. If all the dipoles in a piece of ferromagnetic material are aligned parallel, it creates a large magnetic field extending into the space around it. This contains a lot of [[magnetostatics|magnetostatic]] energy. The material can reduce this energy by splitting into many domains pointing in different directions, so the magnetic field is confined to small local fields in the material, reducing the volume of the field. The domains are separated by thin [[Domain wall (magnetism)|domain wall]]s a number of molecules thick, in which the direction of magnetization of the dipoles rotates smoothly from one domain's direction to the other. | |||
===Magnetized materials=== | |||
Thus, a piece of iron in its lowest energy state ("unmagnetized") generally has little or no net magnetic field. However, if it is placed in a strong enough external magnetic field, the domain walls will move, reorienting the domains so more of the dipoles are aligned with the external field. The domains will remain aligned when the external field is removed, creating a magnetic field of their own extending into the space around the material, thus creating a "permanent" magnet. The domains do not go back to their original minimum energy configuration when the field is removed because the domain walls tend to become 'pinned' or 'snagged' on defects in the crystal lattice, preserving their parallel orientation. This is shown by the [[Barkhausen effect]]: as the magnetizing field is changed, the magnetization changes in thousands of tiny discontinuous jumps as the domain walls suddenly "snap" past defects. | |||
This magnetization as a function of the external field is described by a [[Hysteresis loop|hysteresis curve]]. Although this state of aligned domains found in a piece of magnetized ferromagnetic material is not a minimal-energy configuration, it is [[metastable]], and can persist for long periods, as shown by samples of [[magnetite]] from the sea floor which have maintained their magnetization for millions of years. | |||
Alloys used for the strongest permanent magnets are "hard" alloys made with many defects in their crystal structure where the domain walls "catch" and stabilize. The net magnetization can be destroyed by heating and then cooling ([[Annealing (metallurgy)|annealing]]) the material without an external field, however. The thermal motion allows the domain boundaries to move, releasing them from any defects, to return to their low-energy unaligned state. | |||
===Curie temperature=== | |||
{{Main|Curie temperature}} | |||
As the temperature increases, thermal motion, or [[entropy]], competes with the ferromagnetic tendency for dipoles to align. When the temperature rises beyond a certain point, called the '''Curie temperature''', there is a second-order [[phase transition]] and the system can no longer maintain a spontaneous magnetization, although it still responds paramagnetically to an external field. Below that temperature, there is a [[spontaneous symmetry breaking]] and magnetic moments become aligned with their neighbors. The Curie temperature itself is a [[critical point (thermodynamics)|critical point]], where the [[magnetic susceptibility]] is theoretically infinite and, although there is no net magnetization, domain-like spin correlations fluctuate at all length scales. | |||
The study of ferromagnetic phase transitions, especially via the simplified [[Ising model|Ising]] spin model, had an important impact on the development of statistical physics. There, it was first clearly shown that [[mean field theory]] approaches failed to predict the correct behavior at the critical point (which was found to fall under a ''universality class'' that includes many other systems, such as liquid-gas transitions), and had to be replaced by [[renormalization group]] theory.{{citation needed|date=December 2012}} | |||
==See also== | |||
*[[Ferromagnetic material properties]] | |||
*[[Thermo-magnetic motor]] | |||
*[[Orbital magnetization]] | |||
==References== | |||
{{Reflist}} | |||
==External links== | |||
*[http://www.lightandmatter.com/html_books/0sn/ch11/ch11.html Electromagnetism] – a chapter from an online textbook | |||
*{{cite web | |||
|last = Sandeman | |||
|first = Karl | |||
|title = Ferromagnetic Materials | |||
|work = DoITPoMS | |||
|publisher = Dept. of Materials Sci. and Metallurgy, Univ. of Cambridge | |||
|date = January 2008 | |||
|url = http://www.msm.cam.ac.uk/doitpoms/tlplib/ferromagnetic/printall.php | |||
|accessdate = 2008-08-27}} Detailed nonmathematical description of ferromagnetic materials with animated illustrations | |||
* [http://www.cond-mat.de/events/correl13/manuscripts/pavarini.pdf Magnetism: Models and Mechanisms] in E. Pavarini, E. Koch, and U. Schollwöck: Emergent Phenomena in Correlated Matter, Jülich 2013, ISBN 978-3-89336-884-6 | |||
{{magnetic states}} | |||
[[Category:Quantum phases]] | |||
[[Category:Concepts in physics]] | |||
[[Category:Magnetic alloys]] | |||
[[Category:Magnetic ordering]] | |||
[[Category:Phase transitions]] | |||
Revision as of 08:19, 1 August 2013
- Not to be confused with Ferrimagnetism; for an overview see Magnetism

Ferromagnetism is the basic mechanism by which certain materials (such as iron) form permanent magnets, or are attracted to magnets. In physics, several different types of magnetism are distinguished. Ferromagnetism (including ferrimagnetism)[1] is the strongest type; it is the only type that creates forces strong enough to be felt, and is responsible for the common phenomena of magnetism encountered in everyday life. Other substances respond weakly to magnetic fields with two other types of magnetism, paramagnetism and diamagnetism, but the forces are so weak that they can only be detected by sensitive instruments in a laboratory. An everyday example of ferromagnetism is a refrigerator magnet used to hold notes on a refrigerator door. The attraction between a magnet and ferromagnetic material is "the quality of magnetism first apparent to the ancient world, and to us today".[2]
Permanent magnets (materials that can be magnetized by an external magnetic field and remain magnetized after the external field is removed) are either ferromagnetic or ferrimagnetic, as are other materials that are noticeably attracted to them. Only a few substances are ferromagnetic. The common ones are iron, nickel, cobalt and most of their alloys, some compounds of rare earth metals, and a few naturally-occurring minerals such as lodestone.
Ferromagnetism is very important in industry and modern technology, and is the basis for many electrical and electromechanical devices such as electromagnets, electric motors, generators, transformers, and magnetic storage such as tape recorders, and hard disks.
History and distinction from ferrimagnetism
Historically, the term ferromagnet was used for any material that could exhibit spontaneous magnetization: a net magnetic moment in the absence of an external magnetic field. This general definition is still in common use. More recently, however, different classes of spontaneous magnetization have been identified when there is more than one magnetic ion per primitive cell of the material, leading to a stricter definition of "ferromagnetism" that is often used to distinguish it from ferrimagnetism. In particular,
- a material is "ferromagnetic" in this narrower sense only if all of its magnetic ions add a positive contribution to the net magnetization.
- If some of the magnetic ions subtract from the net magnetization (if they are partially anti-aligned), then the material is "ferrimagnetic".[3]
- If the moments of the aligned and anti-aligned ions balance completely so as to have zero net magnetization, despite the magnetic ordering, then it is an antiferromagnet. These alignment effects only occur at temperatures below a certain critical temperature, called the Curie temperature (for ferromagnets and ferrimagnets) or the Néel temperature (for antiferromagnets).
Among the first investigations of ferromagnetism are the pioneering works of Aleksandr Stoletov on measurement of the magnetic permeability of ferromagnetics, known as the Stoletov curve.
Ferromagnetic materials
DTZ's public sale group in Singapore auctions all forms of residential, workplace and retail properties, outlets, homes, lodges, boarding homes, industrial buildings and development websites. Auctions are at present held as soon as a month.
We will not only get you a property at a rock-backside price but also in an space that you've got longed for. You simply must chill out back after giving us the accountability. We will assure you 100% satisfaction. Since we now have been working in the Singapore actual property market for a very long time, we know the place you may get the best property at the right price. You will also be extremely benefited by choosing us, as we may even let you know about the precise time to invest in the Singapore actual property market.
The Hexacube is offering new ec launch singapore business property for sale Singapore investors want to contemplate. Residents of the realm will likely appreciate that they'll customize the business area that they wish to purchase as properly. This venture represents one of the crucial expansive buildings offered in Singapore up to now. Many investors will possible want to try how they will customise the property that they do determine to buy by means of here. This location has offered folks the prospect that they should understand extra about how this course of can work as well.
Singapore has been beckoning to traders ever since the value of properties in Singapore started sky rocketing just a few years again. Many businesses have their places of work in Singapore and prefer to own their own workplace area within the country once they decide to have a everlasting office. Rentals in Singapore in the corporate sector can make sense for some time until a business has discovered a agency footing. Finding Commercial Property Singapore takes a variety of time and effort but might be very rewarding in the long term.
is changing into a rising pattern among Singaporeans as the standard of living is increasing over time and more Singaporeans have abundance of capital to invest on properties. Investing in the personal properties in Singapore I would like to applaud you for arising with such a book which covers the secrets and techniques and tips of among the profitable Singapore property buyers. I believe many novice investors will profit quite a bit from studying and making use of some of the tips shared by the gurus." – Woo Chee Hoe Special bonus for consumers of Secrets of Singapore Property Gurus Actually, I can't consider one other resource on the market that teaches you all the points above about Singapore property at such a low value. Can you? Condominium For Sale (D09) – Yong An Park For Lease
In 12 months 2013, c ommercial retails, shoebox residences and mass market properties continued to be the celebrities of the property market. Models are snapped up in report time and at document breaking prices. Builders are having fun with overwhelming demand and patrons need more. We feel that these segments of the property market are booming is a repercussion of the property cooling measures no.6 and no. 7. With additional buyer's stamp responsibility imposed on residential properties, buyers change their focus to commercial and industrial properties. I imagine every property purchasers need their property funding to understand in value.
| Material | Curie temp. (K) |
|---|---|
| Co | 1388 |
| Fe | 1043 |
| Fe2O3* | 948 |
| FeOFe2O3* | 858 |
| NiOFe2O3* | 858 |
| CuOFe2O3* | 728 |
| MgOFe2O3* | 713 |
| MnBi | 630 |
| Ni | 627 |
| MnSb | 587 |
| MnOFe2O3* | 573 |
| Y3Fe5O12* | 560 |
| CrO2 | 386 |
| MnAs | 318 |
| Gd | 292 |
| Dy | 88 |
| EuO | 69 |
The table on the right lists a selection of ferromagnetic and ferrimagnetic compounds, along with the temperature above which they cease to exhibit spontaneous magnetization (see Curie temperature).
Ferromagnetism is a property not just of the chemical make-up of a material, but of its crystalline structure and microscopic organization. There are ferromagnetic metal alloys whose constituents are not themselves ferromagnetic, called Heusler alloys, named after Fritz Heusler. Conversely there are non-magnetic alloys, such as types of stainless steel, composed almost exclusively of ferromagnetic metals.
One can also make amorphous (non-crystalline) ferromagnetic metallic alloys by very rapid quenching (cooling) of a liquid alloy. These have the advantage that their properties are nearly isotropic (not aligned along a crystal axis); this results in low coercivity, low hysteresis loss, high permeability, and high electrical resistivity. One such typical material is a transition metal-metalloid alloy, made from about 80% transition metal (usually Fe, Co, or Ni) and a metalloid component (B, C, Si, P, or Al) that lowers the melting point.
A relatively new class of exceptionally strong ferromagnetic materials are the rare-earth magnets. They contain lanthanide elements that are known for their ability to carry large magnetic moments in well-localized f-orbitals.
Actinide ferromagnets
A number of actinide compounds are ferromagnets at room temperature or become ferromagnets below the Curie temperature (TC). PuP is one actinide pnictide that is a paramagnet and has cubic symmetry at room temperature, but upon cooling undergoes a lattice distortion to tetragonal when cooled to below its Tc = 125 K. PuP has an easy axis of <100>,[5] so that
at 5 K.[6] The lattice distortion is presumably a consequence of strain induced by the magnetoelastic interactions as the magnetic moments aligned parallel within magnetic domains.
In NpFe2 the easy axis is <111>.[7] Above TC ~500 K NpFe2 is also paramagnetic and cubic. Cooling below the Curie temperature produces a rhombohedral distortion wherein the rhombohedral angle changes from 60° (cubic phase) to 60.53°. An alternate description of this distortion is to consider the length c along the unique trigonal axis (after the distortion has begun) and a as the distance in the plane perpendicular to c. In the cubic phase this reduces to = 1.00. Below the Curie temperature
which is the largest strain in any actinide compound.[6] NpNi2 undergoes a similar lattice distortion below TC = 32 K, with a strain of (43 ± 5) × 10−4.[6] NpCo2 is a ferrimagnet below 15 K.
Lithium gas
In 2009, a team of MIT physicists demonstrated that a lithium gas cooled to less than one kelvin can exhibit ferromagnetism.[8] The team cooled fermionic lithium-6 to less than 150 billionths of one kelvin above absolute zero using infrared laser cooling. This demonstration is the first time that ferromagnetism has been demonstrated in a gas.
Explanation
The Bohr–van Leeuwen theorem shows that magnetism cannot occur in purely classical solids. Without quantum mechanics, there would be no diamagnetism, paramagnetism or ferromagnetism. The property of ferromagnetism is due to the direct influence of two effects from quantum mechanics: spin and the Pauli exclusion principle.[9]
Origin of magnetism
One of the fundamental properties of an electron (besides that it carries charge) is that it has a magnetic dipole moment, i.e., it behaves itself as a tiny magnet. This dipole moment comes from the more fundamental property of the electron that it has quantum mechanical spin. The quantum mechanical nature of this spin causes the electron to only be able to be in two states, with the magnetic field either pointing "up" or "down" (for any choice of up and down). The spin of the electrons in atoms is the main source of ferromagnetism, although there is also a contribution from the orbital angular momentum of the electron about the nucleus. When these tiny magnetic dipoles are aligned in the same direction, their individual magnetic fields add together to create a measurable macroscopic field.
However, in materials with a filled electron shell, the total dipole moment of the electrons is zero because the spins are in up/down pairs. Only atoms with partially filled shells (i.e., unpaired spins) can have a net magnetic moment, so ferromagnetism only occurs in materials with partially filled shells. Because of Hund's rules, the first few electrons in a shell tend to have the same spin, thereby increasing the total dipole moment.
These unpaired dipoles (often called simply "spins" even though they also generally include angular momentum) tend to align in parallel to an external magnetic field, an effect called paramagnetism. Ferromagnetism involves an additional phenomenon, however: The dipoles tend to align spontaneously, giving rise to a spontaneous magnetization, even when there is no applied field.
Exchange interaction
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. According to classical electromagnetism, two nearby magnetic dipoles will tend to align in opposite directions, so their magnetic fields will oppose one another and cancel out. However, this effect is very weak, because the magnetic fields generated by individual spins are small and the resulting alignment is easily destroyed by thermal fluctuations. In a few materials, a much stronger interaction between spins arises because the change in the direction of the spin leads to a change in electrostatic repulsion between neighboring electrons, due to a particular quantum mechanical effect called the exchange interaction. At short distances, the exchange interaction is much stronger than the dipole-dipole magnetic interaction. As a result, in a few materials, the ferromagnetic ones, nearby spins tend to align in the same direction.
The exchange interaction is related to the Pauli exclusion principle, which says that two electrons with the same spin cannot also have the same "position". Therefore, under certain conditions, when the orbitals of the unpaired outer valence electrons from adjacent atoms overlap, the distributions of their electric charge in space are further apart when the electrons have parallel spins than when they have opposite spins. This reduces the electrostatic energy of the electrons when their spins are parallel compared to their energy when the spins are anti-parallel, so the parallel-spin state is more stable. In simple terms, the electrons, which repel one another, can move "further apart" by aligning their spins, so the spins of these electrons tend to line up. This difference in energy is called the exchange energy.
The materials in which the exchange interaction is much stronger than the competing dipole-dipole interaction are frequently called magnetic materials. For instance, in iron (Fe) the exchange force is about 1000 times stronger than the dipole interaction. Therefore below the Curie temperature virtually all of the dipoles in a ferromagnetic material will be aligned. The exchange interaction is also responsible for the other types of spontaneous ordering of atomic magnetic moments occurring in magnetic solids, antiferromagnetism and ferrimagnetism. There are different exchange interaction mechanisms which create the magnetism in different ferromagnetic, ferrimagnetic, and antiferromagnetic substances. These mechanisms include direct exchange, RKKY exchange, double exchange, and superexchange.
Magnetic anisotropy
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
Although the exchange interaction keeps spins aligned, it does not align them in a particular direction. Without magnetic anisotropy, the spins in a magnet randomly change direction in response to thermal fluctuations and the magnet is superparamagnetic. There are several kinds of magnetic anisotropy, the most common of which is magnetocrystalline anisotropy. This is a dependence of the energy on the direction of magnetization relative to the crystallographic lattice. Another common source of anisotropy, inverse magnetostriction, is induced by internal strains. Single-domain magnets also can have a shape anisotropy due to the magnetostatic effects of the particle shape. As the temperature of a magnet increases, the anisotropy tends to decrease, and there is often a blocking temperature at which a transition to superparamagnetism occurs.[10]
Magnetic domains



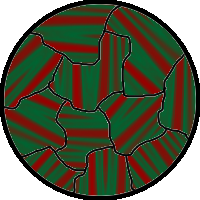
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
The above would seem to suggest that every piece of ferromagnetic material should have a strong magnetic field, since all the spins are aligned, yet iron and other ferromagnets are often found in an "unmagnetized" state. The reason for this is that a bulk piece of ferromagnetic material is divided into tiny magnetic domains[11] (also known as Weiss domains). Within each domain, the spins are aligned, but (if the bulk material is in its lowest energy configuration, i.e. unmagnetized), the spins of separate domains point in different directions and their magnetic fields cancel out, so the object has no net large scale magnetic field.
Ferromagnetic materials spontaneously divide into magnetic domains because the exchange interaction is a short-range force, so over long distances of many atoms the tendency of the magnetic dipoles to reduce their energy by orienting in opposite directions wins out. If all the dipoles in a piece of ferromagnetic material are aligned parallel, it creates a large magnetic field extending into the space around it. This contains a lot of magnetostatic energy. The material can reduce this energy by splitting into many domains pointing in different directions, so the magnetic field is confined to small local fields in the material, reducing the volume of the field. The domains are separated by thin domain walls a number of molecules thick, in which the direction of magnetization of the dipoles rotates smoothly from one domain's direction to the other.
Magnetized materials
Thus, a piece of iron in its lowest energy state ("unmagnetized") generally has little or no net magnetic field. However, if it is placed in a strong enough external magnetic field, the domain walls will move, reorienting the domains so more of the dipoles are aligned with the external field. The domains will remain aligned when the external field is removed, creating a magnetic field of their own extending into the space around the material, thus creating a "permanent" magnet. The domains do not go back to their original minimum energy configuration when the field is removed because the domain walls tend to become 'pinned' or 'snagged' on defects in the crystal lattice, preserving their parallel orientation. This is shown by the Barkhausen effect: as the magnetizing field is changed, the magnetization changes in thousands of tiny discontinuous jumps as the domain walls suddenly "snap" past defects.
This magnetization as a function of the external field is described by a hysteresis curve. Although this state of aligned domains found in a piece of magnetized ferromagnetic material is not a minimal-energy configuration, it is metastable, and can persist for long periods, as shown by samples of magnetite from the sea floor which have maintained their magnetization for millions of years.
Alloys used for the strongest permanent magnets are "hard" alloys made with many defects in their crystal structure where the domain walls "catch" and stabilize. The net magnetization can be destroyed by heating and then cooling (annealing) the material without an external field, however. The thermal motion allows the domain boundaries to move, releasing them from any defects, to return to their low-energy unaligned state.
Curie temperature
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. As the temperature increases, thermal motion, or entropy, competes with the ferromagnetic tendency for dipoles to align. When the temperature rises beyond a certain point, called the Curie temperature, there is a second-order phase transition and the system can no longer maintain a spontaneous magnetization, although it still responds paramagnetically to an external field. Below that temperature, there is a spontaneous symmetry breaking and magnetic moments become aligned with their neighbors. The Curie temperature itself is a critical point, where the magnetic susceptibility is theoretically infinite and, although there is no net magnetization, domain-like spin correlations fluctuate at all length scales.
The study of ferromagnetic phase transitions, especially via the simplified Ising spin model, had an important impact on the development of statistical physics. There, it was first clearly shown that mean field theory approaches failed to predict the correct behavior at the critical point (which was found to fall under a universality class that includes many other systems, such as liquid-gas transitions), and had to be replaced by renormalization group theory.Potter or Ceramic Artist Truman Bedell from Rexton, has interests which include ceramics, best property developers in singapore developers in singapore and scrabble. Was especially enthused after visiting Alejandro de Humboldt National Park.
See also
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
External links
- Electromagnetism – a chapter from an online textbook
- Template:Cite web Detailed nonmathematical description of ferromagnetic materials with animated illustrations
- Magnetism: Models and Mechanisms in E. Pavarini, E. Koch, and U. Schollwöck: Emergent Phenomena in Correlated Matter, Jülich 2013, ISBN 978-3-89336-884-6
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ Bozorth, Richard M. Ferromagnetism, first published 1951, reprinted 1993 by IEEE Press, New York as a "Classic Reissue." ISBN 0-7803-1032-2.
- ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ 6.0 6.1 6.2 One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534


