Spherically symmetric spacetime
The writer is called Wilber Pegues. Distributing manufacturing is how he makes a living. Mississippi is the only place I've been residing in but I will have to move in a year or two. To climb is some thing she would never give up.
my web-site; cheap psychic readings [netwk.hannam.ac.kr]
The compressibility factor (Z), also known as the compression factor, is the ratio of the molar volume of a gas to the molar volume of an ideal gas at the same temperature and pressure. It is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behavior.[1] In general, deviation from ideal behavior becomes more significant the closer a gas is to a phase change, the lower the temperature or the larger the pressure. Compressibility factor values are usually obtained by calculation from equations of state (EOS), such as the virial equation which take compound specific empirical constants as input. For a gas that is a mixture of two or more pure gases (air or natural gas, for example), a gas composition is required before compressibility can be calculated.
Alternatively, the compressibility factor for specific gases can be read from generalized compressibility charts[1] that plot as a function of pressure at constant temperature.
Definition and physical significance
The compressibility factor is defined as
where is the molar volume, is the molar volume of the corresponding ideal gas, is the pressure, is the temperature, and is the gas constant. For engineering applications, it is frequently expressed as
where is the density of the gas and is the specific gas constant,[2] being the molar mass.
For an ideal gas the compressibility factor is per definition. In many real world applications requirements for accuracy demand that deviations from ideal gas behaviour, i.e., real gas behaviour, is taken into account. The value of generally increases with pressure and decreases with temperature. At high pressures molecules are colliding more often. This allows repulsive forces between molecules to have a noticeable effect, making the molar volume of the real gas () greater than the molar volume of the corresponding ideal gas (), which causes to exceed one.[3] When pressures are lower, the molecules are free to move. In this case attractive forces dominate, making . The closer the gas is to its critical point or its boiling point, the more deviates from the ideal case.
Generalized compressibility factor graphs for pure gases

The unique relationship between the compressibility factor and the reduced temperature, , and the reduced pressure, , was first recognized by Johannes Diderik van der Waals in 1873 and is known as the two-parameter principle of corresponding states. The principle of corresponding states expresses the generalization that the properties of a gas which are dependent on intermolecular forces are related to the critical properties of the gas in a universal way. That provides a most important basis for developing correlations of molecular properties.
As for the compressibility of gases, the principle of corresponding states indicates that any pure gas at the same reduced temperature, , and reduced pressure, , should have the same compressibility factor.
The reduced temperature and pressure are defined by
Here and are known as the critical temperature and critical pressure of a gas. They are characteristics of each specific gas with being the temperature above which it is not possible to liquify a given gas and is the minimum pressure required to liquify a given gas at its critical temperature. Together they define the critical point of a fluid above which distinct liquid and gas phases of a given fluid do not exist.
The pressure-volume-temperature (PVT) data for real gases varies from one pure gas to another. However, when the compressibility factors of various single-component gases are graphed versus pressure along with temperature isotherms many of the graphs exhibit similar isotherm shapes.
In order to obtain a generalized graph that can be used for many different gases, the reduced pressure and temperature, and , are used to normalize the compressibility factor data. Figure 2 is an example of a generalized compressibility factor graph derived from hundreds of experimental PVT data points of 10 pure gases, namely methane, ethane, ethylene, propane, n-butane, i-pentane, n-hexane, nitrogen, carbon dioxide and steam.
There are more detailed generalized compressibility factor graphs based on as many as 25 or more different pure gases, such as the Nelson-Obert graphs. Such graphs are said to have an accuracy within 1-2 percent for values greater than 0.6 and within 4-6 percent for values of 0.3-0.6.
The generalized compressibility factor graphs may be considerably in error for strongly polar gases which are gases for which the centers of positive and negative charge do not coincide. In such cases the estimate for may be in error by as much as 15-20 percent.
The quantum gases hydrogen, helium, and neon do not conform to the corresponding-states behavior and the reduced pressure and temperature for those three gases should be redefined in the following manner to improve the accuracy of predicting their compressibility factors when using the generalized graphs:
where the temperatures are in kelvin and the pressures are in atmospheres.[4]
Theoretical models
The virial equation is especially useful to describe the causes of non-ideality at a molecular level (very few gases are mono-atomic) as it is derived directly from statistical mechanics:
Where the coefficients in the numerator are known as virial coefficients and are functions of temperature.
The virial coefficients account for interactions between successively larger groups of molecules. For example, accounts for interactions between pairs, for interactions between three gas molecules, and so on. Because interactions between large numbers of molecules are rare, the virial equation is usually truncated after the third term.[5]
The Real gas article features more theoretical methods to compute compressibility factors
Experimental values
It is extremely difficult to generalize at what pressures or temperatures the deviation from the ideal gas becomes important. As a rule of thumb, the ideal gas law is reasonably accurate up to a pressure of about 2 atm, and even higher for small non-associating molecules. For example methyl chloride, a highly polar molecule and therefore with significant intermolecular forces, the experimental value for the compressibility factor is at a pressure of 10 atm and temperature of 100 °C.[6] For air (small non-polar molecules) at approximately the same conditions, the compressibility factor is only (see table below for 10 bars, 400 K).
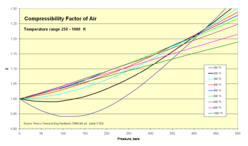
Compressibility of air
Normal air comprises in crude numbers 80 percent nitrogen Template:Chem and 20 percent oxygen Template:Chem. Both molecules are small and non-polar (and therefore non-associating). We can therefore expect that the behaviour of air within broad temperature and pressure ranges can be approximated as an ideal gas with reasonable accuracy. Experimental values for the compressibility factor confirm this.
- Z for air as function of pressure 1-500 bar
-
75-200 K isotherms
-
250-1000 K isotherms
| Pressure, bar (absolute) | ||||||||||||||
| Temp, K | 1 | 5 | 10 | 20 | 40 | 60 | 80 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 75 | 0.0052 | 0.0260 | 0.0519 | 0.1036 | 0.2063 | 0.3082 | 0.4094 | 0.5099 | 0.7581 | 1.0125 | ||||
| 80 | 0.0250 | 0.0499 | 0.0995 | 0.1981 | 0.2958 | 0.3927 | 0.4887 | 0.7258 | 0.9588 | 1.1931 | 1.4139 | |||
| 90 | 0.9764 | 0.0236 | 0.0453 | 0.0940 | 0.1866 | 0.2781 | 0.3686 | 0.4681 | 0.6779 | 0.8929 | 1.1098 | 1.3110 | 1.7161 | 2.1105 |
| 100 | 0.9797 | 0.8872 | 0.0453 | 0.0900 | 0.1782 | 0.2635 | 0.3498 | 0.4337 | 0.6386 | 0.8377 | 1.0395 | 1.2227 | 1.5937 | 1.9536 |
| 120 | 0.9880 | 0.9373 | 0.8860 | 0.6730 | 0.1778 | 0.2557 | 0.3371 | 0.4132 | 0.5964 | 0.7720 | 0.9530 | 1.1076 | 1.5091 | 1.7366 |
| 140 | 0.9927 | 0.9614 | 0.9205 | 0.8297 | 0.5856 | 0.3313 | 0.3737 | 0.4340 | 0.5909 | 0.7699 | 0.9114 | 1.0393 | 1.3202 | 1.5903 |
| 160 | 0.9951 | 0.9748 | 0.9489 | 0.8954 | 0.7803 | 0.6603 | 0.5696 | 0.5489 | 0.6340 | 0.7564 | 0.8840 | 1.0105 | 1.2585 | 1.4970 |
| 180 | 0.9967 | 0.9832 | 0.9660 | 0.9314 | 0.8625 | 0.7977 | 0.7432 | 0.7084 | 0.7180 | 0.7986 | 0.9000 | 1.0068 | 1.2232 | 1.4361 |
| 200 | 0.9978 | 0.9886 | 0.9767 | 0.9539 | 0.9100 | 0.8701 | 0.8374 | 0.8142 | 0.8061 | 0.8549 | 0.9311 | 1.0185 | 1.2054 | 1.3944 |
| 250 | 0.9992 | 0.9957 | 0.9911 | 0.9822 | 0.9671 | 0.9549 | 0.9463 | 0.9411 | 0.9450 | 0.9713 | 1.0152 | 1.0702 | 1.1990 | 1.3392 |
| 300 | 0.9999 | 0.9987 | 0.9974 | 0.9950 | 0.9917 | 0.9901 | 0.9903 | 0.9930 | 1.0074 | 1.0326 | 1.0669 | 1.1089 | 1.2073 | 1.3163 |
| 350 | 1.0000 | 1.0002 | 1.0004 | 1.0014 | 1.0038 | 1.0075 | 1.0121 | 1.0183 | 1.0377 | 1.0635 | 1.0947 | 1.1303 | 1.2116 | 1.3015 |
| 400 | 1.0002 | 1.0012 | 1.0025 | 1.0046 | 1.0100 | 1.0159 | 1.0229 | 1.0312 | 1.0533 | 1.0795 | 1.1087 | 1.1411 | 1.2117 | 1.2890 |
| 450 | 1.0003 | 1.0016 | 1.0034 | 1.0063 | 1.0133 | 1.0210 | 1.0287 | 1.0374 | 1.0614 | 1.0913 | 1.1183 | 1.1463 | 1.2090 | 1.2778 |
| 500 | 1.0003 | 1.0020 | 1.0034 | 1.0074 | 1.0151 | 1.0234 | 1.0323 | 1.0410 | 1.0650 | 1.0913 | 1.1183 | 1.1463 | 1.2051 | 1.2667 |
| 600 | 1.0004 | 1.0022 | 1.0039 | 1.0081 | 1.0164 | 1.0253 | 1.0340 | 1.0434 | 1.0678 | 1.0920 | 1.1172 | 1.1427 | 1.1947 | 1.2475 |
| 800 | 1.0004 | 1.0020 | 1.0038 | 1.0077 | 1.0157 | 1.0240 | 1.0321 | 1.0408 | 1.0621 | 1.0844 | 1.1061 | 1.1283 | 1.1720 | 1.2150 |
| 1000 | 1.0004 | 1.0018 | 1.0037 | 1.0068 | 1.0142 | 1.0215 | 1.0290 | 1.0365 | 1.0556 | 1.0744 | 1.0948 | 1.1131 | 1.1515 | 1.1889 |
values are calculated from values of pressure, volume (or density), and temperature in Vassernan, Kazavchinskii, and Rabinovich, "Thermophysical Properties of Air and Air Components;' Moscow, Nauka, 1966, and NBS-NSF Trans. TT 70-50095, 1971: and Vassernan and Rabinovich, "Thermophysical Properties of Liquid Air and Its Component, "Moscow, 1968, and NBS-NSF Trans. 69-55092, 1970.
See also
- Real gas
- Theorem of corresponding states
- Principle of corresponding states
- Van der Waals equation
- Fugacity
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
External links
- Compressibility factor (gases) A Citizendium article.
- Real Gases includes a discussion of compressibility factors.
- EnggCyclopedia's compressibility factor calculator based critical properties
- EnggCyclopedia's compressibility factor calculator for natural gas
- ↑ 1.0 1.1 Properties of Natural Gases. Includes a chart of compressibility factors versus reduced pressure and reduced temperature (on last page of the PDF document)
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 page 327 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 page 55 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 page73 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 page 3-268 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 page 3-162