Erdős–Szemerédi theorem

Ring lasers with a perimeter larger than about 40 cm ("large" ring lasers) are extremely precise instruments capable of measuring phenomena in optics and gravitation such as details of Earth rotation, Fresnel drag, Lense-Thirring effect, gravitational waves, quantum-electrodynamic effects and other relativistic effects. A 243-day measurement involving a 16 m ring yielded the greatest resolution achieved so far by any known measurement device.

Construction

Ring lasers are composed of two beams of light of the same polarization traveling in opposite directions ("counter-rotating") in a closed loop. In large ring lasers, this loop is usually square (figure 1). Mirrors are used to focus and redirect the beams at the corners. While traveling between mirrors, the beams pass through gas-filled tubes. The beams are generated through local excitation of the gas by radio frequencies.

Critical variables in the construction of a large ring laser with a high quality factor (which ensures a high signal-to-noise ratio) include:

• Size: Larger ring lasers can measure lower frequencies. The sensitivity of large rings increases quadratically with size.
• Mirrors: Reflectivities of not less than 99.999% are required for high-quality rings. Mirrors must also be sufficiently large to reflect virtually all of the incident beam power.
• Stability: The assembly must be attached to or built within a substance that is extremely insensitive to temperature changes (e.g. Zerodur, or bedrock for extremely large rings).
• Gas: HeNe generates beams with the most desirable features.

History

Shortly after the discovery of the laser, a seminal paper by Rosenthal appeared in 1962, which proposed what was later called a ring laser. While the ring laser shares with regular (linear) lasers features like extreme monochromaticity and high directivity, it differs in its inclusion of an area. With the ring laser, one could distinguish two beams in opposite directions. Rosenthal anticipated that the beam frequencies could be split by effects that affected the two beams in different ways. Macek et al. built the first large ring laser (1 meter x 1 meter) and showed that simply rotating it could generate a difference in the frequencies of the two beams ( Sagnac). An industry focusing on smaller ring laser gyros emerged, with decimeter-sized ring lasers. Later it was found that any effect that affects the two beams in nonreciprocal fashion produces a frequency difference as Rosenthal anticipated. Tools to analyze and construct rings were adapted from regular lasers, including methods to calculate the signal-to-noise ratio and to analyze beam characteristics. New phenomena unique to rings appeared, including lock-in, pulling, astigmatic beams, and special polarizations. Mirrors play a much greater role in ring lasers than in linear lasers, leading to the development of particularly high quality mirrors.

Table 1. ~108 improvement in the resolution of large rings from 1972 to 2004.

year	rms linewidth	measurement time	source
1972	4.5 Hz	10 s	Stowell
1993	68 mHz	16 s	Bilger
1994	31 mHz	8 h	Stedman
1995	8.6 µHz	8 d	Bilger
2004	50 nHz	243 d	Screiber

The resolution of large ring lasers has dramatically improved, as a result of a 1000-fold improvement in the quality factor (see Table 1). This improvement is largely a result of the removal of interfaces that the beams need to traverse. A 1 m x 1 m ring built in Christchurch, New Zealand in 1992 was sensitive enough to measure the Earth's rotation (figure 2), and a 4 m x 4 m ring built in Wettzell, Germany improved the precision of this measurement to six digits (figure 1).

Figure 2. The Canterbury ring.

Definition of large rings

Ring Lasers are laser systems where the lasing encloses an area, as opposed to linear lasers. They measure any rotation present at their locations (Sagnac effect ), which found an early application as gyros in moving vessels like cars, ships, planes, and missiles. Most ring lasers employ two counterrotating optical monomode beams. The perimeter dependence of the Signal/Noise ratio is

${\text{ }}S/N\propto L^{3}[1-e^{-({\frac {L_{crit}}{L}})^{2}}]^{\frac {1}{2}}$

This equation defines large rings with L >> L_crit ≈ 40 cm, where S/N becomes proportional to L². Therefore the sensitivity of large rings increases quadratically with size, hence the quest for ever larger rings.

In the past it was thought that only small ring lasers avoid multimode excitation. However, if signal bandwidth is sacrificed, there is no known limit to ring laser size, either theoretically or experimentally.

The response to a rotation is a frequency difference Δfs between the two beams (typically, the HeNe lasing gas at 633 nm is used; attempts for an argon ring laser failed ), which is proportional to the rotation rate of the ring laser (Sagnac effect). The difference can easily be measured.

Signal and noise

The following equations can be used to calculate the signal-to-noise ratio, S/N for rotation.

The signal frequency is

S = Δfs = 4${\frac {{\vec {\Omega }}\cdot {\vec {A}}}{\lambda L}}$,

where ${\vec {A}}$ is the area vector, ${\vec {\Omega }}$ is the rotation rate vector, λ is the vacuum wavelength, L is the perimeter. (For complicated geometries like nonplanar rings or figure-8 rings, the definitions

${\vec {A}}={\frac {1}{2}}\oint {{\vec {r}}\times }d{\vec {l}}$ and L = $\oint {dl}$ are to be used.)

The noise frequencies are

N = $S_{\delta f}={\frac {hf^{3}}{PQ^{2}}}$,

where $S_{\delta f}$ is the power spectral density of quantum noise, h is Planck’s constant, f is the laser frequency, P includes all power losses of the laser beams, and Q is the quality factor of the ring.

Beam characteristics: curvature radius, width, and polarization

A beam mode in rings is typically a gaussian with a spot size w: $\left|E\right|=\left|E_{0}\right|e^{-{\frac {r^{2}}{w^{2}}}}$,

where $E_{0}$ is the peak field of the beam, E is the field distribution, and r is the distance off beam center.

The mirror sizes have to be chosen large enough to ensure that only very small portions of the gaussian tails are to be cut off, such that the calculated Q (below) is maintained.

The phase is spherical with radius of curvature R. The analysis of these characteristics is presented in the Wiki article Ring laser. Further analyses are given in the following references:, and. The major results of the matrix calculations, given the roundtrip matrix ABCD, are:

$\left|{\begin{matrix}A&B\\C&D\\\end{matrix}}\right|=1$

and

$\left|{\frac {A+D}{2}}\right|\leq 1$ .

The polarization of rings exhibits particular features: Planar rings are theoretically either s-polarized, i.e. perpendicular to the ring plane, or p-polarized, in the plane; non-planar rings are circularly polarized. A planar ring, however, is invariably s-polarized because the losses of the multilayer mirrors used are always less in s-polarized beams (at the so-called “Brewster angle”, the reflected p-component even vanishes).

Quality factor

It is quite important for large rings to increase the quality factor Q, because it appears as 1/Q² in the expression for noise.

Definition: $Q=2\pi f_{0}{\frac {W}{-{\frac {dW}{dt}}}}$. Since the operating frequency $f_{0}$ of the ring is given (474 THz), it remains to increase the circulating energy in the ring W and decrease the power losses dW/dt as much as possible. W is obviously proportional to the length of the ring, but must be limited to avoid multimodes. The power losses dW/dt however can be vastly decreased. The ensuing decreased signal output power is not critical, as modern silicon detectors have low noise, and for very low signals photomultipliers are used.

The power loss can be minimized by increasing the reflectivity of the mirrors to as close to 1 as possible and by eliminating other, spurious, sources of power loss, for example the inaccuracy of mirror curvature. Any interfaces or apertures that would decrease the quality factor of the ring are avoided. The whole ring is filled with a HeNe mixture of suitable partial pressures (up to a few hundred Pascal), to achieve lasing and good suppression of multiple pairs of modes. Further, the lasing is excited with radio frequency to easily adjust the amplitude to just below the appearance of the second pair of modes. The Rayleigh scattering of the HeNe gas is, at this time, negligible.

For mirrors of proper curvature (spherical shape is acceptable) and equal reflectances r, the quality factor is

$Q={\frac {\pi L}{2\lambda (1-r)}}$.

This equation gives rise to formidable quality factors. For a 4 m x 4 m ring equipped with 1 ppm mirrors (R = 1-10⁻⁶) we would get, at 474 THz, Q = 4×10¹³. This quality factor produces a passive resonance line of rms = 5 Hz, which is eight orders of magnitude smaller than the atomic linewidth of the Ne line (a 1:1 mixture of the two isotopes Ne²⁰ and Ne²² has a gain bandwidth of about 2.2 GHz). (Note that for example in regular pendulums the Q is of the order of 10³ and in wristwatch-type quartzes it is of the order of 10⁶.) The active ring further reduces the linewidth by several orders of magnitude, and increasing the measuring time may additionally decrease the linewidth by many orders of magnitude.

Measurement of Q

The integral of the definition equation for Q above is: $W=W_{0}e^{-{\frac {\omega t}{Q}}}\equiv W_{0}e^{-{\frac {t}{\tau }}}$ (τ is the photon lifetime.) Thus, Q = ωτ. This is an extremely simple equation to measure Q in large rings. The photon lifetime τ is measured on an oscilloscope, as the times are of the order of microseconds to milliseconds.

Shape of rings

In order to maximize the signal/noise ratio of a ring inside a given circle of radius r with n mirrors, a planar ring is advantageous over an equivalent nonplanar ring. Furthermore, a regular polygon has a maximal A/Ln ratio, with A/Ln = ${\frac {r}{2}}{\frac {\cos(\pi /n)}{n}}$ which itself has a maximum at n = 4, hence a planar square ring is optimal.

Lock-in and pulling

One advantage of large rings over smaller rings is a significant reduction in the lock-in frequency f_L, which is the frequency at which the difference between the beam frequencies becomes so small that it collapses, synchronizing the two counterrotating beams. Generally, if the theoretical frequency difference is f_t, the actual signal frequency f is

$f=f_{t}{\sqrt {1-({\frac {f_{L}}{f_{t}}})^{2}}}$. This equation says that even slightly above lock-in, there is already a reduction in frequency (i.e. pulling) relative to the theoretical frequency. When the dependence on perimeter L is taken into account for large rings, the relative difference between theoretical output frequency f_t and actual output frequency f is inversely proportional to the fourth power of L:

${\frac {f_{t}-f}{f_{t}}}\cong {\frac {1}{2}}({\frac {f_{L}}{f_{t}}})^{2}\propto {\frac {1}{L^{4}}}$. This is a huge advantage of large rings over small ones. As an example, small navigational gyros have lock-in frequencies on the order of 1 kHz. The first large ring had a lock-in frequency of about 2 kHz, and the first ring that could measure the Earth’s rotation rate had a lock-in frequency of about 20 Hz. This ring was constructed in 1992 by a group from Canterbury University at Christchurch, New Zealand, and Oklahoma State University, see figure 2. The square ring is mounted on a Zerodur plate. The four mirrors are housed in stainless steel boxes and placed on the Zerodur.

Figure 3. An early spectrum obtained when the Canterbury ring was housed in a building.

Figure 3 shows one of the early spectra obtained while the ring of figure 2 was still mounted on the seventh floor of a building. It shows the Earth line (c), the 50 Hz power line frequency (a) (50 Hz in New Zealand) and its harmonic (e) at 100 Hz, besides massive “building noise” (b,d). The latter is symmetric to the Earth line (Bessel functions J₁ and J_-1). Figure 4 shows a spectrum obtained after 25 s of measurement, at a sampling rate r = 500/s, when the ring was placed 30 m underground in a cave. The lines E₁ to E₄ are harmonics of the response to Earth rotation with the predicted geometrical power decay ( ${\bar {E}}_{4}$ is aliased), together with two even harmonics of the power line frequency M₂ and M₄. Note the essential absence, on this scale, of any other noises, in particular of building noises. The difference relative to figure 3 is evident. The linewidth of E₁ happened to be smaller than that of the New Zealand power line frequency!

Figure 4. High resolution spectrum obtained when the Canterbury ring was housed underground.

Grossring

A square ring of size 4 m x 4 m (“Grossring”, figure 1) working in Wettzell, Germany, is close to its theoretical resolution. The Earth rotation created a measured output of 348.635 Hz, whereas the theoretical frequency was 348.529 Hz. Its lock-in frequency is well below 1 Hz. It is constructed entirely with low-expansion Zerodur (thermal expansion coefficient 1.0×10⁻⁸ K⁻¹), and housed underground to eliminate building noise and to enhance its thermal stability, in particular to reduce daily and seasonal ambient temperature fluctuations in view of long term measurements (over several months). In figure 1, the four Zerodur beams are mounted on a 4.25 m-diameter Zerodur dish. They support the mirrors at the ends. Stainless steel tubes carrying the laser are connected via bellows to the Zerodur. The radio frequency excitation electrodes are applied to the Pyrex tube mounted in the center of the tube at right. The filling/pumping station is on the tube at left.

Geodetic effects

Large rings are able to measure Earth movements to very high resolution. As an example, the Grossring, which was specifically designed to measure Earth movements, was able to measure the Earth wobble. Large rings are very sensitive to seismographic effects.

Seismography

Ring lasers are complementary to standard seismometers. There are at least two phenomena by which seismic events can cause a ring signal:

1. Seismic waves that cause an instantaneous rotation, which adds to or subtracts from the Earth rotation; This is inherent in Rayleigh waves with a horizontal direction of the curl vector and in Love waves with a vertical direction of the curl vector

2. A change of the position of the vector ${\vec {A}}$. In the New Zealand rings, Ocean effects (waves) are routinely measured in the frequency range 0.1 – 1 Hz. Regular Earthquakes produce spikes whose onset can be detected with millisecond accuracy, as the signal from a Philippine Earthquake shows at the Grossring, 10,040 km away, in figure 6. With the great sensitivities displayed, it may be possible (with autocorrelation techniques) to find precursors, and to install an early warning system.

Figure 6. Detection of a Philippine earthquake by the Grossring in Wettzell, Germany — 10,040 km away.

Earth wobble

The Grossring, together with two other ringlasers, was able to measure the daily Earth wobble, where the Earth axis moves in a double cone. The wobble lines appear as side lobes (figure 5), with the two major components 10.754 μHz and 11.665 μHz off the ringlaser output at 348.635 Hz due to the sidereal Earth rotation rate of 11.606 μHz. The largest wobble mode is calculated to have a radius of 0.2685 m (≈1 foot) at the North Pole. The outputs produced by the Earth rotation rate and its wobble are in such proximity that several months of measurement are required to separate the two types of signals. The rms-width of the wobble lines after 95 days was 180 nHz (drift was analytically removed). The relative resolution of the beam frequency (λ = 633 nm corresponds to 473.6 THz) was thus

180 nHz/ 473.6THz = 4 x 10⁻²². The separation of the peaks is still 1 - 2 orders of magnitude more precise.

To increase this extraordinary resolution further, measurements of up to 243 days were made. This long measurement time was itself responsible for the majority, 122 nHz (Full width at half maximum) of the total linewidth. In the Grossring run shown in figure 5, the rms error of the precision was 50 nHz. This is the greatest resolution achieved so far by any known measurement device.

Figure 5. Grossring spectrum (of wobble), 243 days - 6/24/2002-3/26/2003; Tage = days; Frequenz = frequency

Figure 5 shows the results of this run on the Grossring. The Earth line is eliminated. An estimate of the time window itself is 42 nHz rms. The total indicated rms spread is 50 nHz.

A still larger rectangular ring was constructed by the group from Canterbury University in a cave near Christchurch, with a perimeter of 121.4 m and a 4.3 times larger A/L. It is working, but its performance is substantially below its prediction. This was caused by errors of mirror curvature of the order of 10 nm, although the basic reflection losses are still in the parts per million range. The theoretical resolution is of the order of 10⁻¹⁰ of the Earth rotation rate, which is in the range of resolution where all kinds of relativity and gravitational effects can be measured, besides many optical effects. A small selection of such effects is described below in the chapter Future Topics.

A practical limitation of sensitivity for earthbound ring lasers is given by the fact that the Earth rotation has fluctuations containing both random and single frequency components below 10⁻⁸ of the Earth rotation, which makes them easy to detect but makes detection of less pronounced effects more difficult.

Special Relativity Effects

Ring lasers constitute a new measurement tool for measuring special relativity effects, opening up a whole new set of possible experiments. A classic example is the study of Fresnel drag, which describes the impact of moving material on the velocity of light.

In special relativity, changing the frame of reference creates new phenomena. These phenomena, such as the de Sitter precession and the Thomas rotation (and many others), can be measured with ring lasers.

Fresnel drag

This is a classic phenomenon which was first tackled by Fresnel in 1818, and received various treatments during the last two centuries. The ring laser is a tool par excellence to arrive at precision measurements of this effect, as drag acts nonreciprocally on the two beams.

When light travels through material moving with velocity v, how much of v is imparted on the light? It has to be a fraction because the total light velocity can never exceed the vacuum light velocity c = 3.00 x 10⁸ m/s. The answer at present is αv with $\alpha =1-1/n^{2}-(\lambda /n)(dn/d\lambda )$ for the Macek and the Bilger arrangements (Lorentz drag; Fresnel arrived at the first two terms on the right with a mechanical model). They used a rotating quartz disc that was inserted tilted at the Brewster angle and with the beam off-axis. By changing the off-axis distance and the rotation rate, the component of the disc velocity could be varied in a wide range. For the 633 nm laser in fused quartz, Macek et al. verified the first two terms. Bilger and Stowell measured α = 0.5424 ± 0.0002, while the theoretical result was 0.54182. They verified the existence of the dispersion term in the above equation. The reason for the residual discrepancy is unknown.

Future topics

General ideas

With sensitivities of better than 10⁻²² already reached, there is a whole gamut of novel experiments within reach. Because a large ring is such a high-resolution instrument, new discoveries are possible that are not foreseen by theory.

Below is a survey of a few possibilities and suggested procedures to attain them. Some of the proposed experiments are of long standing.

As shown above, earthbound rings will show mainly fluctuations of the Earth rotation vector (that is why the definition of the day by the Earth rotation was rejected long ago), and these fluctuations constitute “noise” in the context of projects designed to measure different effects. However, there are ways to compensate for this drawback and for the deficiencies of the instrument.

I. Since any drift of machine, earth rotation rate, signal detection electronics etc. contains extremely low Fourier frequencies, it can be removed analytically by Hilbert domain techniques. (The “drift” has frequencies well below 1 Hertz, whereas the Sagnac line of the Earth rotation and its satellites, as well as Earth quake measurements, gravitational waves, etc. have information at the level of 100 Hz or higher). In this fashion, the drift of the Sagnac line is removed, in order to get to the true line shape without drift.

II. To observe satellites to the (slightly drifting) Sagnac line, one measures the frequency distribution of the satellite pattern with the Sagnac line as a frequency reference. This difference has no drift. A second order autocorrelation technique has been used to establish the satellite pattern. This was for example done to measure the wobble.

III. To reduce noise when measuring effects that can be reversed, the length of the intervals between reversals should minimize the Allan variance. Reversals double the frequency difference generated by the effect.

There is however a caveat in many of these planned experiments: lines at low frequencies (in the microhertz region for example) require lengthy measurement times. In the simplest case, a gaussian-distributed line with rms width σ(ω) requires a gaussian-distributed time window σ(t) such that

σ(ω) · σ(t) = 1. With different shapes of time windows and line shapes this relation has an increased numerical right side. To achieve an rms frequency line width of 10 nHz e.g., the rms time window needs to be at least about 6 months, i.e. one needs a time series of several years.

The wobble spectrum in figure 5 produced lines with rms-widths of 50 nHz after 243 days (21x10⁶ s). Generally, a line in the neighborhood of 1 μHz needs months to establish. Table I shows the progress in resolution done by the German-New Zealand-Oklahoma group in reducing linewidth.

Quantum-electrodynamic effect

In classical EM theory there is no interaction. However in Quantum Electrodynamics (QED), Denisov calculated that with sufficiently strong magnetic fields, as for example provided by superconducting magnets along the beam, a nonreciprocal frequency shift ought to be observable with sufficiently sensitive rings. Since sidelines with a few microhertz separation and three orders of magnitude lower amplitudes than the Sagnac line have been observed, it stands to reason that there is a chance to observe such a QED effect. The following provisos need to be acted upon:

1. Of utmost importance is the supply of a sufficiently strong magnetic field ${\vec {B}}$ over a reasonable portion of the beam path.

2. One should be able to switch the field on and off, or better, reverse it, in order to measure the spectrum with reversed polarizations of ${\vec {B}}$.

3. The duration of one polarization should be of the order of the time where the minimum of the Allan variance occurs. This is at this time about 1000 s, but one expects possibly orders of magnitude longer times with improving stability of the rings, as any 1/f etc. noise may be substantially reduced with better constructed rings.

4. Of particular importance is a careful shielding of the plasma, which is very sensitive to magnetic fields.

Gravitational wave antenna

A figure-8 ring as a gravitational detector has been proposed, figure 7.

Figure 7. Proposed gravitational wave detector.

The spacing between the mirrors is λ/2 (λ would be the wavelength of a gravitational wave). The wave would effect a rotation of the upper triangle in one sense and a rotation of the lower triangle in the opposite sense, thus effectively producing a ring signal. The size, of order of km, presents in principle no obstacle.

Terrestrial Lense-Thirring (LT) effect

A rotating mass introduces an additional gravitational field to the standard Newton gravitational field. With a spherically symmetric mass (Earth), the additional angular rotation vector is

${\vec {\Omega }}'={\frac {G\cdot I}{c^{2}\cdot R_{E}^{3}}}\left[3{\frac {{\vec {\Omega }}\bullet {\vec {R}}_{E}}{R_{E}^{2}}}\cdot {\vec {R}}_{E}-{\vec {\Omega }}\right]$

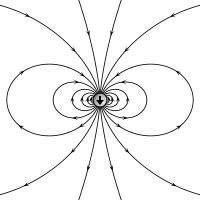
G = Newton’s gravitational constant = 6.7x10⁻¹¹ m³/ s²kg, I = moment of inertia of Earth = 8.0x10³⁷ kgm², R_E = the mean Earth radius = 6.37x10⁶ m (for rings on the Earth surface), Ω = 7.29x10⁻⁵ rad/s, c = vacuum velocity of light = 3.00x10⁸ m/s, ${\vec {R}}_{E}$ = distance vector of detector from Earth center. The LT effect has the same coordinate-free form as the field of an electric dipole.

Figure 8. Lense-Thirring gravitational field of rotating Earth.

The cofactor a = ${\frac {G\cdot I}{c^{2}\cdot R_{E}^{3}}}$ = 2.3 x10⁻¹⁰ is extremely small while the bracket is of order Ω. Therefore the Sagnac effect of the LT rotation is about 10 orders of magnitude less than the Sagnac effect of the Earth rotation. The vector ${\vec {\Omega }}^{'}$ generally shows in a different direction than ${\vec {\Omega }}$. The LT field is maximal at the two poles but not zero at the equator.

A placement of an ultrahigh-precision large ring to eliminate the Earth’s Sagnac effect such that ${\vec {A}}\bot {\vec {\Omega }}$ has been suggested. In this case the ring’s LT output is

$\Delta f=6{\frac {\Omega A}{\lambda L}}a\sin 2\theta$, θ = latitude i.e. the ring’s LT output would be 0 at the poles and at the equator, and maximum at 45° latitude, where the LT component parallel to the ring's area vector is maximal.

As such the suggestion is impractical, as an accuracy of 10⁻¹⁰ of placement is required. A slight modification of this proposal is the following: A ring of about 10 m x 10 m is placed as close as possible to ${\vec {A}}\bot {\vec {\Omega }}$. The North and South mirrors are on a meridian and are synchronously rotatable so that the laser beam can be tilted to effect a slight change of the direction of ${\vec {A}}$ such that it goes through the position ${\vec {A}}\bot {\vec {\Omega }}$ without changing A. With proper tuning the Earth line will vanish but the LT line will establish itself over the following months, corresponding to 2π rotation in about 2 billion years! The final adjustment may have to be done with piezoelements, a technique which is quite familiar in the gyro industry. The condition ${\vec {A}}\bot {\vec {\Omega }}$ can be maintained by minimizing the ringlaser output with a feedback circuit that controls the mirror positions. This latter approach is advantageous over an older suggestion to lock the ring’s attitude to the stars. Numerically, a 10 m x 10 m ring should produce an LT output of 1.06 μHz at 45° latitude. which would take measuring times of the order of several months.

To avoid lock-in:

I. The simplest approach may be not to put ${\vec {A}}$ exactly perpendicular to ${\vec {\Omega }}$but to leave enough regular Sagnac effect in to avoid lock-in.

II. A magnetic field can be applied to the plasma, parallel (and antiparallel) to the counterrotating beams. This is known to bias the beams. Furthermore, an ac magnetic field can be superimposed whose frequency is chosen such that the LT effect is placed in a "clean" spot of the ring output spectrum vis-à-vis Earth rotation fluctuations, microseisms, ocean tides, etc.

III. An additional experimental trick would be to sinusoidally rotate the N - S mirrors around horizontal axes (akin to dithering), creating additional satellites, in order to separate further residual Earth rotation and the LT. effect.

IV. It may also be possible to have counterrotating beams with circular polarization of different handedness.

V. An artificial sinusoidal oscillator could be inserted to serve as a reference in the spectrum.

The choice among these options depends largely on the size of the 1/f noise

Most of the suggested approaches can be tried with a ring that is flat on Earth. To improve on the measuring time because of the smallness of ${\vec {\Omega }}^{'}$, much larger rings with correspondingly more sensitivity could be installed. The placement of a 100 m x 100 m ring underground at a tilt of, for example, 45° would constitute a major engineering feat.

References

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.