Compressed air energy storage

The short-time Fourier transform (STFT), or alternatively short-term Fourier transform, is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time.

STFT

Continuous-time STFT

Simply, in the continuous-time case, the function to be transformed is multiplied by a window function which is nonzero for only a short period of time. The Fourier transform (a one-dimensional function) of the resulting signal is taken as the window is slid along the time axis, resulting in a two-dimensional representation of the signal. Mathematically, this is written as:

$\mathbf {STFT} \{x(t)\}(\tau ,\omega )\equiv X(\tau ,\omega )=\int _{-\infty }^{\infty }x(t)w(t-\tau )e^{-j\omega t}\,dt$

where w(t) is the window function, commonly a Hann window or Gaussian window bell centered around zero, and x(t) is the signal to be transformed. X(τ,ω) is essentially the Fourier Transform of x(t)w(t-τ), a complex function representing the phase and magnitude of the signal over time and frequency. Often phase unwrapping is employed along either or both the time axis, τ, and frequency axis, ω, to suppress any jump discontinuity of the phase result of the STFT. The time index τ is normally considered to be "slow" time and usually not expressed in as high resolution as time t.

Discrete-time STFT

DTZ's public sale group in Singapore auctions all forms of residential, workplace and retail properties, outlets, homes, lodges, boarding homes, industrial buildings and development websites. Auctions are at present held as soon as a month.

We will not only get you a property at a rock-backside price but also in an space that you've got longed for. You simply must chill out back after giving us the accountability. We will assure you 100% satisfaction. Since we now have been working in the Singapore actual property market for a very long time, we know the place you may get the best property at the right price. You will also be extremely benefited by choosing us, as we may even let you know about the precise time to invest in the Singapore actual property market.

The Hexacube is offering new ec launch singapore business property for sale Singapore investors want to contemplate. Residents of the realm will likely appreciate that they'll customize the business area that they wish to purchase as properly. This venture represents one of the crucial expansive buildings offered in Singapore up to now. Many investors will possible want to try how they will customise the property that they do determine to buy by means of here. This location has offered folks the prospect that they should understand extra about how this course of can work as well.

Singapore has been beckoning to traders ever since the value of properties in Singapore started sky rocketing just a few years again. Many businesses have their places of work in Singapore and prefer to own their own workplace area within the country once they decide to have a everlasting office. Rentals in Singapore in the corporate sector can make sense for some time until a business has discovered a agency footing. Finding Commercial Property Singapore takes a variety of time and effort but might be very rewarding in the long term.

is changing into a rising pattern among Singaporeans as the standard of living is increasing over time and more Singaporeans have abundance of capital to invest on properties. Investing in the personal properties in Singapore I would like to applaud you for arising with such a book which covers the secrets and techniques and tips of among the profitable Singapore property buyers. I believe many novice investors will profit quite a bit from studying and making use of some of the tips shared by the gurus." – Woo Chee Hoe Special bonus for consumers of Secrets of Singapore Property Gurus Actually, I can't consider one other resource on the market that teaches you all the points above about Singapore property at such a low value. Can you? Condominium For Sale (D09) – Yong An Park For Lease

In 12 months 2013, c ommercial retails, shoebox residences and mass market properties continued to be the celebrities of the property market. Models are snapped up in report time and at document breaking prices. Builders are having fun with overwhelming demand and patrons need more. We feel that these segments of the property market are booming is a repercussion of the property cooling measures no.6 and no. 7. With additional buyer's stamp responsibility imposed on residential properties, buyers change their focus to commercial and industrial properties. I imagine every property purchasers need their property funding to understand in value. In the discrete time case, the data to be transformed could be broken up into chunks or frames (which usually overlap each other, to reduce artifacts at the boundary). Each chunk is Fourier transformed, and the complex result is added to a matrix, which records magnitude and phase for each point in time and frequency. This can be expressed as:

$\mathbf {STFT} \{x[n]\}(m,\omega )\equiv X(m,\omega )=\sum _{n=-\infty }^{\infty }x[n]w[n-m]e^{-j\omega n}$

likewise, with signal x[n] and window w[n]. In this case, m is discrete and ω is continuous, but in most typical applications the STFT is performed on a computer using the Fast Fourier Transform, so both variables are discrete and quantized.

The magnitude squared of the STFT yields the spectrogram of the function:

$\operatorname {spectrogram} \{x(t)\}(\tau ,\omega )\equiv |X(\tau ,\omega )|^{2}$

See also the modified discrete cosine transform (MDCT), which is also a Fourier-related transform that uses overlapping windows.

Sliding DFT

If only a small number of ω are desired, or if the STFT is desired to be evaluated for every shift m of the window, then the STFT may be more efficiently evaluated using a sliding DFT algorithm.

Inverse STFT

The STFT is invertible, that is, the original signal can be recovered from the transform by the Inverse STFT. The most widely accepted way of inverting the STFT is by using the overlap-add (OLA) method, which also allows for modifications to the STFT complex spectrum. This makes for a versatile signal processing method, referred to as the overlap and add with modifications method.

Continuous-time STFT

Given the width and definition of the window function w(t), we initially require the area of the window function to be scaled so that

$\int _{-\infty }^{\infty }w(\tau )\,d\tau =1.$

It easily follows that

$\int _{-\infty }^{\infty }w(t-\tau )\,d\tau =1\quad \forall \ t$

and

$x(t)=x(t)\int _{-\infty }^{\infty }w(t-\tau )\,d\tau =\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau .$

The continuous Fourier Transform is

$X(\omega )=\int _{-\infty }^{\infty }x(t)e^{-j\omega t}\,dt.$

Substituting x(t) from above:

$X(\omega )=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau \right]\,e^{-j\omega t}\,dt$

$=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,d\tau \,dt.$

Swapping order of integration:

$X(\omega )=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,dt\,d\tau$

$=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,dt\right]\,d\tau$

$=\int _{-\infty }^{\infty }X(\tau ,\omega )\,d\tau .$

So the Fourier Transform can be seen as a sort of phase coherent sum of all of the STFTs of x(t). Since the inverse Fourier transform is

$x(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\omega )e^{+j\omega t}\,d\omega ,$

then x(t) can be recovered from X(τ,ω) as

$x(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\tau \,d\omega .$

or

$x(t)=\int _{-\infty }^{\infty }\left[{\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\omega \right]\,d\tau .$

It can be seen, comparing to above that windowed "grain" or "wavelet" of x(t) is

$x(t)w(t-\tau )={\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\omega .$

the inverse Fourier transform of X(τ,ω) for τ fixed.

Resolution issues

One of the downfalls of the STFT is that it has a fixed resolution. The width of the windowing function relates to how the signal is represented—it determines whether there is good frequency resolution (frequency components close together can be separated) or good time resolution (the time at which frequencies change). A wide window gives better frequency resolution but poor time resolution. A narrower window gives good time resolution but poor frequency resolution. These are called narrowband and wideband transforms, respectively.

Comparison of STFT resolution. Left has better time resolution, and right has better frequency resolution.

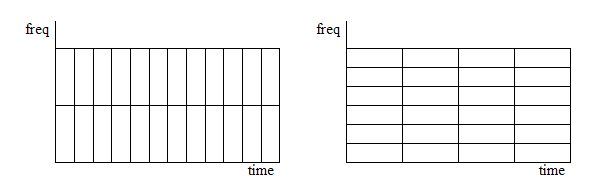
This is one of the reasons for the creation of the wavelet transform and multiresolution analysis, which can give good time resolution for high-frequency events, and good frequency resolution for low-frequency events, which is the type of analysis best suited for many real signals.

This property is related to the Heisenberg uncertainty principle, but it is not a direct relationship – see Gabor limit for discussion. The product of the standard deviation in time and frequency is limited. The boundary of the uncertainty principle (best simultaneous resolution of both) is reached with a Gaussian window function, as the Gaussian minimizes the Fourier uncertainty principle. This is called the Gabor transform (and with modifications for multiresolution becomes the Morlet wavelet transform).

One can consider the STFT for varying window size as a two-dimensional domain (time and frequency), as illustrated in the example below, which can be calculated by varying the window size. However, this is no longer a strictly time–frequency representation – the kernel is not constant over the entire signal.

Example

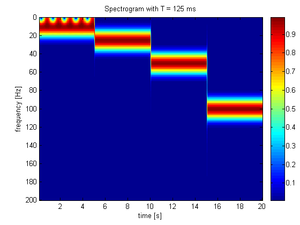
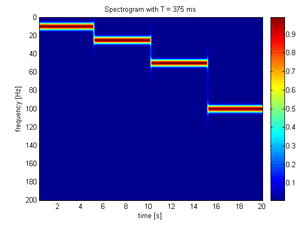
Using the following sample signal $x(t)$ that is composed of a set of four sinusoidal waveforms joined together in sequence. Each waveform is only composed of one of four frequencies (10, 25, 50, 100 Hz). The definition of $x(t)$ is:

$x(t)={\begin{cases}\cos(2\pi 10t/\mathrm {s} )&0\,\mathrm {s} \leq t<5\,\mathrm {s} \\\cos(2\pi 25t/\mathrm {s} )&5\,\mathrm {s} \leq t<10\,\mathrm {s} \\\cos(2\pi 50t/\mathrm {s} )&10\,\mathrm {s} \leq t<15\,\mathrm {s} \\\cos(2\pi 100t/\mathrm {s} )&15\,\mathrm {s} \leq t<20\,\mathrm {s} \\\end{cases}}$

Then it is sampled at 400 Hz. The following spectrograms were produced:

25 ms window	125 ms window
375 ms window	1000 ms window

50 year old Petroleum Engineer Kull from Dawson Creek, spends time with interests such as house brewing, property developers in singapore condo launch and camping. Discovers the beauty in planing a trip to places around the entire world, recently only coming back from .

The 25 ms window allows us to identify a precise time at which the signals change but the precise frequencies are difficult to identify. At the other end of the scale, the 1000 ms window allows the frequencies to be precisely seen but the time between frequency changes is blurred.

Explanation

It can also be explained with reference to the sampling and Nyquist frequency.

Take a window of N samples from an arbitrary real-valued signal at sampling rate f_s . Taking the Fourier transform produces N complex coefficients. Of these coefficients only half are useful (the last N/2 being the complex conjugate of the first N/2 in reverse order, as this is a real valued signal).

These N/2 coefficients represent the frequencies 0 to f_s/2 (Nyquist) and two consecutive coefficients are spaced apart by f_s/N Hz.

To increase the frequency resolution of the window the frequency spacing of the coefficients needs to be reduced. There are only two variables, but decreasing f_s (and keeping N constant) will cause the window size to increase — since there are now fewer samples per unit time. The other alternative is to increase N, but this again causes the window size to increase. So any attempt to increase the frequency resolution causes a larger window size and therefore a reduction in time resolution—and vice-versa.

Application

A STFT being used to analyze an audio signal across time.

STFTs as well as standard Fourier transforms and other tools are frequently used to analyze music. The spectrogram can, for example, show frequency on the horizontal axis, with the lowest frequencies at left, and the highest at the right. The height of each bar (augmented by color) represents the amplitude of the frequencies within that band. The depth dimension represents time, where each new bar was a separate distinct transform. Audio engineers use this kind of visual to gain information about an audio sample, for example, to locate the frequencies of specific noises (especially when used with greater frequency resolution) or to find frequencies which may be more or less resonant in the space where the signal was recorded. This information can be used for equalization or tuning other audio effects.

See also

• Time-frequency representation
• Reassignment method

Other time-frequency transforms:

• wavelet transform
• chirplet transform
• fractional Fourier transform
• Newland transform
• Constant Q transform
• Gabor transform
• S transform

External links

• DiscreteTFDs – software for computing the short-time Fourier transform and other time-frequency distributions
• Singular Spectral Analysis - MultiTaper Method Toolkit - a free software program to analyze short, noisy time series.
• kSpectra Toolkit for Mac OS X from SpectraWorks
• Time stretched short time Fourier transform for time frequency analysis of ultra wideband signals
• A BSD-licensed Matlab class to perform STFT and inverse STFT