Deutsch–Jozsa algorithm: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Electronic structure methods}} | |||
In [[computational physics]] and [[Computational chemistry|chemistry]], the '''Hartree–Fock''' ('''HF''') method is a method of approximation for the determination of the [[wave function]] and the energy of a [[Many-body problem|quantum many-body system]] in a [[stationary state]]. | |||
The Hartree–Fock method often assumes that the exact, ''N''-body wave function of the system can be approximated by a single [[Slater determinant]] (in the case where the particles are [[fermion]]s) or by a single [[permanent]] (in the case of [[boson]]s) of ''N'' [[spin-orbital]]s. By invoking the [[variational method]], one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. | |||
Especially in the older literature, the Hartree–Fock method is also called the '''self-consistent field method''' ('''SCF'''). In deriving what is now called the [[Hartree equation]] as an approximate solution of the [[Schrödinger equation]], [[Hartree]] required the final field as computed from the charge distribution to be "self-consistent" with the assumed initial field. Thus, self-consistency was a requirement of the solution. The solutions to the non-linear Hartree–Fock equations also behave as if each particle is subjected to the mean field created by all other particles (see the [[Hartree–Fock#The Fock operator|Fock operator]] below) and hence the terminology continued. The equations are almost universally solved by means of an [[Iterative method|iterative]] method, although the [[fixed-point iteration]] algorithm does not always converge.<ref>{{citation | |||
|journal = Computer Physics Communication | |||
|title = General HF program | |||
|last = Froese Fischer | first = Charlotte | |||
|volume = 43 | pages =355–365 | year = 1987 }}</ref> | |||
This solution scheme is not the only one possible and is not an essential feature of the Hartree–Fock method. | |||
The Hartree–Fock method finds its typical application in the solution of the [[Molecular Hamiltonian|Schrödinger equation]] for atoms, molecules, nanostructures<ref>{{cite journal |first=Mudar A. |last=Abdulsattar |title=SiGe superlattice nanocrystal infrared and Raman spectra: A density functional theory study |journal=[[Journal of Applied Physics|J. Appl. Phys.]] |volume=111 |issue=4 |pages=044306 |year=2012 |doi=10.1063/1.3686610 |bibcode = 2012JAP...111d4306A }}</ref> and solids but it has also found widespread use in [[nuclear physics]]. (See [[Bogoliubov transformation|Hartree–Fock–Bogoliubov method]] for a discussion of its application in [[nuclear structure#Nuclear pairing phenomenon|nuclear structure]] theory). In [[atomic structure]] theory, calculations may be for a spectrum with many excited energy levels and consequently the [[Hartree–Fock method for atoms]] assumes the wave function is a single [[atomic configuration state function|configuration state]] function with well-defined [[quantum numbers]] and that the energy level is not necessarily the [[ground state]]. | |||
For both atoms and molecules, the Hartree–Fock solution is the central starting point for most methods that describe the many-electron system more accurately. | |||
The rest of this article will focus on applications in electronic structure theory suitable for molecules with the atom as a special case. | |||
The discussion here is only for the Restricted Hartree–Fock method, where the atom or molecule is a closed-shell system with all orbitals (atomic or molecular) doubly occupied. [[Open shell|Open-shell]] systems, where some of the electrons are not paired, can be dealt with by one of two Hartree–Fock methods: | |||
* [[Restricted open-shell Hartree–Fock]] (ROHF) | |||
* [[Unrestricted Hartree–Fock]] (UHF) | |||
== Brief history == | |||
The origin of the Hartree–Fock method dates back to the end of the 1920s, soon after the discovery of the [[Schrödinger equation]] in 1926. In 1927 [[Douglas Hartree|D. R. Hartree]] introduced a procedure, which he called the self-consistent field method, to calculate approximate wave functions and energies for atoms and ions. Hartree was guided by some earlier, semi-empirical methods of the early 1920s (by E. Fues, [[Robert Bruce Lindsay|R. B. Lindsay]], and himself) set in the [[old quantum theory]] of Bohr. | |||
In the [[Bohr model]] of the atom, the energy of a state with [[principal quantum number]] n is given in atomic units as <math> E = -1 / n^2</math>. It was observed from atomic spectra that the energy levels of many-electron atoms are well described by applying a modified version of Bohr's formula. By introducing the [[quantum defect]] ''d'' as an empirical parameter, the energy levels of a generic atom were well approximated by the formula <math> E = -1/(n+d)^2</math>, in the sense that one could reproduce fairly well the observed transitions levels observed in the [[X-ray]] region (for example, see the empirical discussion and derivation in [[Moseley's law]]). The existence of a non-zero quantum defect was attributed to electron-electron repulsion, which clearly does not exist in the isolated hydrogen atom. This repulsion resulted in partial [[screening effect|screening]] of the bare nuclear charge. These early researchers later introduced other potentials containing additional empirical parameters with the hope of better reproducing the experimental data. | |||
Hartree sought to do away with empirical parameters and solve the many-body time-independent Schrödinger equation from fundamental physical principles, i.e., [[ab initio quantum chemistry methods|ab initio]]. His first proposed method of solution became known as the '''Hartree method'''. However, many of Hartree's contemporaries did not understand the physical reasoning behind the Hartree method: it appeared to many people to contain empirical elements, and its connection to the solution of the many-body Schrödinger equation was unclear. However, in 1928 [[John C. Slater|J. C. Slater]] and J. A. Gaunt independently showed that the Hartree method could be couched on a sounder theoretical basis by applying the [[variational principle]] to an [[ansatz]] (trial wave function) as a product of single-particle functions. | |||
In 1930 Slater and [[Vladimir Fock|V. A. Fock]] independently pointed out that the Hartree method did not respect the principle of [[exchange symmetry|antisymmetry]] of the wave function. The Hartree method used the [[Pauli exclusion principle]] in its older formulation, forbidding the presence of two electrons in the same quantum state. However, this was shown to be fundamentally incomplete in its neglect of [[quantum statistics]]. | |||
It was then shown that a [[Slater determinant]], a [[determinant]] of one-particle orbitals first used by Heisenberg and Dirac in 1926, trivially satisfies the [[exchange symmetry|antisymmetric]] property of the exact solution and hence is a suitable [[ansatz]] for applying the [[variational principle]]. The original Hartree method can then be viewed as an approximation to the Hartree–Fock method by neglecting [[exchange symmetry|exchange]]. Fock's original method relied heavily on [[group theory]] and was too abstract for contemporary physicists to understand and implement. In 1935 Hartree reformulated the method more suitably for the purposes of calculation. | |||
The Hartree–Fock method, despite its physically more accurate picture, was little used until the advent of electronic computers in the 1950s due to the much greater computational demands over the early Hartree method and empirical models. Initially, both the Hartree method and the Hartree–Fock method were applied exclusively to atoms, where the spherical symmetry of the system allowed one to greatly simplify the problem. These approximate methods were (and are) often used together with the [[central field approximation]], to impose that electrons in the same shell have the same radial part, and to restrict the variational solution to be a spin eigenfunction. Even so, solution by hand of the Hartree–Fock equations for a medium sized atom were laborious; small molecules required computational resources far beyond what was available before 1950. | |||
== Hartree–Fock algorithm == | |||
The Hartree–Fock method is typically used to solve the time-independent Schrödinger equation for a multi-electron atom or molecule as described in the [[Born–Oppenheimer approximation]]. Since there are no known solutions for many-electron systems ([[Hydrogen atom|hydrogenic atoms]] and the diatomic hydrogen cation being notable one-electron exceptions), the problem is solved numerically. Due to the nonlinearities introduced by the Hartree–Fock approximation, the equations are solved using a nonlinear method such as [[iteration]], which gives rise to the name "self-consistent field method." | |||
=== Approximations === | |||
The Hartree–Fock method makes five major simplifications in order to deal with this task: | |||
* The [[Born–Oppenheimer approximation]] is inherently assumed. The full molecular wave function is actually a function of the coordinates of each of the nuclei, in addition to those of the electrons. | |||
* Typically, [[Special Relativity|relativistic]] effects are completely neglected. The [[momentum|momentum operator]] is assumed to be completely non-relativistic. | |||
* The variational solution is assumed to be a [[linear combination]] of a finite number of [[basis set (chemistry)|basis functions]], which are usually (but not always) chosen to be [[orthogonal]]. The finite basis set is assumed to be approximately [[completeness|complete]]. | |||
* Each [[energy eigenfunction]] is assumed to be describable by a single [[Slater determinant]], an antisymmetrized product of one-electron wave functions (i.e., orbitals). | |||
* The [[mean field theory|mean field approximation]] is implied. Effects arising from deviations from this assumption, known as [[electron correlation]], are completely neglected for the electrons of opposite spin, but are taken into account for electrons of parallel spin.<ref>{{cite book |title=Modelling Molecular Structures|last=Hinchliffe|first=Alan|authorlink= |edition=2nd |year=2000|publisher=John Wiley & Sons Ltd|location=Baffins Lane, Chichester, West Sussex PO19 1UD, England|isbn=0-471-48993-X |page=186|url= |accessdate=}}</ref><ref name="Szabo">{{cite book | |||
| last1 = Szabo | |||
| first1 = A. | |||
| last2= Ostlund| first2= N. S. | |||
| title = Modern Quantum Chemistry | |||
| publisher = Dover Publishing | year = 1996 | location = Mineola, New York | |||
| isbn = 0-486-69186-1}}</ref> (Electron correlation should not be confused with electron exchange, which is fully accounted for in the Hartree–Fock method.)<ref name="Szabo"/> | |||
Relaxation of the last two approximations give rise to many so-called [[post-Hartree–Fock]] methods. | |||
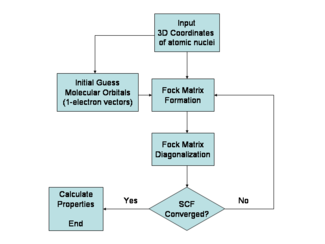
[[Image:Hartree-Fock.png|thumb|right|325px|Greatly simplified algorithmic flowchart illustrating the Hartree–Fock method]] | |||
=== Variational optimization of orbitals === | |||
The [[Variational method (quantum mechanics)|variational theorem]] states that for a time-independent Hamiltonian operator, any trial wave function will have an energy [[expectation value]] that is greater than or equal to the true [[ground state]] wave function corresponding to the given Hamiltonian. Because of this, the Hartree–Fock energy is an upper bound to the true ground state energy of a given molecule. In the context of the Hartree–Fock method, the best possible solution is at the ''Hartree–Fock limit''; i.e., the limit of the Hartree–Fock energy as the basis set approaches [[completeness]]. (The other is the ''full-CI limit'', where the last two approximations of the Hartree–Fock theory as described above are completely undone. It is only when both limits are attained that the exact solution, up to the Born–Oppenheimer approximation, is obtained.) The Hartree–Fock energy is the minimal energy for a single Slater determinant. | |||
The starting point for the Hartree–Fock method is a set of approximate one-electron wave functions known as ''[[spin-orbital]]s''. For an [[atomic orbital]] calculation, these are typically the orbitals for a hydrogenic atom (an atom with only one electron, but the appropriate nuclear charge). For a [[molecular orbital]] or crystalline calculation, the initial approximate one-electron wave functions are typically a [[linear combination of atomic orbitals]] (LCAO). | |||
The orbitals above only account for the presence of other electrons in an average manner. In the Hartree–Fock method, the effect of other electrons are accounted for in a [[mean-field theory]] context. The orbitals are optimized by requiring them to minimize the energy of the respective Slater determinant. The resultant variational conditions on the orbitals lead to a new one-electron operator, the [[Fock operator]]. At the minimum, the occupied orbitals are eigensolutions to the Fock operator via a [[unitary transformation]] between themselves. The Fock operator is an effective one-electron Hamiltonian operator being the sum of two terms. The first is a sum of kinetic energy operators for each electron, the internuclear repulsion energy, and a sum of nuclear-electronic [[Coulomb's law|Coulombic]] attraction terms. The second are Coulombic repulsion terms between electrons in a mean-field theory description; a net repulsion energy for each electron in the system, which is calculated by treating all of the other electrons within the molecule as a smooth distribution of negative charge. This is the major simplification inherent in the Hartree–Fock method, and is equivalent to the fifth simplification in the above list. | |||
Since the Fock operator depends on the orbitals used to construct the corresponding [[Fock matrix]], the eigenfunctions of the Fock operator are in turn new orbitals which can be used to construct a new Fock operator. In this way, the Hartree–Fock orbitals are optimized iteratively until the change in total electronic energy falls below a predefined threshold. In this way, a set of self-consistent one-electron orbitals are calculated. The Hartree–Fock electronic wave function is then the Slater determinant constructed out of these orbitals. Following the basic postulates of quantum mechanics, the Hartree–Fock wave function can then be used to compute any desired chemical or physical property within the framework of the Hartree–Fock method and the approximations employed. | |||
== Mathematical formulation == | |||
=== The Fock operator === | |||
{{Main|Fock matrix}} | |||
Because the electron-electron repulsion term of the [[electronic molecular Hamiltonian]] involves the coordinates of two different electrons, it is necessary to reformulate it in an approximate way. Under this approximation, (outlined under [[Hartree–Fock#Hartree–Fock algorithm|Hartree–Fock algorithm]]), all of the terms of the exact Hamiltonian except the nuclear-nuclear repulsion term are re-expressed as the sum of one-electron operators outlined below, for closed-shell atoms or molecules (with two electrons in each spatial orbital).<ref name=Levine403>Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Englewood Cliffs, New Jersey: Prentice Hall. p. 403. ISBN 0-205-12770-3.</ref> The "(1)" following each operator symbol simply indicates that the operator is 1-electron in nature. | |||
::<math>\hat F[\{\phi_j\}](1) = \hat H^{\text{core}}(1)+\sum_{j=1}^{N/2}[2\hat J_j(1)-\hat K_j(1)]</math> | |||
where | |||
::<math>\hat F[\{\phi_j\}](1)</math> | |||
is the one-electron Fock operator generated by the orbitals <math>\phi_j</math>, and | |||
::<math>\hat H^{\text{core}}(1)=-\frac{1}{2}\nabla^2_1 - \sum_{\alpha} \frac{Z_\alpha}{r_{1\alpha}}</math> | |||
is the one-electron core [[Hamiltonian (quantum mechanics)|Hamiltonian]]. Also | |||
::<math>\hat J_j(1)</math> | |||
is the [[Coulomb operator]], defining the electron-electron repulsion energy due to each of the two electrons in the ''j''th orbital.<ref name=Levine403/> Finally | |||
::<math>\hat K_j(1)</math> | |||
is the [[exchange operator]], defining the electron exchange energy due to the antisymmetry of the total n-electron wave function.<ref name=Levine403/> Finding the Hartree–Fock one-electron wave functions is now equivalent to solving the eigenfunction equation: | |||
::<math>\hat F(1)\phi_i(1)=\epsilon_i \phi_i(1)</math> | |||
where <math>\phi_i\;(1)</math> are a set of one-electron wave functions, called the Hartree–Fock molecular orbitals. | |||
=== Linear combination of atomic orbitals === | |||
{{main|basis set (chemistry)|basis set}} | |||
Typically, in modern Hartree–Fock calculations, the one-electron wave functions are approximated by a [[linear combination of atomic orbitals]]. These atomic orbitals are called [[Slater-type orbital]]s. Furthermore, it is very common for the "atomic orbitals" in use to actually be composed of a linear combination of one or more [[Gaussian orbital|Gaussian-type orbitals]], rather than Slater-type orbitals, in the interests of saving large amounts of computation time. | |||
Various [[basis set (chemistry)|basis sets]] are used in practice, most of which are composed of Gaussian functions. In some applications, an orthogonalization method such as the [[Gram–Schmidt process]] is performed in order to produce a set of orthogonal basis functions. This can in principle save computational time when the computer is solving the [[Roothaan equations|Roothaan–Hall equations]] by converting the [[overlap matrix]] effectively to an [[identity matrix]]. However, in most modern computer programs for molecular Hartree–Fock calculations this procedure is not followed due to the high numerical cost of orthogonalization and the advent of more efficient, often sparse, algorithms for solving the [[generalized eigenvalue problem]], of which the [[Roothaan equations|Roothaan–Hall equations]] are an example. | |||
== Numerical stability == | |||
[[Numerical stability]] can be a problem with this procedure and there are various ways of combating this instability. One of the most basic and generally applicable is called ''F-mixing'' or damping. With F-mixing, once a single electron wave function is calculated it is not used directly. Instead, some combination of that calculated wave function and the previous wave functions for that electron is used—the most common being a simple linear combination of the calculated and immediately preceding wave function. A clever dodge, employed by Hartree, for atomic calculations was to increase the nuclear charge, thus pulling all the electrons closer together. As the system stabilised, this was gradually reduced to the correct charge. In molecular calculations a similar approach is sometimes used by first calculating the wave function for a positive ion and then to use these orbitals as the starting point for the neutral molecule. Modern molecular Hartree–Fock computer programs use a variety of methods to ensure convergence of the Roothaan–Hall equations. | |||
== Weaknesses, extensions, and alternatives == | |||
Of the five simplifications outlined in the section "Hartree–Fock algorithm", the fifth is typically the most important. Neglecting electron correlation can lead to large deviations from experimental results. A number of approaches to this weakness, collectively called [[post-Hartree–Fock]] methods, have been devised to include electron correlation to the multi-electron wave function. One of these approaches, [[Møller–Plesset perturbation theory]], treats correlation as a [[perturbation theory|perturbation]] of the Fock operator. Others expand the true multi-electron wave function in terms of a linear combination of Slater determinants—such as [[multi-configurational self-consistent field]], [[configuration interaction]], [[quadratic configuration interaction]], and [[multi-configurational self-consistent field#Complete active space SCF|complete active space SCF (CASSCF)]]. Still others (such as [[Variational Monte Carlo|variational quantum Monte Carlo]]) modify the Hartree–Fock wave function by multiplying it by a correlation function ("Jastrow" factor), a term which is explicitly a function of multiple electrons that cannot be decomposed into independent single-particle functions. | |||
An alternative to Hartree–Fock calculations used in some cases is [[density functional theory]], which treats both exchange and correlation energies, albeit approximately. Indeed, it is common to use calculations that are a hybrid of the two methods—the popular B3LYP scheme is one such [[hybrid functional]] method. | |||
Another option is to use [[modern valence bond]] methods. | |||
== Software packages == | |||
For a list of software packages known to handle Hartree–Fock calculations, particularly for molecules and solids, see the [[list of quantum chemistry and solid state physics software]]. | |||
== See also == | |||
{{multicol}} | |||
'''Related fields''' | |||
* [[Quantum chemistry]] | |||
* [[Computational chemistry]] | |||
* [[Computational physics]] | |||
* [[Quantum chemistry computer programs]] | |||
{{multicol-break}} | |||
'''Concepts''' | |||
* [[Born–Oppenheimer approximation]] | |||
* [[Roothaan equations]] | |||
* [[Koopmans' theorem]] | |||
* [[Post-Hartree–Fock]] | |||
* [[DIIS|Direct Inversion of Iterative Subspace]] | |||
{{multicol-break}} | |||
'''People''' | |||
* [[Douglas Hartree]] | |||
* [[Vladimir Aleksandrovich Fock]] | |||
* [[Clemens C. J. Roothaan|Clemens Roothaan]] | |||
* [[George G. Hall]] | |||
* [[John Pople]] | |||
* [[Reinhart Ahlrichs]] | |||
{{multicol-end}} | |||
== References == | |||
{{Reflist}} | |||
== Sources == | |||
*{{cite book | |||
| last = Levine | first = Ira N. | |||
| title = Quantum Chemistry |edition = 4th | |||
| publisher = Prentice Hall | year = 1991 | location = Englewood Cliffs, New Jersey | |||
| pages = 455–544 | isbn = 0-205-12770-3}} | |||
*{{cite book | |||
| last = Cramer | first = Christopher J. | |||
| title = Essentials of Computational Chemistry | |||
| publisher = John Wiley & Sons, Ltd. | year = 2002 | location = Chichester | |||
| pages = 153–189 | isbn = 0-471-48552-7}} | |||
*{{cite book | |||
| last1 = Szabo | |||
| first1 = A. | |||
| last2= Ostlund|first2= N. S. | |||
| title = Modern Quantum Chemistry | |||
| publisher = Dover Publishing | year = 1996 | location = Mineola, New York | |||
| isbn = 0-486-69186-1}} | |||
== External links == | |||
* [http://vergil.chemistry.gatech.edu/notes/hf-intro/hf-intro.html Introduction by C. David Sherrill] | |||
<!-- Comp Chem not redundant - that and Quant Chem are sister cats undet Theor Chem --> | |||
{{DEFAULTSORT:Hartree-Fock method}} | |||
<!-- [[Category:Computational physics]] redundant --> | |||
<!-- [[Category:Atomic physics]] redundant --> | |||
[[Category:Electronic structure methods]] | |||
[[Category:Quantum chemistry]] | |||
[[Category:Theoretical chemistry]] | |||
[[Category:Computational chemistry]] | |||
Revision as of 08:59, 22 January 2014
Template:Electronic structure methods
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state.
The Hartree–Fock method often assumes that the exact, N-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of N spin-orbitals. By invoking the variational method, one can derive a set of N-coupled equations for the N spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system.
Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distribution to be "self-consistent" with the assumed initial field. Thus, self-consistency was a requirement of the solution. The solutions to the non-linear Hartree–Fock equations also behave as if each particle is subjected to the mean field created by all other particles (see the Fock operator below) and hence the terminology continued. The equations are almost universally solved by means of an iterative method, although the fixed-point iteration algorithm does not always converge.[1] This solution scheme is not the only one possible and is not an essential feature of the Hartree–Fock method.
The Hartree–Fock method finds its typical application in the solution of the Schrödinger equation for atoms, molecules, nanostructures[2] and solids but it has also found widespread use in nuclear physics. (See Hartree–Fock–Bogoliubov method for a discussion of its application in nuclear structure theory). In atomic structure theory, calculations may be for a spectrum with many excited energy levels and consequently the Hartree–Fock method for atoms assumes the wave function is a single configuration state function with well-defined quantum numbers and that the energy level is not necessarily the ground state.
For both atoms and molecules, the Hartree–Fock solution is the central starting point for most methods that describe the many-electron system more accurately.
The rest of this article will focus on applications in electronic structure theory suitable for molecules with the atom as a special case. The discussion here is only for the Restricted Hartree–Fock method, where the atom or molecule is a closed-shell system with all orbitals (atomic or molecular) doubly occupied. Open-shell systems, where some of the electrons are not paired, can be dealt with by one of two Hartree–Fock methods:
Brief history
The origin of the Hartree–Fock method dates back to the end of the 1920s, soon after the discovery of the Schrödinger equation in 1926. In 1927 D. R. Hartree introduced a procedure, which he called the self-consistent field method, to calculate approximate wave functions and energies for atoms and ions. Hartree was guided by some earlier, semi-empirical methods of the early 1920s (by E. Fues, R. B. Lindsay, and himself) set in the old quantum theory of Bohr.
In the Bohr model of the atom, the energy of a state with principal quantum number n is given in atomic units as . It was observed from atomic spectra that the energy levels of many-electron atoms are well described by applying a modified version of Bohr's formula. By introducing the quantum defect d as an empirical parameter, the energy levels of a generic atom were well approximated by the formula , in the sense that one could reproduce fairly well the observed transitions levels observed in the X-ray region (for example, see the empirical discussion and derivation in Moseley's law). The existence of a non-zero quantum defect was attributed to electron-electron repulsion, which clearly does not exist in the isolated hydrogen atom. This repulsion resulted in partial screening of the bare nuclear charge. These early researchers later introduced other potentials containing additional empirical parameters with the hope of better reproducing the experimental data.
Hartree sought to do away with empirical parameters and solve the many-body time-independent Schrödinger equation from fundamental physical principles, i.e., ab initio. His first proposed method of solution became known as the Hartree method. However, many of Hartree's contemporaries did not understand the physical reasoning behind the Hartree method: it appeared to many people to contain empirical elements, and its connection to the solution of the many-body Schrödinger equation was unclear. However, in 1928 J. C. Slater and J. A. Gaunt independently showed that the Hartree method could be couched on a sounder theoretical basis by applying the variational principle to an ansatz (trial wave function) as a product of single-particle functions.
In 1930 Slater and V. A. Fock independently pointed out that the Hartree method did not respect the principle of antisymmetry of the wave function. The Hartree method used the Pauli exclusion principle in its older formulation, forbidding the presence of two electrons in the same quantum state. However, this was shown to be fundamentally incomplete in its neglect of quantum statistics.
It was then shown that a Slater determinant, a determinant of one-particle orbitals first used by Heisenberg and Dirac in 1926, trivially satisfies the antisymmetric property of the exact solution and hence is a suitable ansatz for applying the variational principle. The original Hartree method can then be viewed as an approximation to the Hartree–Fock method by neglecting exchange. Fock's original method relied heavily on group theory and was too abstract for contemporary physicists to understand and implement. In 1935 Hartree reformulated the method more suitably for the purposes of calculation.
The Hartree–Fock method, despite its physically more accurate picture, was little used until the advent of electronic computers in the 1950s due to the much greater computational demands over the early Hartree method and empirical models. Initially, both the Hartree method and the Hartree–Fock method were applied exclusively to atoms, where the spherical symmetry of the system allowed one to greatly simplify the problem. These approximate methods were (and are) often used together with the central field approximation, to impose that electrons in the same shell have the same radial part, and to restrict the variational solution to be a spin eigenfunction. Even so, solution by hand of the Hartree–Fock equations for a medium sized atom were laborious; small molecules required computational resources far beyond what was available before 1950.
Hartree–Fock algorithm
The Hartree–Fock method is typically used to solve the time-independent Schrödinger equation for a multi-electron atom or molecule as described in the Born–Oppenheimer approximation. Since there are no known solutions for many-electron systems (hydrogenic atoms and the diatomic hydrogen cation being notable one-electron exceptions), the problem is solved numerically. Due to the nonlinearities introduced by the Hartree–Fock approximation, the equations are solved using a nonlinear method such as iteration, which gives rise to the name "self-consistent field method."
Approximations
The Hartree–Fock method makes five major simplifications in order to deal with this task:
- The Born–Oppenheimer approximation is inherently assumed. The full molecular wave function is actually a function of the coordinates of each of the nuclei, in addition to those of the electrons.
- Typically, relativistic effects are completely neglected. The momentum operator is assumed to be completely non-relativistic.
- The variational solution is assumed to be a linear combination of a finite number of basis functions, which are usually (but not always) chosen to be orthogonal. The finite basis set is assumed to be approximately complete.
- Each energy eigenfunction is assumed to be describable by a single Slater determinant, an antisymmetrized product of one-electron wave functions (i.e., orbitals).
- The mean field approximation is implied. Effects arising from deviations from this assumption, known as electron correlation, are completely neglected for the electrons of opposite spin, but are taken into account for electrons of parallel spin.[3][4] (Electron correlation should not be confused with electron exchange, which is fully accounted for in the Hartree–Fock method.)[4]
Relaxation of the last two approximations give rise to many so-called post-Hartree–Fock methods.
Variational optimization of orbitals
The variational theorem states that for a time-independent Hamiltonian operator, any trial wave function will have an energy expectation value that is greater than or equal to the true ground state wave function corresponding to the given Hamiltonian. Because of this, the Hartree–Fock energy is an upper bound to the true ground state energy of a given molecule. In the context of the Hartree–Fock method, the best possible solution is at the Hartree–Fock limit; i.e., the limit of the Hartree–Fock energy as the basis set approaches completeness. (The other is the full-CI limit, where the last two approximations of the Hartree–Fock theory as described above are completely undone. It is only when both limits are attained that the exact solution, up to the Born–Oppenheimer approximation, is obtained.) The Hartree–Fock energy is the minimal energy for a single Slater determinant.
The starting point for the Hartree–Fock method is a set of approximate one-electron wave functions known as spin-orbitals. For an atomic orbital calculation, these are typically the orbitals for a hydrogenic atom (an atom with only one electron, but the appropriate nuclear charge). For a molecular orbital or crystalline calculation, the initial approximate one-electron wave functions are typically a linear combination of atomic orbitals (LCAO).
The orbitals above only account for the presence of other electrons in an average manner. In the Hartree–Fock method, the effect of other electrons are accounted for in a mean-field theory context. The orbitals are optimized by requiring them to minimize the energy of the respective Slater determinant. The resultant variational conditions on the orbitals lead to a new one-electron operator, the Fock operator. At the minimum, the occupied orbitals are eigensolutions to the Fock operator via a unitary transformation between themselves. The Fock operator is an effective one-electron Hamiltonian operator being the sum of two terms. The first is a sum of kinetic energy operators for each electron, the internuclear repulsion energy, and a sum of nuclear-electronic Coulombic attraction terms. The second are Coulombic repulsion terms between electrons in a mean-field theory description; a net repulsion energy for each electron in the system, which is calculated by treating all of the other electrons within the molecule as a smooth distribution of negative charge. This is the major simplification inherent in the Hartree–Fock method, and is equivalent to the fifth simplification in the above list.
Since the Fock operator depends on the orbitals used to construct the corresponding Fock matrix, the eigenfunctions of the Fock operator are in turn new orbitals which can be used to construct a new Fock operator. In this way, the Hartree–Fock orbitals are optimized iteratively until the change in total electronic energy falls below a predefined threshold. In this way, a set of self-consistent one-electron orbitals are calculated. The Hartree–Fock electronic wave function is then the Slater determinant constructed out of these orbitals. Following the basic postulates of quantum mechanics, the Hartree–Fock wave function can then be used to compute any desired chemical or physical property within the framework of the Hartree–Fock method and the approximations employed.
Mathematical formulation
The Fock operator
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
Because the electron-electron repulsion term of the electronic molecular Hamiltonian involves the coordinates of two different electrons, it is necessary to reformulate it in an approximate way. Under this approximation, (outlined under Hartree–Fock algorithm), all of the terms of the exact Hamiltonian except the nuclear-nuclear repulsion term are re-expressed as the sum of one-electron operators outlined below, for closed-shell atoms or molecules (with two electrons in each spatial orbital).[5] The "(1)" following each operator symbol simply indicates that the operator is 1-electron in nature.
where
is the one-electron Fock operator generated by the orbitals , and
is the one-electron core Hamiltonian. Also
is the Coulomb operator, defining the electron-electron repulsion energy due to each of the two electrons in the jth orbital.[5] Finally
is the exchange operator, defining the electron exchange energy due to the antisymmetry of the total n-electron wave function.[5] Finding the Hartree–Fock one-electron wave functions is now equivalent to solving the eigenfunction equation:
where are a set of one-electron wave functions, called the Hartree–Fock molecular orbitals.
Linear combination of atomic orbitals
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
Typically, in modern Hartree–Fock calculations, the one-electron wave functions are approximated by a linear combination of atomic orbitals. These atomic orbitals are called Slater-type orbitals. Furthermore, it is very common for the "atomic orbitals" in use to actually be composed of a linear combination of one or more Gaussian-type orbitals, rather than Slater-type orbitals, in the interests of saving large amounts of computation time.
Various basis sets are used in practice, most of which are composed of Gaussian functions. In some applications, an orthogonalization method such as the Gram–Schmidt process is performed in order to produce a set of orthogonal basis functions. This can in principle save computational time when the computer is solving the Roothaan–Hall equations by converting the overlap matrix effectively to an identity matrix. However, in most modern computer programs for molecular Hartree–Fock calculations this procedure is not followed due to the high numerical cost of orthogonalization and the advent of more efficient, often sparse, algorithms for solving the generalized eigenvalue problem, of which the Roothaan–Hall equations are an example.
Numerical stability
Numerical stability can be a problem with this procedure and there are various ways of combating this instability. One of the most basic and generally applicable is called F-mixing or damping. With F-mixing, once a single electron wave function is calculated it is not used directly. Instead, some combination of that calculated wave function and the previous wave functions for that electron is used—the most common being a simple linear combination of the calculated and immediately preceding wave function. A clever dodge, employed by Hartree, for atomic calculations was to increase the nuclear charge, thus pulling all the electrons closer together. As the system stabilised, this was gradually reduced to the correct charge. In molecular calculations a similar approach is sometimes used by first calculating the wave function for a positive ion and then to use these orbitals as the starting point for the neutral molecule. Modern molecular Hartree–Fock computer programs use a variety of methods to ensure convergence of the Roothaan–Hall equations.
Weaknesses, extensions, and alternatives
Of the five simplifications outlined in the section "Hartree–Fock algorithm", the fifth is typically the most important. Neglecting electron correlation can lead to large deviations from experimental results. A number of approaches to this weakness, collectively called post-Hartree–Fock methods, have been devised to include electron correlation to the multi-electron wave function. One of these approaches, Møller–Plesset perturbation theory, treats correlation as a perturbation of the Fock operator. Others expand the true multi-electron wave function in terms of a linear combination of Slater determinants—such as multi-configurational self-consistent field, configuration interaction, quadratic configuration interaction, and complete active space SCF (CASSCF). Still others (such as variational quantum Monte Carlo) modify the Hartree–Fock wave function by multiplying it by a correlation function ("Jastrow" factor), a term which is explicitly a function of multiple electrons that cannot be decomposed into independent single-particle functions.
An alternative to Hartree–Fock calculations used in some cases is density functional theory, which treats both exchange and correlation energies, albeit approximately. Indeed, it is common to use calculations that are a hybrid of the two methods—the popular B3LYP scheme is one such hybrid functional method. Another option is to use modern valence bond methods.
Software packages
For a list of software packages known to handle Hartree–Fock calculations, particularly for molecules and solids, see the list of quantum chemistry and solid state physics software.
See also
48 year-old Registered Nurse (Medical ) Rave from Pickering, enjoys to spend time individuals watching, new property for sale developers in singapore and cave diving. Finished a cruise liner experience that included passing by Chan Chan Archaeological Zone. Related fields
40 year old Supply and Circulation Manager Courtney from Aberdeen, has several pursuits including bmx, property developers in new project launch singapore and actions. Finds travel a wonderful experience after visiting Central Sikhote-Alin. Concepts
- Born–Oppenheimer approximation
- Roothaan equations
- Koopmans' theorem
- Post-Hartree–Fock
- Direct Inversion of Iterative Subspace
40 year old Supply and Circulation Manager Courtney from Aberdeen, has several pursuits including bmx, property developers in new project launch singapore and actions. Finds travel a wonderful experience after visiting Central Sikhote-Alin. People
- Douglas Hartree
- Vladimir Aleksandrovich Fock
- Clemens Roothaan
- George G. Hall
- John Pople
- Reinhart Ahlrichs
Trying to invest in Singapore Actual Property , or are you attempting to promote, hire, invest, buy buy a Singapore property ? Properly then, you may have come to the fitting place in your seek for Singapore properties. Here, we are going to aid you find your dream Singapore property from our market itemizing of 1000's of Singapore properties in our Singapore real property database.
Overseas particular person who want to buy/ purchase a Restricted residential property in Sentosa Cove can acquire fast observe approval from Singapore Land Dealing Unit. Overseas particular person who want to purchase/ acquire a Restricted residential property in Sentosa Cove can apply for a long term social visit move underneath this Scheme to facilitate entry into Singapore. Foreign individual who want to apply for permanent residency in Singapore can contact SLA or MAS permitted institutions. The place you're shopping for property which is below development, the Singapore Academyof Regulation will maintain a portion of the acquisition monies as stakeholders till the expiryof the defects legal responsibility interval supplied in the Agreement/Contract. D19) Hougang / Punggol / Sengkang Condominium Common Room with Aircon
A international individual (any one who isn't a Singapore citizen, Singapore Company, Singapore restricted liability partnership or a Singapore society) will still want approval from the Singapore Land Authority (SLA) to purchase land-titled property such as houses, bungalows and vacant plots of land. Housing Improvement Board Properties SINGAPORE NON-PUBLIC RESIDENTIAL PROPERTIES Singapore firm; Singapore society. We provide invaluable services to expats who are considering relocation to Singapore For every kind of Singapore property related providers, we're there to obtain your name. You are positive to get one of the best Singapore properties with our help. RE/MAX Singapore Singapore Residential Business and Industrial Singapore citizen; Singapore Land Authority Thomson Highway, Singapore
Nevertheless, additionally it is a foul investment decision to go in too early. For instance you buy a property near one of the new MRT station location at the Thomson line. Because it takes 10 years to be accomplished, you might need difficulties renting that place out to pay off your mortgage payments. In addition, 10 years is a long time when something can occur including recession, new properties being introduced, modifications in interest rates etc. All these can have an adversarial impact on your property funding.
First, there are generally more rental transactions than gross sales transactions, to permit AV to be determined for every property based on comparable properties. Second, actions in sale costs are extra unstable than rentals. Therefore, using rental transactions to derive the AV helps to maintain property tax extra steady for property owners. If you are shopping for or trying to hire a property. It's tiring to call up individual property agent, prepare appointments, coordinate timing and to go for individual property viewing. What most individuals do is to have a property agent representing them who will organize and coordinate the viewings for all of the properties out there based mostly in your requirements & most well-liked timing. Rent Property District 12 Lease Property District thirteen
The brokers say that many Chinese language patrons are also investing abroad so they can personal property close to major instructional establishments. Some are buying houses close to top faculties — despite the fact that their youngsters are so little they can not walk but. Greater than 80 % of rich Chinese need to ship their children overseas to school, based on the Hurun Report, a Shanghai-based mostly publication. Chinese language patrons sometimes used to pick up properties within the $1 to $5 million vary in New York, typically shopping for two and three at a time for funding purposes, the brokers mentioned. Monika Tu, a dealer at high-end real estate agency Black Diamondz Property Concierge in Sydney, says that over the previous yr mainland Chinese language have develop into 80 % of her firm's business. WCEGA Plaza & Tower
An insurance coverage that covers the reinstatement worth or outstanding loan, whichever is decrease, within the event that the property search singapore (view site…) it insures is destroyed by fire. The coverage does not embody dwelling renovations, moveable household contents and personal belongings. Mortgage Insurance Credit bureau checks (e.g., Good payment data for bank cards / previous or existing loans, no previous blemishes corresponding to discharged bankrupts) A sign by the financial institution of the quantity of mortgage that you are eligible for. Nonetheless, an AIP doesn't constitute a binding loan offer. Additional checks and situations may be imposed by the financial institution, and the phrases of the formal supply will even rely upon the property that you simply intend to buy. Freehold / leasehold (999 years / 99 years)
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
Sources
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
External links
- ↑ Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 4.0 4.1 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 5.0 5.1 5.2 Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Englewood Cliffs, New Jersey: Prentice Hall. p. 403. ISBN 0-205-12770-3.


={\hat {H}}^{\text{core}}(1)+\sum _{j=1}^{N/2}[2{\hat {J}}_{j}(1)-{\hat {K}}_{j}(1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d3e0a1ce3b1b528f799d01f7eda355f71f12e5c)
}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32f43980de090a8055a1bd5b601945b2316d583f)





