Pisano period: Difference between revisions
en>Bibcode Bot m Adding 1 arxiv eprint(s), 0 bibcode(s) and 0 doi(s). Did it miss something? Report bugs, errors, and suggestions at User talk:Bibcode Bot |
en>JMOprof →External links: added youtube video about pisano periods by Dr James Grime and the University of Nottingham |
||
| Line 1: | Line 1: | ||
{{Infobox polyhedron | |||
|image=Pentagonal pyramid.png | |||
|type=[[Johnson solid|Johnson]]<br>[[square pyramid|J<sub>1</sub>]] - '''J<sub>2</sub>''' - [[triangular cupola|J<sub>3</sub>]] | |||
|faces=5 [[triangle]]s<br>1 [[pentagon]] | |||
|edges=10 | |||
|vertices=6 | |||
|symmetry=''C''<sub>5v</sub>, [5], (*55) | |||
|rotation_group=''C''<sub>5</sub>, [5]<sup>+</sup>, (55) | |||
|vertex_config=5(3<sup>2</sup>.5)<br>(3<sup>5</sup>) | |||
|dual=self | |||
|properties=[[convex set|convex]] | |||
|net=pentagonal pyramid flat.svg | |||
}} | |||
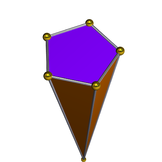
In [[geometry]], a '''pentagonal pyramid''' is a [[Pyramid (geometry)| pyramid]] with a [[pentagon]]al base upon which are erected five [[triangle|triangular]] faces that meet at a point (the vertex). Like any [[pyramid]], it is self-[[dual polyhedron|dual]]. | |||
The ''regular'' pentagonal pyramid has a base that is a regular pentagon and lateral faces that are [[equilateral triangle]]s. It is one of the [[Johnson solid]]s (''J''<sub>2</sub>). Its height ''H'', from the midpoint of the pentagonal face to the apex, (as a function of ''a'', where ''a'' is the side length), can be computed as: | |||
:<math>H = \sqrt{{\frac{5-\sqrt{5}}{10}}}\,a \approx 0.5257\,a.</math><!--unchecked--> | |||
Its surface area, ''A'', can be computed as the area of pentagonal base plus five times the area of one triangle: | |||
:<math>A = \left( \frac{\sqrt{25 + 10 \sqrt{5}}}{4} + 5\frac{\sqrt{3}}{4} \right) a^2 \approx 3.8855\,a^2.</math><!--checked--> | |||
Its volume when an edge length is known can be figured out with this formula: | |||
:<math>V = \frac{5 + \sqrt{5}}{24}\,a^3 \approx 0.3015\,a^3.</math><!--unchecked--> | |||
It can be seen as the "lid" of an [[icosahedron]]; the rest of the icosahedron forms a [[gyroelongated pentagonal pyramid]], ''J''<sub>11</sub>, one of the 92 Johnson solids named and described by [[Norman Johnson (mathematician)|Norman Johnson]] in 1966. | |||
More generally an order-2 vertex-uniform pentagonal pyramid can be defined with a regular pentagonal base and 5 isosceles triangle sides of any height. | |||
== Related polyhedra == | |||
{{Pyramids}} | |||
{| class=wikitable width=320 | |||
|[[File:Pentagonal frustum.svg|160px]]<br>Pentagonal [[frustum]] is a pentagonal pyramid with its apex truncated | |||
|[[File:Icosahedron.png|160px]]<br>The vertex of an [[icosahedron]] is a pentagonal pyramid | |||
|} | |||
=== Dual polyhedron === | |||
The pentagonal pyramid is topologically a [[self-dual polyhedron]]. The dual edge lengths are different due to the [[polar reciprocation]]. | |||
{| class=wikitable width=320 | |||
|- valign=top | |||
!Dual pentagonal pyramid | |||
!Net of dual | |||
|- valign=top | |||
|[[File:Dual pentagonal pyramid.png|162px]] | |||
|[[File:Dual pentagonal pyramid net.png|160px]] | |||
|} | |||
==External links== | |||
* {{Mathworld2 | urlname2 = JohnsonSolid | title2 = Johnson solid | urlname = PentagonalPyramid | title = Pentagonal pyramid}} | |||
*[http://www.georgehart.com/virtual-polyhedra/vp.html Virtual Reality Polyhedra] www.georgehart.com: The Encyclopedia of Polyhedra ( [[VRML]] [http://www.georgehart.com/virtual-polyhedra/vrml/pentagonal_pyramid_(J2).wrl model]) | |||
[[Category:Pyramids and bipyramids]] | |||
[[Category:Self-dual polyhedra]] | |||
[[Category:Prismatoid polyhedra]] | |||
[[Category:Johnson solids]] | |||
{{Polyhedron navigator}} | |||
Revision as of 17:49, 19 October 2013
Chiropractor Rave from Barrie, loves to spend some time fast, property market singapore developers in singapore and warhammer. Finds inspiration by going to Cistercian Abbey of Fontenay. In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point (the vertex). Like any pyramid, it is self-dual.
The regular pentagonal pyramid has a base that is a regular pentagon and lateral faces that are equilateral triangles. It is one of the Johnson solids (J2). Its height H, from the midpoint of the pentagonal face to the apex, (as a function of a, where a is the side length), can be computed as:
Its surface area, A, can be computed as the area of pentagonal base plus five times the area of one triangle:
Its volume when an edge length is known can be figured out with this formula:
It can be seen as the "lid" of an icosahedron; the rest of the icosahedron forms a gyroelongated pentagonal pyramid, J11, one of the 92 Johnson solids named and described by Norman Johnson in 1966.
More generally an order-2 vertex-uniform pentagonal pyramid can be defined with a regular pentagonal base and 5 isosceles triangle sides of any height.
Related polyhedra
 Pentagonal frustum is a pentagonal pyramid with its apex truncated |
 The vertex of an icosahedron is a pentagonal pyramid |
Dual polyhedron
The pentagonal pyramid is topologically a self-dual polyhedron. The dual edge lengths are different due to the polar reciprocation.
| Dual pentagonal pyramid | Net of dual |
|---|---|
|

|
External links
- Template:Mathworld2
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra ( VRML model)


