Hopf conjecture: Difference between revisions
en>Giftlite |
en>EmausBot m Bot: Migrating 1 interwiki links, now provided by Wikidata on d:Q5900498 |
||
| Line 1: | Line 1: | ||
[[File:Parabolic cylindrical coordinates.png|thumb|right|350px|[[Coordinate system#Coordinate surface|Coordinate surfaces]] of parabolic cylindrical coordinates. The red parabolic cylinder corresponds to σ=2, whereas the yellow parabolic cylinder corresponds to τ=1. The blue plane corresponds to ''z''=2. These surfaces intersect at the point '''P''' (shown as a black sphere), which has [[Cartesian coordinate system|Cartesian coordinates]] roughly (2, -1.5, 2).]] | |||
In [[mathematics]], '''parabolic cylindrical coordinates''' are a three-dimensional [[orthogonal coordinates|orthogonal]] [[coordinate system]] that results from projecting the two-dimensional [[parabolic coordinates|parabolic coordinate system]] in the | |||
perpendicular <math>z</math>-direction. Hence, the [[Coordinate system#Coordinate surface|coordinate surfaces]] are [[confocal]] [[parabola|parabolic]] cylinders. Parabolic cylindrical coordinates have found many applications, e.g., the [[potential theory]] of edges. | |||
==Basic definition== | |||
[[File:Parabolic coords.svg|thumb|right|250px|Parabolic coordinate system showing curves of constant σ and τ the horizontal and vertical axes are the x and y coordinates respectively. These coordinates are projected along the z-axis, and so this diagram will hold for any value of the z coordinate.]] | |||
The parabolic cylindrical coordinates <math>(\sigma, \tau, z)</math> are defined in terms of the [[Cartesian coordinates]] ''(x,y,z)'' by: | |||
:<math>x = \sigma \tau\,</math> | |||
:<math>y = \frac{1}{2} \left( \tau^{2} - \sigma^{2} \right)</math> | |||
:<math>z = z\,</math> | |||
The surfaces of constant <math>\sigma</math> form confocal parabolic cylinders | |||
:<math> | |||
2y = \frac{x^{2}}{\sigma^{2}} - \sigma^{2} | |||
</math> | |||
that open towards <math>+y</math>, whereas the surfaces of constant <math>\tau</math> form confocal parabolic cylinders | |||
:<math> | |||
2y = -\frac{x^{2}}{\tau^{2}} + \tau^{2} | |||
</math> | |||
that open in the opposite direction, i.e., towards <math>-y</math>. The foci of all these parabolic cylinders are located along the line defined by <math>x=y=0</math>. The radius ''r'' has a simple formula as well | |||
:<math> | |||
r = \sqrt{x^{2} + y^{2}} = \frac{1}{2} \left( \sigma^{2} + \tau^{2} \right) | |||
</math> | |||
that proves useful in solving the [[Hamilton-Jacobi equation]] in parabolic coordinates for the [[inverse-square law|inverse-square]] [[central force]] problem of [[mechanics]]; for further details, see the [[Laplace–Runge–Lenz vector]] article. | |||
==Scale factors== | |||
The scale factors for the parabolic cylindrical coordinates <math>\sigma</math> and <math>\tau</math> are: | |||
:<math> | |||
h_{\sigma} = h_{\tau} = \sqrt{\sigma^{2} + \tau^{2}} | |||
</math> | |||
:<math>h_{z}=1\,</math> | |||
The infinitesimal element of volume is | |||
:<math> | |||
dV = h_\sigma h_\tau h_z=\left( \sigma^{2} + \tau^{2} \right) d\sigma d\tau dz | |||
</math> | |||
and the Laplacian equals | |||
:<math> | |||
\nabla^{2} \Phi = \frac{1}{\sigma^{2} + \tau^{2}} | |||
\left( \frac{\partial^{2} \Phi}{\partial \sigma^{2}} + | |||
\frac{\partial^{2} \Phi}{\partial \tau^{2}} \right) + | |||
\frac{\partial^{2} \Phi}{\partial z^{2}} | |||
</math> | |||
Other differential operators such as <math>\nabla \cdot \mathbf{F}</math> | |||
and <math>\nabla \times \mathbf{F}</math> can be expressed in the coordinates <math>(\sigma, \tau)</math> by substituting | |||
the scale factors into the general formulae | |||
found in [[orthogonal coordinates]]. | |||
== Parabolic cylinder harmonics == | |||
Since all of the surfaces of constant σ, τ and ''z'' are conicoid, Laplace's equation is separable in parabolic cylindrical coordinates. Using the technique of the [[separation of variables]], a separated solution to Laplace's equation may be written: | |||
:<math>V=S(\sigma)\,T(\tau)\,Z(z)</math> | |||
and Laplace's equation, divided by ''V'' , is written: | |||
:<math>\frac{1}{\sigma^2+\tau^2} | |||
\left[\frac{\ddot{S}}{S}+\frac{\ddot{T}}{T}\right]+\frac{\ddot{Z}}{Z}=0 | |||
</math> | |||
Since the ''Z'' equation is separate from the rest, we may write | |||
:<math>\frac{\ddot{Z}}{Z}=-m^2</math> | |||
where ''m'' is constant. ''Z(z)'' has the solution: | |||
:<math>Z_m(z)=A_1\,e^{imz}+A_2\,e^{-imz}\,</math> | |||
Substituting <math>-m^2</math> for <math>\ddot{Z}/Z</math> , Laplace's equation may now be written: | |||
:<math>\left[\frac{\ddot{S}}{S}+\frac{\ddot{T}}{T}\right]=m^2(\sigma^2+\tau^2)</math> | |||
We may now separate the ''S'' and ''T'' functions and introduce another constant <math>n^2</math> to obtain: | |||
:<math>\ddot{S} - (m^2\sigma^2+n^2)S=0</math> | |||
:<math>\ddot{T} - (m^2\tau^2 -n^2)T=0</math> | |||
The solutions to these equations are the [[parabolic cylinder functions]] | |||
:<math>S_{mn}(\sigma) = A_3\,y_1(n^2/2m,\sigma\sqrt{2m}) + A_4\,y_2(n^2/2m,\sigma\sqrt{2m})</math> | |||
:<math>T_{mn}(\tau) = A_5\,y_1(n^2/2m,i\tau \sqrt{2m}) + A_6\,y_2(n^2/2m,i\tau \sqrt{2m})</math> | |||
The parabolic cylinder harmonics for (m,n) are now the product of the solutions. The combination will reduce the number of constants and the general solution to Laplace's equation may be written: | |||
:<math>V(\sigma,\tau,z)=\sum_{m,n} A_{mn} S_{mn} T_{mn} Z_m\,</math> | |||
==Applications== | |||
The classic applications of parabolic cylindrical coordinates are in solving [[partial differential equations]], | |||
e.g., [[Laplace's equation]] or the [[Helmholtz equation]], for which such coordinates allow a | |||
[[separation of variables]]. A typical example would be the [[electric field]] surrounding a | |||
flat semi-infinite conducting plate. | |||
==Bibliography== | |||
*{{cite book | author = [[Philip M. Morse|Morse PM]], [[Herman Feshbach|Feshbach H]] | year = 1953 | title = Methods of Theoretical Physics, Part I | publisher = McGraw-Hill | location = New York | isbn = 0-07-043316-X|lccn=52011515 | page = 658}} | |||
*{{cite book | author = [[Henry Margenau|Margenau H]], Murphy GM | year = 1956 | title = The Mathematics of Physics and Chemistry | publisher = D. van Nostrand | location = New York | pages = 186–187 | lccn = 5510911 }} | |||
*{{cite book | author = Korn GA, Korn TM |year = 1961 | title = Mathematical Handbook for Scientists and Engineers | publisher = McGraw-Hill | location = New York | id = ASIN B0000CKZX7 | page = 181 | lccn = 5914456}} | |||
*{{cite book | author = Sauer R, Szabó I | year = 1967 | title = Mathematische Hilfsmittel des Ingenieurs | publisher = Springer Verlag | location = New York | page = 96 | lccn = 6725285}} | |||
*{{cite book | author = Zwillinger D | year = 1992 | title = Handbook of Integration | publisher = Jones and Bartlett | location = Boston, MA | isbn = 0-86720-293-9 | page = 114}} Same as Morse & Feshbach (1953), substituting ''u''<sub>''k''</sub> for ξ<sub>''k''</sub>. | |||
*{{cite book | author = Moon P, Spencer DE | year = 1988 | chapter = Parabolic-Cylinder Coordinates (μ, ν, z) | title = Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions | edition = corrected 2nd ed., 3rd print | publisher = Springer-Verlag | location = New York | pages = 21–24 (Table 1.04) | isbn = 978-0-387-18430-2}} | |||
==External links== | |||
*[http://mathworld.wolfram.com/ParabolicCylindricalCoordinates.html MathWorld description of parabolic cylindrical coordinates] | |||
{{Orthogonal coordinate systems}} | |||
[[Category:Coordinate systems]] | |||
Revision as of 04:30, 10 October 2013
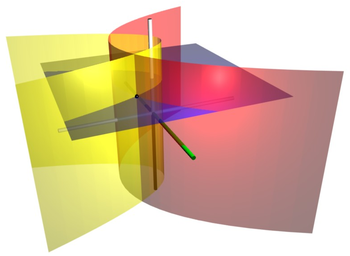
In mathematics, parabolic cylindrical coordinates are a three-dimensional orthogonal coordinate system that results from projecting the two-dimensional parabolic coordinate system in the perpendicular -direction. Hence, the coordinate surfaces are confocal parabolic cylinders. Parabolic cylindrical coordinates have found many applications, e.g., the potential theory of edges.
Basic definition
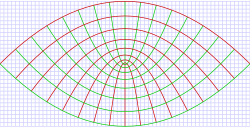
The parabolic cylindrical coordinates are defined in terms of the Cartesian coordinates (x,y,z) by:
The surfaces of constant form confocal parabolic cylinders
that open towards , whereas the surfaces of constant form confocal parabolic cylinders
that open in the opposite direction, i.e., towards . The foci of all these parabolic cylinders are located along the line defined by . The radius r has a simple formula as well
that proves useful in solving the Hamilton-Jacobi equation in parabolic coordinates for the inverse-square central force problem of mechanics; for further details, see the Laplace–Runge–Lenz vector article.
Scale factors
The scale factors for the parabolic cylindrical coordinates and are:
The infinitesimal element of volume is
and the Laplacian equals
Other differential operators such as and can be expressed in the coordinates by substituting the scale factors into the general formulae found in orthogonal coordinates.
Parabolic cylinder harmonics
Since all of the surfaces of constant σ, τ and z are conicoid, Laplace's equation is separable in parabolic cylindrical coordinates. Using the technique of the separation of variables, a separated solution to Laplace's equation may be written:
and Laplace's equation, divided by V , is written:
Since the Z equation is separate from the rest, we may write
where m is constant. Z(z) has the solution:
Substituting for , Laplace's equation may now be written:
We may now separate the S and T functions and introduce another constant to obtain:
The solutions to these equations are the parabolic cylinder functions
The parabolic cylinder harmonics for (m,n) are now the product of the solutions. The combination will reduce the number of constants and the general solution to Laplace's equation may be written:
Applications
The classic applications of parabolic cylindrical coordinates are in solving partial differential equations, e.g., Laplace's equation or the Helmholtz equation, for which such coordinates allow a separation of variables. A typical example would be the electric field surrounding a flat semi-infinite conducting plate.
Bibliography
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 Same as Morse & Feshbach (1953), substituting uk for ξk. - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534





















![{\displaystyle {\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {\ddot {S}}{S}}+{\frac {\ddot {T}}{T}}\right]+{\frac {\ddot {Z}}{Z}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99190e6afe07d230b871dd5a2f159b9cf8179d2c)




![{\displaystyle \left[{\frac {\ddot {S}}{S}}+{\frac {\ddot {T}}{T}}\right]=m^{2}(\sigma ^{2}+\tau ^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/544c991ae2342d2a4f196e566d4357f7195a7c6c)





