Chaplygin gas: Difference between revisions
en>RJHall m Diffuse the category |
en>Anrnusna No edit summary |
||
| Line 1: | Line 1: | ||
{{Orphan|date=March 2011}} | |||
The '''Sparse Matrix Converter''' is an [[AC/AC converter]] which offers a reduced number of components, a low-complexity modulation scheme, and low realization effort | |||
.<ref>J. W. Kolar, M. Baumann, F. Stögerer, F. Schafmeister, H. Ertl, “Novel Three-Phase AC-DC-AC Sparse Matrix Converter, Part I - Derivation, Basic Principle of Operation, Space Vector Modulation, Dimensioning, Part II - Experimental Analysis of the Very Sparse Matrix Converter“, in Proceedings of the 17th IEEE APEC’02, Dallas, USA, Vol. 2, pp. 777 – 791, March 10 – 14, 2002.</ref> | |||
<ref>L. Wei, T. A. Lipo, H. Chan, “Matrix Converter Topologies with Reduced Number of Switches“, in Proceedings of the VPEC’02, Blacksburg, USA, pp. 125 – 130, April 14 – 18, 2002.</ref><ref>F. Schafmeister, “Sparse und Indirekte Matrix Konverter“, PhD thesis No. 17428, ETH Zürich, Switzerland, 2007.</ref><ref>J. W. Kolar, F. Schafmeister, S. D. Round, and H. Ertl, “Novel Three-Phase AC-AC Sparse Matrix Converters“, Transactions Power Electronics, Vol. 22, No. 5, pp. 1649–1661, 2007.</ref> Invented in 2001 by Prof [[Johann W. Kolar]]<ref>J. W. Kolar, „Vorrichtung Zur Quasi-Direkten Pulsbreitengesteuerten Energieumformung Zwischen Dreiphasennetzen“, Jul. 27, 2001, Austrian Patent Application (in German), filed</ref> | |||
, sparse matrix converters avoid the multi step commutation procedure of the conventional matrix converter, improving system reliability in industrial operations. Its principal application is in highly compact integrated AC drives. | |||
==Characteristics<ref>Java-Animation of the functionality of the Sparse Matrix Converter, iPES (Interactive Power Electronics Seminar) at [http://www.ipes.ethz.ch www.ipes.ethz.ch]</ref>== | |||
*Quasi-Direct AC-AC conversion with no DC link energy storage elements | |||
*Sinusoidal input current in phase with mains voltage | |||
*Zero DC link current commutation scheme resulting in lower modulation complexity and very high reliability | |||
*Low complexity of power circuit / power modules available | |||
*Ultra-Sparse Matrix Converter, does show very low realization effort, in case unidirectional power flow can be accepted (admissible displacement of 30° the input current fundamental and input voltage, as well as for the output voltage fundamental and output current), accordingly, a possible application area would be variable speed PSM drives of low dynamics. | |||
==Topologies== | |||
===Sparse Matrix Converter=== | |||
<!-- Deleted image removed: [[Image:Sparse matrix converter.jpg|thumb|Fig 1: Topology of the sparse matrix converter | |||
<ref> J. W. Kolar, M. Baumann, F. Stögerer, F. Schafmeister, H. Ertl, “Novel Three-Phase AC-DC-AC Sparse Matrix Converter, Part I - Derivation, Basic Principle of Operation, Space Vector Modulation, Dimensioning, Part II - Experimental Analysis of the Very Sparse Matrix Converter“, in Proceedings of the 17th IEEE APEC’02, Dallas, USA, Vol. 2, pp. 777 – 791, March 10 – 14, 2002.</ref> | |||
<ref>L. Wei, T. A. Lipo, H. Chan, “Matrix Converter Topologies with Reduced Number of Switches“, in Proceedings of the VPEC’02, Blacksburg, USA, pp. 125 – 130, April 14 – 18, 2002. </ref> <ref> F. Schafmeister, “Sparse und Indirekte Matrix Konverter“, PhD thesis No. 17428, ETH Zürich, Switzerland, 2007.</ref> | |||
<ref> J. W. Kolar, F. Schafmeister, S. D. Round, and H. Ertl, “Novel Three-Phase AC-AC Sparse Matrix Converters“, Transactions Power Electronics, Vol. 22, No. 5, pp. 1649 – 1661, 2007.</ref> | |||
]] --> | |||
Characteristics of the Sparse Matrix Converter topology are 15 Transistors, 18 Diodes, and 7 Isolated Driver Potentials. Compared to the [[Direct Matrix Converter]] this topology provides identical functionality, but with a reduced number of power switches and the option of employing an improved zero DC-link current commutation scheme, which provides lower control complexity and higher safety and reliability. | |||
===Very Sparse Matrix Converter=== | |||
[[Image:Very sparse matrix.jpg|thumb|Fig 2: Topology of the very-sparse matrix.]] | |||
Characteristics of the Very Sparse Matrix Converter topology are 12 Transistors, 30 Diodes, and 10 Isolated Driver Potentials. There are no limitations in functionality compared to the Direct Matrix Converter and Sparse Matrix Converter. Compared to the Sparse Matrix Converter there are fewer transistors but higher conduction losses due to the increased number of diodes in the conduction paths. | |||
===Ultra Sparse Matrix Converter=== | |||
[[Image:Ultra sparse matrix.jpg|thumb|Fig 3: Topology of the ultra-sparse matrix.]] | |||
Characteristics of the Ultra Sparse Matrix Converter topology are 9 Transistors, 18 Diodes, and 7 Isolated Driver Potentials. The significant limitation of this converter topology compared to the Sparse Matrix Converter is the restriction of its maximal phase displacement between input voltage and input current which is restricted to ± 30°. | |||
===Multi-Step Commutation=== | |||
[[Image:Multistep commutation of sm.jpg|thumb|Fig 4: Multistep commutation of the Sparse Matrix Converter rectifier input stage.]] | |||
This is a commutation scheme, depicted in Fig. 4. For a given switching state of the rectifier input stage, the commutation of the inverter output stage has to be performed in an identical manner to the commutation of a conventional voltage dc-link converter. The basic structure of the commutating bridge legs of the Sparse Matrix Converter is shown in Fig. 4(a). The switch sequence to change the connection of the positive dc-link voltage bus p from input a to input b is shown in Fig. 4(b) and Fig. 4(c). In Fig. 4(b) the assumption is current-independent commutation with uab > 0. In Fig. 4(c) the assumption is voltage-independent commutation with i > 0. | |||
A dead time between the turn-off and turn-on of the power transistors of a bridge leg has to be implemented in order to avoid a short circuit of the dc-link voltage. To change the switching state of the Sparse Matrix Converter rectifier input stage for a given inverter switching state, one has to make sure that there is no bidirectional connection between any two input lines. This guarantees that no short-circuiting of an input line-to-line voltage can occur. Additionally a current path must be continuously provided. Therefore multistep commutation schemes, using voltage independent and current independent commutation as known for the Conventional Direct Matrix Converter | |||
<ref>P. Wheeler, J. Rodriguez, J. Clare, L. Empringham, A. Weinstein, “Matrix converters: A technology review”, IEEE Transactions on Industrial Electronics, Vol. 49, No. 2, pp. 276–288, Apr. 2002.</ref> | |||
, can be employed. | |||
===Zero DC Link Current Commutation=== | |||
[[Image:Zero dc link commutation.jpg|thumb|Fig 5: Zero DC link current commutation shown for the Sparse Matrix Converter.]] | |||
The drawback of the multistep commutation describe before is its complexity. Indirect matrix converters like the Sparse Matrix Converter provide a degree of control freedom that is not available for the Conventional Direct Matrix Converter. This can be used to simplify the complex commutation problem. It has been proposed <ref>J. Holtz, U. Boelkens, “Direct frequency converter with sinusoidal line currents for speed-variable ac motors”, IEEE Transactions on Industrial Electronics, Vol. 36, No. 4, pp. 475 – 478, Nov. 1989.</ref> to switch the inverter stage into a free-wheeling state, and then to commutate the rectifier stage with zero dc-link current. This is shown in Fig. 5. | |||
Fig. 5(a) shows the control of the power transistors in one bridge leg of the Sparse Matrix Converter. Fig. 5(b) shows the switching state sequence where s0; s7 = 1 indicates free-wheeling operation of the inverter stage. Furthermore, the dc-link current i is shown. | |||
The zero DC link current commutation scheme gives the additional benefit of a reduction in the switching losses of the input stage. One only has to ensure that no overlapping of turn-on intervals of power transistors in a bridge half occurs, because this would result in a short circuit of an input line-to-line voltage. | |||
[[Image:Characteristic voltages sparse matrix.jpg|thumb|Fig 6: Characteristic voltages and currents and switching states of the Sparse Matrix Converter during on-switching period.]] | |||
Fig 6 shows the formation of the dc-link voltage u and dc-link current i within one switching period | |||
Furthermore, it shows as an example the switching functions of the rectifier and inverter stage for <math>\phi_1</math> in interval <math>(0...\pi/6)</math>and <math>\phi_2</math> in interval <math>(0 . . . \pi/6)</math>. Input stage switching occurs at zero dc-link current. The dc-link current has a constant average value <math>\bar{i}</math> within <math>\tau_{ac}</math> and <math>\tau_{ab}</math>. The switching state functions are given as <math>s_A, s_B</math>, and <math>s_C</math>. The switching frequency ripple of <math>u_{ac} , u_{ab} , i_A</math> and <math>i_C</math> is neglected | |||
==References== | |||
{{Reflist}} | |||
{{DEFAULTSORT:Sparse Matrix Converter}} | |||
[[Category:Electronic circuits]] | |||
[[Category:Electrical power conversion]] | |||
Latest revision as of 19:33, 23 September 2013
The Sparse Matrix Converter is an AC/AC converter which offers a reduced number of components, a low-complexity modulation scheme, and low realization effort .[1] [2][3][4] Invented in 2001 by Prof Johann W. Kolar[5] , sparse matrix converters avoid the multi step commutation procedure of the conventional matrix converter, improving system reliability in industrial operations. Its principal application is in highly compact integrated AC drives.
Characteristics[6]
- Quasi-Direct AC-AC conversion with no DC link energy storage elements
- Sinusoidal input current in phase with mains voltage
- Zero DC link current commutation scheme resulting in lower modulation complexity and very high reliability
- Low complexity of power circuit / power modules available
- Ultra-Sparse Matrix Converter, does show very low realization effort, in case unidirectional power flow can be accepted (admissible displacement of 30° the input current fundamental and input voltage, as well as for the output voltage fundamental and output current), accordingly, a possible application area would be variable speed PSM drives of low dynamics.
Topologies
Sparse Matrix Converter
Characteristics of the Sparse Matrix Converter topology are 15 Transistors, 18 Diodes, and 7 Isolated Driver Potentials. Compared to the Direct Matrix Converter this topology provides identical functionality, but with a reduced number of power switches and the option of employing an improved zero DC-link current commutation scheme, which provides lower control complexity and higher safety and reliability.
Very Sparse Matrix Converter
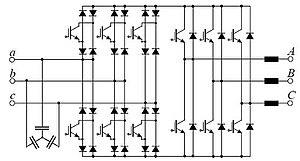
Characteristics of the Very Sparse Matrix Converter topology are 12 Transistors, 30 Diodes, and 10 Isolated Driver Potentials. There are no limitations in functionality compared to the Direct Matrix Converter and Sparse Matrix Converter. Compared to the Sparse Matrix Converter there are fewer transistors but higher conduction losses due to the increased number of diodes in the conduction paths.
Ultra Sparse Matrix Converter

Characteristics of the Ultra Sparse Matrix Converter topology are 9 Transistors, 18 Diodes, and 7 Isolated Driver Potentials. The significant limitation of this converter topology compared to the Sparse Matrix Converter is the restriction of its maximal phase displacement between input voltage and input current which is restricted to ± 30°.
Multi-Step Commutation

This is a commutation scheme, depicted in Fig. 4. For a given switching state of the rectifier input stage, the commutation of the inverter output stage has to be performed in an identical manner to the commutation of a conventional voltage dc-link converter. The basic structure of the commutating bridge legs of the Sparse Matrix Converter is shown in Fig. 4(a). The switch sequence to change the connection of the positive dc-link voltage bus p from input a to input b is shown in Fig. 4(b) and Fig. 4(c). In Fig. 4(b) the assumption is current-independent commutation with uab > 0. In Fig. 4(c) the assumption is voltage-independent commutation with i > 0.
A dead time between the turn-off and turn-on of the power transistors of a bridge leg has to be implemented in order to avoid a short circuit of the dc-link voltage. To change the switching state of the Sparse Matrix Converter rectifier input stage for a given inverter switching state, one has to make sure that there is no bidirectional connection between any two input lines. This guarantees that no short-circuiting of an input line-to-line voltage can occur. Additionally a current path must be continuously provided. Therefore multistep commutation schemes, using voltage independent and current independent commutation as known for the Conventional Direct Matrix Converter [7] , can be employed.
Zero DC Link Current Commutation

The drawback of the multistep commutation describe before is its complexity. Indirect matrix converters like the Sparse Matrix Converter provide a degree of control freedom that is not available for the Conventional Direct Matrix Converter. This can be used to simplify the complex commutation problem. It has been proposed [8] to switch the inverter stage into a free-wheeling state, and then to commutate the rectifier stage with zero dc-link current. This is shown in Fig. 5.
Fig. 5(a) shows the control of the power transistors in one bridge leg of the Sparse Matrix Converter. Fig. 5(b) shows the switching state sequence where s0; s7 = 1 indicates free-wheeling operation of the inverter stage. Furthermore, the dc-link current i is shown.
The zero DC link current commutation scheme gives the additional benefit of a reduction in the switching losses of the input stage. One only has to ensure that no overlapping of turn-on intervals of power transistors in a bridge half occurs, because this would result in a short circuit of an input line-to-line voltage.

Fig 6 shows the formation of the dc-link voltage u and dc-link current i within one switching period Furthermore, it shows as an example the switching functions of the rectifier and inverter stage for in interval and in interval . Input stage switching occurs at zero dc-link current. The dc-link current has a constant average value within and . The switching state functions are given as , and . The switching frequency ripple of and is neglected
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
- ↑ J. W. Kolar, M. Baumann, F. Stögerer, F. Schafmeister, H. Ertl, “Novel Three-Phase AC-DC-AC Sparse Matrix Converter, Part I - Derivation, Basic Principle of Operation, Space Vector Modulation, Dimensioning, Part II - Experimental Analysis of the Very Sparse Matrix Converter“, in Proceedings of the 17th IEEE APEC’02, Dallas, USA, Vol. 2, pp. 777 – 791, March 10 – 14, 2002.
- ↑ L. Wei, T. A. Lipo, H. Chan, “Matrix Converter Topologies with Reduced Number of Switches“, in Proceedings of the VPEC’02, Blacksburg, USA, pp. 125 – 130, April 14 – 18, 2002.
- ↑ F. Schafmeister, “Sparse und Indirekte Matrix Konverter“, PhD thesis No. 17428, ETH Zürich, Switzerland, 2007.
- ↑ J. W. Kolar, F. Schafmeister, S. D. Round, and H. Ertl, “Novel Three-Phase AC-AC Sparse Matrix Converters“, Transactions Power Electronics, Vol. 22, No. 5, pp. 1649–1661, 2007.
- ↑ J. W. Kolar, „Vorrichtung Zur Quasi-Direkten Pulsbreitengesteuerten Energieumformung Zwischen Dreiphasennetzen“, Jul. 27, 2001, Austrian Patent Application (in German), filed
- ↑ Java-Animation of the functionality of the Sparse Matrix Converter, iPES (Interactive Power Electronics Seminar) at www.ipes.ethz.ch
- ↑ P. Wheeler, J. Rodriguez, J. Clare, L. Empringham, A. Weinstein, “Matrix converters: A technology review”, IEEE Transactions on Industrial Electronics, Vol. 49, No. 2, pp. 276–288, Apr. 2002.
- ↑ J. Holtz, U. Boelkens, “Direct frequency converter with sinusoidal line currents for speed-variable ac motors”, IEEE Transactions on Industrial Electronics, Vol. 36, No. 4, pp. 475 – 478, Nov. 1989.