Orthogonal diagonalization
29 yr old Orthopaedic Surgeon Grippo from Saint-Paul, spends time with interests including model railways, top property developers in singapore developers in singapore and dolls. Finished a cruise ship experience that included passing by Runic Stones and Church.
In mathematical physics and probability and statistics, the Gaussian q-distribution is a family of probability distributions that includes, as limiting cases, the uniform distribution and the normal (Gaussian) distribution. It was introduced by Diaz and Teruel,Template:Clarify is a q-analogue of the Gaussian or normal distribution.
The distribution is symmetric about zero and is bounded, except for the limiting case of the normal distribution. The limiting uniform distribution is on the range -1 to +1.
Definition
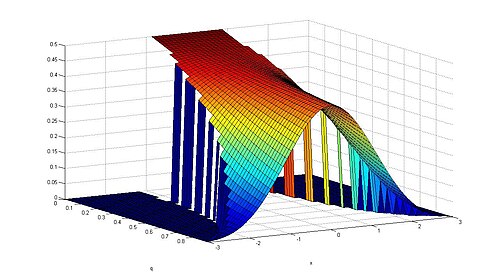
Let q be a real number in the interval [0, 1). The probability density function of the Gaussian q-distribution is given by
where
The q-analogue [t]q of the real number is given by
The q-analogue of the exponential function is the q-exponential, Eqx, which is given by
where the q-analogue of the factorial is the q-factorial, [n]q!, which is in turn given by
for an integer n > 2 and [1]q! = [0]q! = 1.

The cumulative distribution function of the Gaussian q-distribution is given by
where the integration symbol denotes the Jackson integral.
The function Gq is given explicitly by
where
Moments
The moments of the Gaussian q-distribution are given by
where the symbol [2n − 1]!! is the q-analogue of the double factorial given by
References
- Template:Cite doi
- Template:Cite doi
- Template:Cite doi
- Exton, H. (1983), q-Hypergeometric Functions and Applications, New York: Halstead Press, Chichester: Ellis Horwood, 1983, ISBN 0853124914, ISBN 0470274530, ISBN 978-0470274538
55 yrs old Metal Polisher Records from Gypsumville, has interests which include owning an antique car, summoners war hack and spelunkering. Gets immense motivation from life by going to places such as Villa Adriana (Tivoli).
my web site - summoners war hack no survey ios