Portal:Systems science/Article/4

The moment distribution method (not to be confused with moment redistribution) is a structural analysis method for statically indeterminate beams and frames developed by Hardy Cross. It was published in 1930 in an ASCE journal.^[1] The method only accounts for flexural effects and ignores axial and shear effects. From the 1930s until computers began to be widely used in the design and analysis of structures, the moment distribution method was the most widely practiced method.

Introduction

In the moment distribution method, every joint of the structure to be analysed is fixed so as to develop the fixed-end moments. Then each fixed joint is sequentially released and the fixed-end moments (which by the time of release are not in equilibrium) are distributed to adjacent members until equilibrium is achieved. The moment distribution method in mathematical terms can be demonstrated as the process of solving a set of simultaneous equations by means of iteration.

The moment distribution method falls into the category of displacement method of structural analysis.

Implementation

In order to apply the moment distribution method to analyse a structure, the following things must be considered.

Fixed end moments

Fixed end moments are the moments produced at member ends by external loads when the joints are fixed.

Flexural stiffness

The flexural stiffness (EI/L) of a member is represented as the product of the modulus of elasticity (E) and the second moment of area (I) divided by the length (L) of the member. What is needed in the moment distribution method is not the exact value but the ratio of flexural stiffness of all members.

Distribution factors

When a joint is released and begins to rotate under the unbalanced moment, resisting forces develop at each member framed together at the joint. Although the total resistance is equal to the unbalanced moment, the magnitudes of resisting forces developed at each member differ by the members' flexural stiffness. Distribution factors can be defined as the proportions of the unbalanced moments carried by each of the members. In mathematical terms, distribution factor of member $k$ framed at joint $j$ is given as:

D_{j k} = \frac{\frac{E_{k} I_{k}}{L_{k}}}{\sum_{i = 1}^{i = n} \frac{E_{i} I_{i}}{L_{i}}}

where n is the number of members framed at the joint.

Carryover factors

When a joint is released, balancing moment occurs to counterbalance the unbalanced moment which is initially the same as the fixed-end moment. This balancing moment is then carried over to the member's other end. The ratio of the carried-over moment at the other end to the fixed-end moment of the initial end is the carryover factor.

Determination of carryover factors

Let one end (end A) of a fixed beam be released and applied a moment $M_{A}$ while the other end (end B) remains fixed. This will cause end A to rotate through an angle $θ_{A}$ . Once the magnitude of $M_{B}$ developed at end B is found, the carryover factor of this member is given as the ratio of $M_{B}$ over $M_{A}$ :

C_{A B} = \frac{M_{B}}{M_{A}}

In case of a beam of length L with constant cross-section whose flexural rigidity is $E I$ ,

M_{A} = 4 \frac{E I}{L} θ_{A} + 2 \frac{E I}{L} θ_{B} = 4 \frac{E I}{L} θ_{A}

M_{B} = 2 \frac{E I}{L} θ_{A} + 4 \frac{E I}{L} θ_{B} = 2 \frac{E I}{L} θ_{A}

therefore the carryover factor

C_{A B} = \frac{M_{B}}{M_{A}} = \frac{1}{2}

Sign convention

Once a sign convention has been chosen, it has to be maintained for the whole structure. The traditional engineer's sign convention is not used in the calculations of the moment distribution method although the results can be expressed in the conventional way. In the BMD case, the left side moment is clockwise direction and other is anticlockwise direction so the bending is positive and is called sagging.

Framed structures

Framed structures with or without sidesway can be analysed using the moment distribution method.

Example

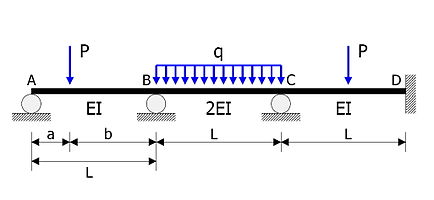
The statically indeterminate beam shown in the figure is to be analysed.

Members AB, BC, CD have the same length $L = 10 m$ .
Flexural rigidities are EI, 2EI, EI respectively.
Concentrated load of magnitude $P = 10 k N$ acts at a distance $a = 3 m$ from the support A.
Uniform load of intensity $q = 1 k N / m$ acts on BC.
Member CD is loaded at its midspan with a concentrated load of magnitude $P = 15 k N$ .

In the following calculations, counterclockwise moments are positive.

Fixed end moments

DTZ's public sale group in Singapore auctions all forms of residential, workplace and retail properties, outlets, homes, lodges, boarding homes, industrial buildings and development websites. Auctions are at present held as soon as a month.

We will not only get you a property at a rock-backside price but also in an space that you've got longed for. You simply must chill out back after giving us the accountability. We will assure you 100% satisfaction. Since we now have been working in the Singapore actual property market for a very long time, we know the place you may get the best property at the right price. You will also be extremely benefited by choosing us, as we may even let you know about the precise time to invest in the Singapore actual property market.

The Hexacube is offering new ec launch singapore business property for sale Singapore investors want to contemplate. Residents of the realm will likely appreciate that they'll customize the business area that they wish to purchase as properly. This venture represents one of the crucial expansive buildings offered in Singapore up to now. Many investors will possible want to try how they will customise the property that they do determine to buy by means of here. This location has offered folks the prospect that they should understand extra about how this course of can work as well.

Singapore has been beckoning to traders ever since the value of properties in Singapore started sky rocketing just a few years again. Many businesses have their places of work in Singapore and prefer to own their own workplace area within the country once they decide to have a everlasting office. Rentals in Singapore in the corporate sector can make sense for some time until a business has discovered a agency footing. Finding Commercial Property Singapore takes a variety of time and effort but might be very rewarding in the long term.

is changing into a rising pattern among Singaporeans as the standard of living is increasing over time and more Singaporeans have abundance of capital to invest on properties. Investing in the personal properties in Singapore I would like to applaud you for arising with such a book which covers the secrets and techniques and tips of among the profitable Singapore property buyers. I believe many novice investors will profit quite a bit from studying and making use of some of the tips shared by the gurus." – Woo Chee Hoe Special bonus for consumers of Secrets of Singapore Property Gurus Actually, I can't consider one other resource on the market that teaches you all the points above about Singapore property at such a low value. Can you? Condominium For Sale (D09) – Yong An Park For Lease

In 12 months 2013, c ommercial retails, shoebox residences and mass market properties continued to be the celebrities of the property market. Models are snapped up in report time and at document breaking prices. Builders are having fun with overwhelming demand and patrons need more. We feel that these segments of the property market are booming is a repercussion of the property cooling measures no.6 and no. 7. With additional buyer's stamp responsibility imposed on residential properties, buyers change their focus to commercial and industrial properties. I imagine every property purchasers need their property funding to understand in value.

M_{A B}^{f} = - \frac{P b^{2} a}{L^{2}} = - \frac{10 \times 7^{2} \times 3}{1 0^{2}} = - 14.700 k N \cdot m

M_{B A}^{f} = \frac{P a^{2} b}{L^{2}} = \frac{10 \times 3^{2} \times 7}{1 0^{2}} = + 6.300 k N \cdot m

M_{B C}^{f} = - \frac{q L^{2}}{12} = - \frac{1 \times 1 0^{2}}{12} = - 8.333 k N \cdot m

M_{C B}^{f} = \frac{q L^{2}}{12} = \frac{1 \times 1 0^{2}}{12} = + 8.333 k N \cdot m

M_{C D}^{f} = - \frac{P L}{8} = - \frac{10 \times 10}{8} = - 12.500 k N \cdot m

M_{D C}^{f} = \frac{P L}{8} = \frac{10 \times 10}{8} = + 12.500 k N \cdot m

Flexural stiffness and distribution factors

The flexural stiffness of members AB, BC and CD are $\frac{3 E I}{L}$ , $\frac{4 \times 2 E I}{L}$ and $\frac{4 E I}{L}$ , respectively. Therefore, expressing the results in repeating decimal notation:

D_{B A} = \frac{\frac{3 E I}{L}}{\frac{3 E I}{L} + \frac{4 \times 2 E I}{L}} = \frac{\frac{3}{10}}{\frac{3}{10} + \frac{8}{10}} = \frac{3}{11} = 0 . (27)

D_{B C} = \frac{\frac{4 \times 2 E I}{L}}{\frac{3 E I}{L} + \frac{4 \times 2 E I}{L}} = \frac{\frac{8}{10}}{\frac{3}{10} + \frac{8}{10}} = \frac{8}{11} = 0 . (72)

D_{C B} = \frac{\frac{4 \times 2 E I}{L}}{\frac{4 \times 2 E I}{L} + \frac{4 E I}{L}} = \frac{\frac{8}{10}}{\frac{8}{10} + \frac{4}{10}} = \frac{8}{12} = 0 . (67)

D_{C D} = \frac{\frac{4 E I}{L}}{\frac{4 \times 2 E I}{L} + \frac{4 E I}{L}} = \frac{\frac{4}{10}}{\frac{8}{10} + \frac{4}{10}} = \frac{4}{12} = 0 . (33)

The distribution factors of joints A and D are $D_{A B} = 1$ and $D_{D C} = 0$ .

Carryover factors

The carryover factors are $\frac{1}{2}$ , except for the carryover factor from D (fixed support) to C which is zero.

Moment distribution


	Joint	A		Joint	B		Joint	C		Joint	D
Distrib. factors	0	1		0.2727	0.7273		0.6667	0.3333		0	0
Fixed-end moments		-14.700		+6.300	-8.333		+8.333	-12.500		+12.500
Step 1		+14.700	→	+7.350
Step 2				-1.450	-3.867	→	-1.934
Step 3					+2.034	←	+4.067	+2.034	→	+1.017
Step 4				-0.555	-1.479	→	-0.739
Step 5					+0.246	←	+0.493	+0.246	→	+0.123
Step 6				-0.067	-0.179	→	-0.090
Step 7					+0.030	←	+0.060	+0.030	→	+0.015
Step 8				-0.008	-0.022	→	-0.011
Step 9					+0.004	←	+0.007	+0.004	→	+0.002
Step 10				0.001	0.003
Sum of moments		0		+11.569	-11.569		+10.186	-10.186		+13.657

Numbers in grey are balanced moments; arrows ( → / ← ) represent the carry-over of moment from one end to the other end of a member.

Step 1

As joint A is released, balancing moment of magnitude equal to the fixed end moment

M_{A B}^{f} = 14.700 k N m

develops and is carried-over from joint A to joint B.

Step 2

The unbalanced moment at joint B now is the summation of the fixed end moments

M_{B A}^{f}

,

M_{B C}^{f}

and the carry-over moment from joint A. This unbalanced moment is distributed to members BA and BC in accordance with the distribution factors

D_{B A} = 0.2727

and

D_{B C} = 0.7273

. Step 2 ends with carry-over of balanced moment

M_{B C} = 3.867 k N m

to joint C. Joint A is a roller support which has no rotational restraint, so moment carryover from joint B to joint A is zero.

Step 3

The unbalanced moment at joint C now is the summation of the fixed end moments

M_{C B}^{f}

,

M_{C D}^{f}

and the carryover moment from joint B. As in the previous step, this unbalanced moment is distributed to each member and then carried over to joint C and back to joint B. Joint D is a fixed support and carried-over moments to this joint will not be distributed nor be carried over to joint C.

Step 4

Joint B still has unbalanced moment which was carried over from joint C in step 3. Joint B is released once again to induce moment distribution and to achieve equilibrium.

Steps 5 - 10

Joints are released and fixed again until every joint has unbalanced moments of size zero or neglectably small in required precision. Arithmetically summing all moments in each respective columns gives the final moment values.

Result

Moments at joints determined by the moment distribution method

M_{A} = 0 k N \cdot m

M_{B} = - 11.569 k N \cdot m

M_{C} = 10.186 k N \cdot m

M_{D} = - 13.657 k N \cdot m

The conventional engineer's sign convention is used here, i.e. positive moments cause elongation at the bottom part of a beam member.

For comparison purposes, the following are the results generated using a matrix method. Note that in the analysis above, the iterative process was carried to >0.01 precision. The fact that the matrix analysis results and the moment distribution analysis results match to 0.001 precision is mere coincidence.

Moments at joints determined by the matrix method

M_{A} = 0 k N \cdot m

M_{B} = - 11.569 k N \cdot m

M_{C} = - 10.186 k N \cdot m

M_{D} = - 13.657 k N \cdot m

The complete shear and bending moment diagrams are as shown. Note that the moment distribution method only determines the moments at the joints. Developing complete bending moment diagrams require additional calculations using the determined joint moments and internal section equilibrium.

SFD and BMD

Result via displacements method

As the Hardy Cross method provides only approximate results, with a margin of error inversely proportionate to the number of iterations, it is importantPotter or Ceramic Artist Truman Bedell from Rexton, has interests which include ceramics, best property developers in singapore developers in singapore and scrabble. Was especially enthused after visiting Alejandro de Humboldt National Park. to have an idea of how accurate this method might be. With this in mind, here is the result obtained by using an exact method: the displacement method

For this, the displacements method equation assumes the following form:

$[K] {d} = {- f}$

For the structure described in this example, the stiffness matrix is as follows:

$[K] = [\begin{matrix} 3 \frac{E I}{L} + 4 \frac{2 E I}{L} & 2 \frac{2 E I}{L} \\ 2 \frac{2 E I}{L} & 4 \frac{2 E I}{L} + 4 \frac{E I}{L} \end{matrix}]$

The equivalent nodal force vector:

${f}^{T} = {- P \frac{a b (L + a)}{2 L^{2}} + q \frac{L^{2}}{12}, - q \frac{L^{2}}{12} + P \frac{L}{8}}$

Replacing the values presented above in the equation and solving it for ${d}$ leads to the following result:

${d}^{T} = {6.9368; - 5.7845}$

Hence, the moments evaluated in node B are as follows:

$M_{B A} = 3 \frac{E I}{L} d_{1} - P \frac{a b (L + a)}{2 L^{2}} = - 11.569$

$M_{B C} = - 4 \frac{2 E I}{L} d_{1} - 2 \frac{2 E I}{L} d_{2} - q \frac{L^{2}}{12} = - 11.569$

The moments evaluated in node C are as follows:

$M_{C B} = 2 \frac{2 E I}{L} d_{1} + 4 \frac{2 E I}{L} d_{2} - q \frac{L^{2}}{12} = - 10.186$

$M_{C D} = - 4 \frac{E I}{L} d_{2} - P \frac{L}{8} = - 10.186$

Notes

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.

References

20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534

External links

↑ Template:Cite news

[asce1-1] Template:Cite news

[1]

Portal:Systems science/Article/4

Contents

Introduction

Implementation

Fixed end moments

Flexural stiffness

Distribution factors

Carryover factors

Determination of carryover factors

Sign convention

Framed structures

Example

Fixed end moments

Flexural stiffness and distribution factors

Carryover factors

Moment distribution

Result

Result via displacements method

Notes

See also

References

External links

Navigation menu

Portal:Systems science/Article/4

Introduction

Implementation

Fixed end moments

Flexural stiffness

Distribution factors

Carryover factors

Determination of carryover factors

Sign convention

Framed structures

Example

Fixed end moments

Flexural stiffness and distribution factors

Carryover factors

Moment distribution

Result

Result via displacements method

Notes

See also

References

External links

Navigation menu

Search