Lambert summation

The Steiner ellipse of an isosceles triangle

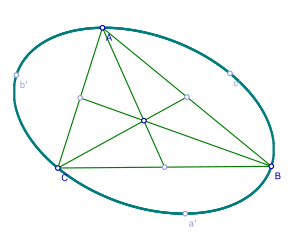
In geometry, the Steiner ellipse, also called the Steiner circumellipse to distinguish it from the Steiner inellipse, is the unique ellipse that touches a given triangle at its vertices and whose center is the triangle's centroid. Named after Jakob Steiner, it is an example of a circumconic. By comparison the circumcircle of a triangle is another circumconic that touches the triangle at its vertices, but is not centered at the triangle's centroid unless the triangle is equilateral.

The area of the Steiner ellipse equals the area of the triangle times ${\frac {4\pi }{3{\sqrt {3}}}},$ and hence is 4 times the area of the Steiner inellipse. The Steiner ellipse has the least area of any ellipse circumscribed about the triangle.

References

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.