Dilution of precision (GPS)
Burgers' equation is a fundamental partial differential equation from fluid mechanics. It occurs in various areas of applied mathematics, such as modeling of gas dynamics and traffic flow. It is named for Johannes Martinus Burgers (1895–1981).
For a given velocity u and viscosity coefficient , the general form of Burgers' equation (also known as viscous Burgers' equation) is:
When , Burgers' equation becomes the inviscid Burgers' equation:
which is a prototype for equations for which the solution can develop discontinuities (shock waves). The previous equation is the 'advection form' of the Burgers' equation. The 'conservation form' is:
Solution
Inviscid Burgers' equation
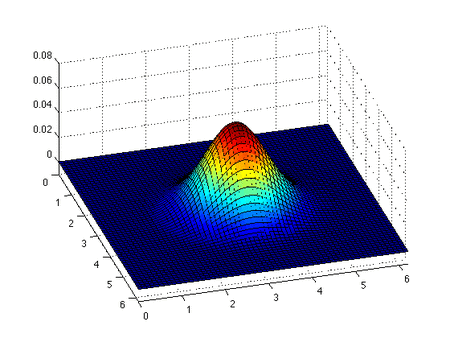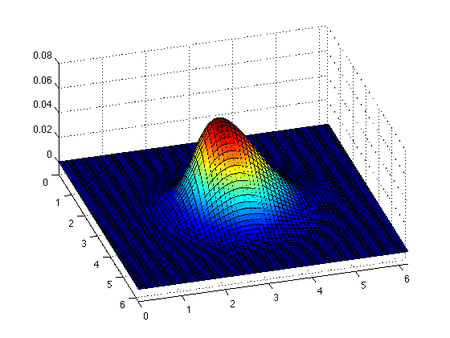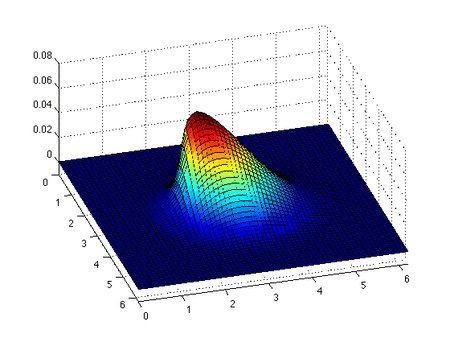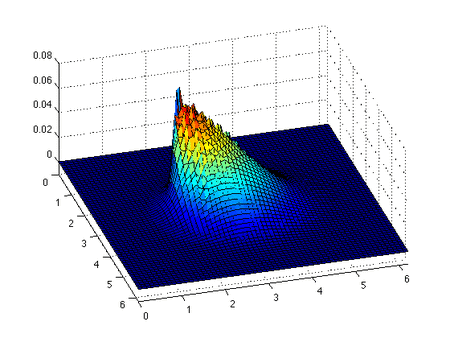
The inviscid Burgers' equation is a first order partial differential equation (PDE). Its solution can be constructed by the method of characteristics. This method yields that if is a solution of the ordinary differential equation
then is constant as a function of . Hence is a solution of the system of ordinary equations:
The solutions of this system are given in terms of the initial values by:
Substitute , then . Now the system becomes
Conclusion:
This is an implicit relation that determines the solution of the inviscid Burgers' equation provided characteristics don't intersect. If the characteristics do intersect, then a classical solution to the PDE does not exist.
Viscous Burgers' equation
The viscous Burgers' equation can be linearized by the Cole–Hopf transformation
which turns it into the equation
which can be rewritten as
with f(t) an arbitrary function. Assuming it vanishes, we get the diffusion equation
This allows one to solve an initial value problem:
References
External links
- Burgers' Equation at EqWorld: The World of Mathematical Equations.
- Burgers' Equation at NEQwiki, the nonlinear equations encyclopedia.
- Burgers shock-waves and sound in a 2D microfluidic droplets ensemble Phys. Rev. Lett. 103, 114502 (2009).