Cartan decomposition: Difference between revisions
en>Mark viking Added wl |
|||
| Line 1: | Line 1: | ||
[[Image:Hyperbolic sector.svg|200px|right]] | |||
A '''hyperbolic sector''' is a region of the [[Cartesian plane]] {(''x'',''y'')} bounded by rays from the origin to two points (''a'', 1/''a'') and (''b'', 1/''b'') and by the [[hyperbola]] ''xy'' = 1. | |||
A hyperbolic sector in standard position has ''a'' = 1 and ''b'' > 1 . | |||
==Area== | |||
The [[area]] of a hyperbolic sector in standard position is [[natural logarithm | log<sub>e</sub>]] ''b'' . | |||
Proof: Integrate under 1/''x'' from 1 to ''b'', add triangle {(0, 0), (1, 0), (1, 1)}, and subtract triangle {(0, 0), (''b'', 0), (''b'', 1/''b'')}. | |||
<ref>V.G. Ashkinuse & [[Isaak Yaglom]] (1962) ''Ideas and Methods of Affine and Projective Geometry'' (in [[Russian language|Russian]]), page 151, Ministry of Education, Moscow</ref> | |||
When in standard position, a hyperbolic sector corresponds to a positive [[hyperbolic angle]]. | |||
==Hyperbolic triangle== | |||
[[File:Cartesian hyperbolic triangle.svg|right|250px|thumb|'''Hyperbolic triangle''' (yellow) and [[hyperbolic sector]] (red) corresponding to [[hyperbolic angle]] ''u'', to the [[rectangular hyperbola]] (equation ''y'' = 1/''x''). The legs of the triangle are √2 times the [[Hyperbolic function|hyperbolic cosine and sine functions]].]] | |||
When in standard position, a hyperbolic sector determines a '''hyperbolic triangle''', the [[right triangle]] with one [[vertex (geometry)|vertex]] at the origin, base on the diagonal ray ''y'' = ''x'', and third vertex on the [[hyperbola]] | |||
:<math>xy=1.\,</math> | |||
The length of the base of such a triangle is | |||
:<math>\sqrt 2 \cosh u,\,</math> | |||
and the [[altitude (triangle)|altitude]] is | |||
:<math>\sqrt 2 \sinh u,\,</math> | |||
where ''u'' is the appropriate [[hyperbolic angle]]. | |||
The analogy between circular and hyperbolic functions was described by [[Augustus De Morgan]] in his ''Trigonometry and Double Algebra'' (1849).<ref>Augustus De Morgan (1849) [http://books.google.com/books?id=7UwEAAAAQAAJ ''Trigonometry and Double Algebra''], Chapter VI: "On the connection of common and hyperbolic trigonometry"</ref> [[William Burnside]] used such triangles, projecting from a point on the hyperbola ''xy'' = 1 onto the main diagonal, in his article "Note on the addition theorem for hyperbolic functions".<ref>William Burnside (1890) [[Messenger of Mathematics]] 20:145–8, see diagram page 146</ref> | |||
==Hyperbolic logarithm== | |||
[[Image:hyperbola E.svg|thumb|Unit area for ''x'' = e]] | |||
Students of [[integral calculus]] know that f(''x'') = ''x''<sup>p</sup> has an algebraic [[antiderivative]] except in the case p = −1 corresponding to the quadrature of the hyperbola. The other cases are given by [[Cavalieri's quadrature formula]]. Whereas quadrature of the parabola had been accomplished by [[Archimedes]] in the 3rd century BC ([[The Quadrature of the Parabola]]), the hyperbolic quadrature required the invention of a new function: [[Gregoire de Saint-Vincent]] addressed the problem of computing the area of a hyperbolic sector. His findings led to the [[natural logarithm]] function, once called the ''hyperbolic logarithm'' since it is obtained by integrating, or finding the area, under the hyperbola. | |||
The natural logarithm is a [[transcendental function]], an entity beyond the class of [[algebraic function]]s. Evidently transcendental functions are necessary in integral calculus. | |||
==Hyperbolic geometry== | |||
{{Main|Hyperbolic geometry}} | |||
When [[Felix Klein]] wrote his book on [[non-Euclidean geometry]] in 1928, he provided a foundation for the subject by reference to [[projective geometry]]. To establish hyperbolic measure on a line, he noted that the area of a hyperbolic sector provided visual illustration of the concept.<ref>[[Felix Klein]] (1928) ''Vorlesungen über Nicht-Euklidische Geometrie'', p. 173, figure 113, [[Julius Springer]], Berlin</ref> | |||
Hyperbolic sectors can also be drawn to the hyperbola <math>y = \sqrt{1 + x^2}</math>. The area of such hyperbolic sectors has been used to define hyperbolic distance in a geometry [[textbook]].<ref>Jürgen Richter-Gebert (2011) ''Perspectives on Projective Geometry'', p. 385, ISBN 9783642172854 {{MR|id=2791970}}</ref> | |||
== See also == | |||
* [[Squeeze mapping]] | |||
==References== | |||
{{reflist}} | |||
[[Category:Area]] | |||
[[Category:Elementary geometry]] | |||
[[Category:Integral calculus]] | |||
[[Category:Logarithms]] | |||
Revision as of 01:44, 12 January 2014
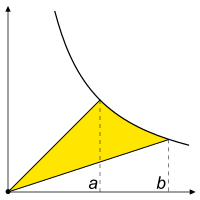
A hyperbolic sector is a region of the Cartesian plane {(x,y)} bounded by rays from the origin to two points (a, 1/a) and (b, 1/b) and by the hyperbola xy = 1.
A hyperbolic sector in standard position has a = 1 and b > 1 .
Area
The area of a hyperbolic sector in standard position is loge b .
Proof: Integrate under 1/x from 1 to b, add triangle {(0, 0), (1, 0), (1, 1)}, and subtract triangle {(0, 0), (b, 0), (b, 1/b)}. [1]
When in standard position, a hyperbolic sector corresponds to a positive hyperbolic angle.
Hyperbolic triangle

When in standard position, a hyperbolic sector determines a hyperbolic triangle, the right triangle with one vertex at the origin, base on the diagonal ray y = x, and third vertex on the hyperbola
The length of the base of such a triangle is
and the altitude is
where u is the appropriate hyperbolic angle.
The analogy between circular and hyperbolic functions was described by Augustus De Morgan in his Trigonometry and Double Algebra (1849).[2] William Burnside used such triangles, projecting from a point on the hyperbola xy = 1 onto the main diagonal, in his article "Note on the addition theorem for hyperbolic functions".[3]
Hyperbolic logarithm

Students of integral calculus know that f(x) = xp has an algebraic antiderivative except in the case p = −1 corresponding to the quadrature of the hyperbola. The other cases are given by Cavalieri's quadrature formula. Whereas quadrature of the parabola had been accomplished by Archimedes in the 3rd century BC (The Quadrature of the Parabola), the hyperbolic quadrature required the invention of a new function: Gregoire de Saint-Vincent addressed the problem of computing the area of a hyperbolic sector. His findings led to the natural logarithm function, once called the hyperbolic logarithm since it is obtained by integrating, or finding the area, under the hyperbola.
The natural logarithm is a transcendental function, an entity beyond the class of algebraic functions. Evidently transcendental functions are necessary in integral calculus.
Hyperbolic geometry
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. When Felix Klein wrote his book on non-Euclidean geometry in 1928, he provided a foundation for the subject by reference to projective geometry. To establish hyperbolic measure on a line, he noted that the area of a hyperbolic sector provided visual illustration of the concept.[4]
Hyperbolic sectors can also be drawn to the hyperbola . The area of such hyperbolic sectors has been used to define hyperbolic distance in a geometry textbook.[5]
See also
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
- ↑ V.G. Ashkinuse & Isaak Yaglom (1962) Ideas and Methods of Affine and Projective Geometry (in Russian), page 151, Ministry of Education, Moscow
- ↑ Augustus De Morgan (1849) Trigonometry and Double Algebra, Chapter VI: "On the connection of common and hyperbolic trigonometry"
- ↑ William Burnside (1890) Messenger of Mathematics 20:145–8, see diagram page 146
- ↑ Felix Klein (1928) Vorlesungen über Nicht-Euklidische Geometrie, p. 173, figure 113, Julius Springer, Berlin
- ↑ Jürgen Richter-Gebert (2011) Perspectives on Projective Geometry, p. 385, ISBN 9783642172854 Template:MR



