Gδ set: Difference between revisions
en>ZéroBot m r2.7.1) (Robot: Adding ja:Gδ集合 |
en>Melchoir |
||
| Line 1: | Line 1: | ||
{{no footnotes|date=February 2013}} | |||
In [[mathematics]], in the study of [[dynamical system]]s, an '''orbit''' is a collection of points related by the [[evolution function]] of the dynamical system. The orbit is a subset of the [[Phase space (dynamical system)|phase space]] and the set of all orbits is a [[partition (set theory)|partition]] of the phase space, that is different orbits do not intersect in the phase space. Understanding the properties of orbits by using [[Topological dynamics|topological methods]] is one of the objectives of the modern theory of dynamical systems. | |||
For [[discrete-time dynamical system]]s the orbits are [[sequence]]s, for [[real dynamical system]]s the orbits are [[curve]]s and for [[holomorphic function|holomorphic]] dynamical systems the orbits are [[Riemann surface]]s. | |||
== Definition == | |||
[[File:Simple Harmonic Motion Orbit.gif|right|thumb|300px|Diagram showing the periodic orbit of a mass-spring system in [[simple harmonic motion]]. (Here the velocity and position axes have been reversed from the standard convention in order to align the two diagrams)]] | |||
Given a dynamical system (''T'', ''M'', Φ) with ''T'' a group, M a set and Φ the evolution function | |||
:<math>\Phi: U \to M</math> where <math>U \subset T \times M</math> | |||
we define | |||
:<math>I(x):=\{t \in T : (t,x) \in U \},</math> | |||
then the set | |||
:<math>\gamma_x:=\{\Phi(t,x) : t \in I(x)\} \subset M</math> | |||
is called '''orbit''' through ''x''. An orbit which consists of a single point is called '''constant orbit'''. A non-constant orbit is called '''closed''' or '''periodic''' if there exists a ''t'' in ''T'' so that | |||
:<math>\Phi(t, x) = x \,</math> | |||
for every point ''x'' on the orbit. | |||
=== Real dynamical system === | |||
Given a real dynamical system (''R'', ''M'', Φ), ''I''(''x'')) is an open interval in the [[real number]]s, that is <math>I(x) = (t_x^- , t_x^+)</math>. For any ''x'' in ''M'' | |||
:<math>\gamma_{x}^{+} := \{\Phi(t,x) : t \in (0,t_x^+)\}</math> | |||
is called '''positive semi-orbit''' through ''x'' and | |||
:<math>\gamma_{x}^{-} := \{\Phi(t,x) : t \in (t_x^-,0)\}</math> | |||
is called '''negative semi-orbit''' through ''x''. | |||
=== Discrete time dynamical system === | |||
For discrete time dynamical system : | |||
'''forward''' orbit of x is a set : | |||
:<math> \gamma_{x}^{+} \ \overset{\underset{\mathrm{def}}{}}{=} \ \{ \Phi(t,x) : t \ge 0 \} \,</math> | |||
'''backward''' orbit of x is a set : | |||
:<math>\gamma_{x}^{-} \ \overset{\underset{\mathrm{def}}{}}{=} \ \{\Phi(-t,x) : t \ge 0 \} \,</math> | |||
and '''orbit''' of x is a set : | |||
:<math>\gamma_{x} \ \overset{\underset{\mathrm{def}}{}}{=} \ \gamma_{x}^{-} \cup \gamma_{x}^{+} \,</math> | |||
where : | |||
* <math>\Phi\,</math> is an evolution function <math>\Phi : X \to X \,</math> which is here an [[iterated function]], | |||
* set <math>X\,</math> is '''dynamical space''', | |||
*<math>t\,</math> is number of iteration, which is [[natural number]] and <math>t \in T \,</math> | |||
*<math>x\, </math> is initial state of system and <math>x \in X \,</math> | |||
Usually different notation is used : | |||
*<math>\Phi(t,x)\,</math> is noted as <math>\Phi^{t}(x)\,</math> | |||
*<math>x_t = \Phi^{t}(x)\,</math> with <math>x_0 \,</math> is a <math>x \,</math> from above notation. | |||
=== General dynamical system === | |||
For general dynamical system, especially in homogeneous dynamics, when one have a "nice" group <math>G</math> acting on a probability space <math>X</math> in a measure-preserving way, an orbit <math>G.x \subset X</math> will be called periodic (or equivalently, closed orbit) if the stabilizer <math>Stab_{G}(x)</math> is a lattice inside <math>G</math>. | |||
In addition, a related term is bounded orbit, when the set <math>G.x</math> is pre-compact inside <math>X</math>. | |||
The classification of orbits can lead to interesting questions with relations to other mathematical areas, for example the Oppenheim conjecture (proved by Margulis) and the Littlewood conjecture (partially proved by Lindenstrauss) are dealing with the question whether every bounded orbit of some natural action on the homogeneous space <math>SL_{2}(\mathbb{R})\backslash SL_{2}(\mathbb{Z})</math> is indeed periodic one, this observation is due to Raghunathan and in different language due to Cassels and Swinnerton-Dyer . Such questions are intimately related to deep measure-classification theorems. | |||
=== Notes === | |||
It is often the case that the evolution function can be understood to compose the elements of a [[group (mathematics)|group]], in which case the [[orbit (group theory)|group-theoretic orbits]] of the [[group action]] are the same thing as the dynamical orbits. | |||
== Examples == | |||
[[File:Critical orbit 3d.png|right|thumb|Critical orbit of discrete dynamical system based on [[complex quadratic polynomial]]. It tends to weakly [[Attractor|attracting]] [[Fixed point (mathematics)|fixed point]] with multiplier=0.99993612384259]] | |||
* The orbit of an [[equilibrium point]] is a constant orbit | |||
== Stability of orbits == | |||
A basic classification of orbits is | |||
* constant orbits or fixed points | |||
* periodic orbits | |||
* non-constant and non-periodic orbits | |||
An orbit can fail to be closed in two ways. | |||
It could be an '''asymptotically periodic''' orbit if it [[limit (mathematics)|converges]] to a periodic orbit. Such orbits are not closed because they never truly repeat, but they become arbitrarily close to a repeating orbit. | |||
An orbit can also be [[chaos theory|chaotic]]. These orbits come arbitrarily close to the initial point, but fail to ever converge to a periodic orbit. They exhibit [[sensitive dependence on initial conditions]], meaning that small differences in the initial value will cause large differences in future points of the orbit. | |||
There are other properties of orbits that allow for different classifications. An orbit can be [[hyperbolic (dynamical systems)|hyperbolic]] if nearby points approach or diverge from the orbit exponentially fast. | |||
==See also== | |||
* [[Wandering set]] | |||
* [[Phase space method]] | |||
* [[Cobweb plot]] or Verhulst diagram | |||
* [[Periodic points of complex quadratic mappings]] and multiplier of orbit | |||
==References== | |||
* {{cite book | author=Anatole Katok and Boris Hasselblatt | title= Introduction to the modern theory of dynamical systems | publisher= Cambridge | year= 1996 | isbn=0-521-57557-5}} | |||
[[Category:Dynamical systems]] | |||
[[Category:Group actions]] | |||
Revision as of 11:22, 29 January 2014
Template:No footnotes In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the phase space. Understanding the properties of orbits by using topological methods is one of the objectives of the modern theory of dynamical systems.
For discrete-time dynamical systems the orbits are sequences, for real dynamical systems the orbits are curves and for holomorphic dynamical systems the orbits are Riemann surfaces.
Definition
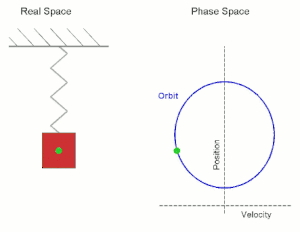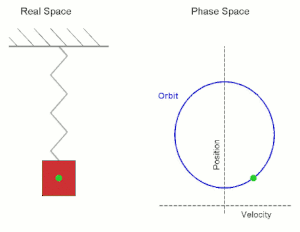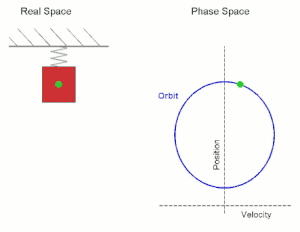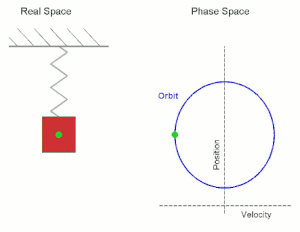
Given a dynamical system (T, M, Φ) with T a group, M a set and Φ the evolution function
we define
then the set
is called orbit through x. An orbit which consists of a single point is called constant orbit. A non-constant orbit is called closed or periodic if there exists a t in T so that
for every point x on the orbit.
Real dynamical system
Given a real dynamical system (R, M, Φ), I(x)) is an open interval in the real numbers, that is . For any x in M
is called positive semi-orbit through x and
is called negative semi-orbit through x.
Discrete time dynamical system
For discrete time dynamical system :
forward orbit of x is a set :
backward orbit of x is a set :
and orbit of x is a set :
where :
- is an evolution function which is here an iterated function,
- set is dynamical space,
- is number of iteration, which is natural number and
- is initial state of system and
Usually different notation is used :
General dynamical system
For general dynamical system, especially in homogeneous dynamics, when one have a "nice" group acting on a probability space in a measure-preserving way, an orbit will be called periodic (or equivalently, closed orbit) if the stabilizer is a lattice inside .
In addition, a related term is bounded orbit, when the set is pre-compact inside .
The classification of orbits can lead to interesting questions with relations to other mathematical areas, for example the Oppenheim conjecture (proved by Margulis) and the Littlewood conjecture (partially proved by Lindenstrauss) are dealing with the question whether every bounded orbit of some natural action on the homogeneous space is indeed periodic one, this observation is due to Raghunathan and in different language due to Cassels and Swinnerton-Dyer . Such questions are intimately related to deep measure-classification theorems.
Notes
It is often the case that the evolution function can be understood to compose the elements of a group, in which case the group-theoretic orbits of the group action are the same thing as the dynamical orbits.
Examples
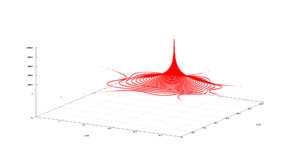
- The orbit of an equilibrium point is a constant orbit
Stability of orbits
A basic classification of orbits is
- constant orbits or fixed points
- periodic orbits
- non-constant and non-periodic orbits
An orbit can fail to be closed in two ways. It could be an asymptotically periodic orbit if it converges to a periodic orbit. Such orbits are not closed because they never truly repeat, but they become arbitrarily close to a repeating orbit. An orbit can also be chaotic. These orbits come arbitrarily close to the initial point, but fail to ever converge to a periodic orbit. They exhibit sensitive dependence on initial conditions, meaning that small differences in the initial value will cause large differences in future points of the orbit.
There are other properties of orbits that allow for different classifications. An orbit can be hyperbolic if nearby points approach or diverge from the orbit exponentially fast.
See also
- Wandering set
- Phase space method
- Cobweb plot or Verhulst diagram
- Periodic points of complex quadratic mappings and multiplier of orbit
References
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534



























