Main Page

In mathematics, the spectrum of a C*-algebra or dual of a C*-algebra A, denoted Â, is the set of unitary equivalence classes of irreducible *-representations of A. A *-representation π of A on a Hilbert space H is irreducible if, and only if, there is no closed subspace K different from H and {0} which is invariant under all operators π(x) with x ∈ A. We implicitly assume that irreducible representation means non-null irreducible representation, thus excluding trivial (i.e. identically 0) representations on one-dimensional spaces. As explained below, the spectrum  is also naturally a topological space; this generalizes the notion of the spectrum of a ring.

One of the most important applications of this concept is to provide a notion of dual object for any locally compact group. This dual object is suitable for formulating a Fourier transform and a Plancherel theorem for unimodular separable locally compact groups of type I and a decomposition theorem for arbitrary representations of separable locally compact groups of type I. The resulting duality theory for locally compact groups is however much weaker than the Tannaka–Krein duality theory for compact topological groups or Pontryagin duality for locally compact abelian groups, both of which are complete invariants. That the dual is not a complete invariant is easily seen as the dual of any finite dimensional full matrix algebra M_n(C) consists of a single point.

Primitive spectrum

The topology of  can be defined in several equivalent ways. We first define it in terms of the primitive spectrum .

The primitive spectrum of A is the set of primitive ideals Prim(A) of A, where a primitive ideal is the kernel of an irreducible *-representation. The set of primitive ideals is a topological space with the hull-kernel topology (or Jacobson topology). This is defined as follows: If X is a set of primitive ideals, its hull-kernel closure is

${\overline {X}}=\{\rho \in \operatorname {Prim} (A):\rho \supseteq \bigcap _{\pi \in X}\pi \}.$

Hull-kernel closure is easily shown to be an idempotent operation, that is

${\overline {\overline {X}}}={\overline {X}},$

and it can be shown to satisfy the Kuratowski closure axioms. As a consequence, it can be shown that there is a unique topology τ on Prim(A) such that the closure of a set X with respect to τ is identical to the hull-kernel closure of X.

Since unitarily equivalent representations have the same kernel, the map π Template:Mapsto ker(π) factors through a surjective map

$\operatorname {k} :{\hat {A}}\rightarrow \operatorname {Prim} (A).$

We use the map k to define the topology on  as follows:

Definition. The open sets of  are inverse images k⁻¹(U) of open subsets U of Prim(A). This is indeed a topology.

The hull-kernel topology is an analogue for non-commutative rings of the Zariski topology for commutative rings.

The topology on  induced from the hull-kernel topology has other characterizations in terms of states of A.

Examples

Commutative C*-algebras

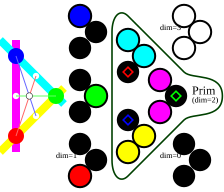
3-dimensional commutative C*-algebra and its ideals. Each of 8 ideals corresponds to a closed subset of discrete 3-points space (or to an open complement). Primitive ideals correspond to closed singletons. See details at the image description page.

The spectrum of a commutative C*-algebra A coincides with the usual dual of A (not to be confused with the dual A' of the Banach space A). In particular, suppose X is a compact Hausdorff space. Then there is a natural homeomorphism

$\operatorname {I} :X\cong \operatorname {Prim} (\operatorname {C} (X)).$

This mapping is defined by

$\operatorname {I} (x)=\{f\in \operatorname {C} (X):f(x)=0\}.$

I(x) is a closed maximal ideal in C(X) so is in fact primitive. For details of the proof, see the Dixmier reference. For a commutative C*-algebra,

${\hat {A}}\cong \operatorname {Prim} (A).$

The C*-algebra of bounded operators

Let H be a separable Hilbert space. L(H) has two norm-closed *-ideals: I₀ = {0} and the ideal K = K(H) of compact operators. Thus as a set, Prim(L(H)) = {I₀, K}. Now

• {K} is a closed subset of Prim(L(H)).

• The closure of {I₀} is Prim(L(H)).

Thus Prim(L(H)) is a non-Hausdorff space.

The spectrum of L(H) on the other hand is much larger. There are many inequivalent irreducible representations with kernel K(H) or with kernel {0}.

Finite dimensional C*-algebras

Suppose A is a finite dimensional C*-algebra. It is known A is isomorphic to a finite direct sum of full matrix algebras:

$A\cong \bigoplus _{e\in \operatorname {min} (A)}Ae,$

where min(A) are the minimal central projections of A. The spectrum of A is canonically isomorphic to min(A) with the discrete topology. For finite dimensional C*-algebras, we also have the isomorphism

${\hat {A}}\cong \operatorname {Prim} (A).$

Other characterizations of the spectrum

The hull-kernel topology is easy to describe abstractly, but in practice for C*-algebras associated to locally compact topological groups, other characterizations of the topology on the spectrum in terms of positive definite functions are desirable.

In fact, the topology on  is intimately connected with the concept of weak containment of representations as is shown by the following:

Theorem. Let S be subset of Â. Then the following are equivalent for an irreducile representation π

1. The equivalence class of π in  is in the closure of S
2. Every state associated to π, that is one of the form

$f_{\xi }(x)=\langle \xi \mid \pi (x)\xi \rangle$

with ||ξ||=1, is the weak limit of states associated to representations in S.

The second condition means exactly that π is weakly contained in S.

The GNS construction is a recipe for associating states of a C*-algebra A to representations of A. By one of the basic theorems associated to the GNS construction, a state f is pure if and only if the associated representation π_f is irreducible. Moreover, the mapping κ: PureState(A) → Â defined by f Template:Mapsto π_f is a surjective map.

From the previous theorem one can easily prove the following;

Theorem The mapping

$\kappa :\operatorname {PureState} (A)\rightarrow {\hat {A}}$

given by the GNS construction is continuous and open.

The space Irr_n(A)

There is yet another characterization of the topology on  which arises by considering the space of representations as a topological space with an appropriate pointwise convergence topology. More precisely, let n be a cardinal number and let H_n be the canonical Hilbert space of dimension n.

Irr_n(A) is the space of irreducible *-representations of A on H_n with the point-weak topology. In terms of convergence of nets, this topology is defined by π_i → π if and only if

$\langle \pi _{i}(x)\xi \mid \eta \rangle \rightarrow \langle \pi (x)\xi \mid \eta \rangle \quad \forall \xi ,\eta \in H_{n}\ x\in A.$

It turns out that this topology on Irr_n(A) is the same as the point-strong topology, i.e. π_i → π if and only if

$\pi _{i}(x)\xi \rightarrow \pi (x)\xi \quad {\mbox{ normwise }}\forall \xi \in H_{n}\ x\in A.$

Theorem. Let Â_n be the subset of  consisting of equivalence classes of representations whose underlying Hilbert space has dimension n. The canonical map Irr_n(A) → Â_n is continuous and open. In particular, Â_n can be regarded as the quotient topological space of Irr_n(A) under unitary equivalence.

Remark. The piecing together of the various Â_n can be quite complicated.

Mackey Borel structure

 is a topological space and thus can also be regarded as a Borel space. A famous conjecture of G. Mackey proposed that a separable locally compact group is of type I if and only if the Borel space is standard, i.e. is isomorphic (in the category of Borel spaces) to the underlying Borel space of a complete separable metric space. Mackey called Borel spaces with this property smooth. This conjecture was proved by James Glimm for separable C*-algebras in the 1961 paper listed in the references below.

Definition. A non-degenerate *-representation π of a separable C*-algebra A is a factor representation if and only if the center of the von Neumann algebra generated by π(A) is one-dimensional. A C*-algebra A is of type I if and only if any separable factor representation of A is a finite or countable multiple of an irreducible one.

Examples of separable locally compact groups G such that C*(G) is of type I are connected (real) nilpotent Lie groups and connected real semi-simple Lie groups. Thus the Heisenberg groups are all of type I. Compact and abelian groups are also of type I.

Theorem. If A is separable, Â is smooth if and only if A is of type I.

The result implies a far-reaching generalization of the structure of representations of separable type I C*-algebras and correspondingly of separable locally compact groups of type I.

Algebraic primitive spectra

Since a C*-algebra A is a ring, we can also consider the set of primitive ideals of A, where A is regarded algebraically. For a ring an ideal is primitive if and only if it is the annihilator of a simple module. It turns out that for a C*-algebra A, an ideal is algebraically primitive if and only if it is primitive in the sense defined above.

Theorem. Let A be a C*-algebra. Any algebraically irreducible representation of A on a complex vector space is algebraically equivalent to a topologically irreducible *-representation on a Hilbert space. Topologically irreducible *-representations on a Hilbert space are algebraically isomorphic if and only if they are unitarily equivalent.

This is the Corollary of Theorem 2.9.5 of the Dixmier reference.

If G is a locally compact group, the topology on dual space of the group C*-algebra C*(G) of G is called the Fell topology, named after J. M. G. Fell.

References

• J. Dixmier, Les C*-algèbres et leurs représentations, Gauthier-Villars, 1969.
• J. Glimm, Type I C*-algebras, Annals of Mathematics, vol 73, 1961.
• G. Mackey, The Theory of Group Representations, The University of Chicago Press, 1955.