Matrix pencil

In statistics, a mediation model is one that seeks to identify and explicate the mechanism or process that underlies an observed relationship between an independent variable and a dependent variable via the inclusion of a third explanatory variable, known as a mediator variable. Rather than hypothesizing a direct causal relationship between the independent variable and the dependent variable, a mediational model hypothesizes that the independent variable influences the mediator variable, which in turn influences the dependent variable. Thus, the mediator variable serves to clarify the nature of the relationship between the independent and dependent variables.[1] In other words, mediating relationships occur when a third variable plays an important role in governing the relationship between the other two variables.
Researchers are now focusing their studies on better understanding known findings. Mediation analyses are employed to understand a known relationship by exploring the underlying mechanism or process by which one variable (X) influences another variable (Y). For example, a cause X of some variable (Y) presumably precedes Y in time and has a generative mechanism that accounts for its impact on Y.[2] Thus, if gender is thought to be the cause of some characteristic, one assumes that other social or biological mechanisms are present in the concept of gender that can explain how gender-associated differences arise. The explicit inclusion of such a mechanism is called a mediator.
Baron and Kenny's (1986) Steps for Mediation
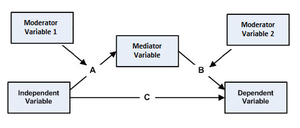
Baron and Kenny (1986) [3] laid out several requirements that must be met to form a true mediation relationship. They are outlined below using a real world example. See the diagram above for a visual representation of the overall mediating relationship to be explained.
Step 1:
- Regress the dependent variable on the independent variable. In other words, confirm that the independent variable is a significant predictor of the dependent variable.
Independent Variable Dependent Variable
- β11 is significant
Step2:
- Regress the mediator on the independent variable. In other words, confirm that the independent variable is a significant predictor of the mediator. If the mediator is not associated with the independent variable, then it couldn’t possibly mediate anything.
- β21 is significant
Step 3:
- Regress the dependent variable on both the mediator and independent variable. In other words, confirm that the mediator is a significant predictor of the dependent variable, while controlling for the independent variable.
This step involves demonstrating that when the mediator and the independent variable are used simultaneously to predict the dependent variable, the previously significant path between the independent and dependent variable (Step #1) is now greatly reduced, if not nonsignificant.
- β32 is significant
- β31 should be smaller in absolute value than the original mediation effect (β11 above)
Example
The following example, drawn from Howell (2009),[4] explains each step of Baron and Kenny’s requirements to understand further how a mediation effect is characterized. Step 1 and step 2 use simple regression analysis, whereas step 3 uses multiple regression analysis.
Step 1:
- How you were parented (i.e., independent variable) predicts how confident you feel about parenting your own children (i.e., dependent variable).
How you were parented Confidence in own parenting abilities.
Step 2:
- How you were parented (i.e., independent variable) predicts your feelings of competence and self-esteem (i.e., mediator).
How you were parented Feelings of competence and self-esteem.
Step 3:
- Your feelings of competence and self-esteem (i.e., mediator) predict how confident you feel about parenting your own children (i.e., dependent variable), while controlling for how you were parented (i.e., independent variable).
Such findings would lead to the conclusion implying that your feelings of competence and self-esteem mediate the relationship between how you were parented and how confident you feel about parenting your own children.
Note: If step 1 does not yield a significant result, one may still have grounds to move to step 2. Sometimes there is actually a significant relationship between independent and dependent variables but because of small sample sizes, or other extraneous factors, there could not be enough power to predict the effect that actually exists (See Shrout & Bolger, 2002 [5] for more info).
Direct Versus Indirect Mediation Effects
In the diagram shown above, the indirect effect is the product of path coefficients "A" and "B". The direct effect is the coefficient "C". The direct effect measures the extent to which the dependent variable changes when the independent variable increases by one unit. In contrast, the indirect effect measures the extent to which the dependent variable changes when the independent variable is held fixed and the mediator variable changes by the amount it would have changed had the independent variable increased by one unit.[6][7] In linear systems, the total effect is equal to the sum of the direct and indirect effects (C + AB in the model above). In nonlinear models, the total effect is not generally equal to the sum of the direct and indirect effects, but to a modified combination of the two.[7]
Full versus partial mediation
A mediator variable can either account for all or some of the observed relationship between two variables.
Full mediation
Maximum evidence for mediation, also called full mediation, would occur if inclusion of the mediation variable drops the relationship between the independent variable and dependent variable (see pathway c in diagram above) to zero. This rarely, if ever, occurs. The most likely event is that c becomes a weaker, yet still significant path with the inclusion of the mediation effect.
Partial mediation
Partial mediation maintains that the mediating variable accounts for some, but not all, of the relationship between the independent variable and dependent variable. Partial mediation implies that there is not only a significant relationship between the mediator and the dependent variable, but also some direct relationship between the independent and dependent variable.
In order for either full or partial mediation to be established, the reduction in variance explained by the independent variable must be significant as determined by one of several tests, such as the Sobel test.[8] The effect of an independent variable on the dependent variable can become nonsignificant when the mediator is introduced simply because a trivial amount of variance is explained (i.e., not true mediation). Thus, it is imperative to show a significant reduction in variance explained by the independent variable before asserting either full or partial mediation. It is possible to have statistically significant indirect effects in the absence of a total effect.[9] This can be explained by the presence of several mediating paths that cancel each other out, and become noticeable when one of the cancelling mediators is controlled for. This implies that the terms 'partial' and 'full' mediation should always be interpreted relative to the set of variables that are present in the model. In all cases, the operation of "fixing a variable" must be distinguished from that of "controlling for a variable," which has been inappropriately used in the literature.[6][10] The former stands for physically fixing, while the latter stands for conditioning on, adjusting for, or adding to the regression model. The two notions coincide only when all error terms (not shown in the diagram) are statistically uncorrelated. When errors are correlated, adjustments must be made to neutralize those correlations before embarking on mediation analysis (see Bayesian Networks).
Sobel's Test
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
As mentioned above, Sobel’s test[8] is calculated to determine if the relationship between the independent variable and dependent variable has been significantly reduced after inclusion of the mediator variable. In other words, this test assesses whether a mediation effect is significant.
Examines the relationship between the independent variable and the dependent variable compared to the relationship between the independent variable and dependent variable including the mediation factor.
The Sobel test is more accurate than the Baron and Kenny steps explained above, however it does have low statistical power. As such, large sample sizes are required in order to have sufficient power to detect significant effects. This is because the key assumption of Sobel’s test is the assumption of normality. Because Sobel’s test evaluates a given sample on the normal distribution, small sample sizes and skewness of the sampling distribution can be problematic (See Normal Distribution for more details). Thus, the general rule of thumb as suggested by MacKinnon et al., (2002) [11] is that a sample size of 1000 is required to detect a small effect, a sample size of 100 is sufficient in detecting a medium effect, and a sample size of 50 is required to detect a large effect.
Preacher & Hayes (2004) Bootstrap Method
The bootstrapping method provides some advantages to the Sobel’s test, primarily an increase in power. The Preacher and Hayes Bootstrapping method is a non-parametric test (See Non-parametric statistics for a discussion on why non parametric tests have more power). As such, the bootstrap method does not violate assumptions of normality and is therefore recommended for small sample sizes. Bootstrapping involves repeatedly randomly sampling observations with replacement from the data set to compute the desired statistic in each resample. Over hundreds, or thousands, of bootstrap resamples provide an approximation of the sampling distribution of the statistic of interest. Hayes offers a macro <http://www.afhayes.com/> that calculates bootstrapping directly within SPSS, a computer program used for statistical analyses. This method provides point estimates and confidence intervals by which one can assess the significance or nonsignificance of a mediation effect. Point estimates reveal the mean over the number of bootstrapped samples and if zero does not fall between the resulting confidence intervals of the bootstrapping method, one can confidently conclude that there is a significant mediation effect to report.
Significance of mediation
As outlined above, there are a few different options one can choose from to evaluate a mediation model.
Bootstrapping[12][13] is becoming the most popular method of testing mediation because it does not require the normality assumption to be met, and because it can be effectively utilized with smaller sample sizes (N<25). However, mediation continues to be most frequently determined using the logic of Baron and Kenny [14] or the Sobel test. It is becoming increasingly more difficult to publish tests of mediation based purely on the Baron and Kenny method or tests that make distributional assumptions such as the Sobel test. Thus, it is important to consider your options when choosing which test to conduct.[9]
Approaches to Mediation
While the concept of mediation as defined within psychology is theoretically appealing, the methods used to study mediation empirically have been challenged by statisticians and epidemiologists[6][10][15] and interpreted formally.[7]
(1) Experimental-Causal-Chain Design
An experimental-causal-chain design is used when the proposed mediator is experimentally manipulated. Such a design implies that one manipulates some controlled third variable that they have reason to believe could be the underlying mechanism of a given relationship.
(2) Measurement-of-Mediation Design
A measurement-of-mediation design can be conceptualized as a statistical approach. Such a design implies that one measures the proposed intervening variable and then uses statistical analyses to establish mediation. This approach does not involve manipulation of the hypothesized mediating variable, but only involves measurement.
See Spencer et al., 2005 [16] for a discussion on the approaches mentioned above.
Criticisms of Mediation Measurement
Experimental approaches to mediation must be carried out with caution. First, it is important to have strong theoretical support for the exploratory investigation of a potential mediating variable. A criticism of a mediation approach rests on the ability to manipulate and measure a mediating variable. Thus, one must be able to manipulate the proposed mediator in an acceptable and ethical fashion. As such, one must be able to measure the intervening process without interfering with the outcome. The mediator must also be able to establish construct validity of manipulation. One of the most common criticisms of the measurement-of-mediation approach is that it is ultimately a correlational design. Consequently, it is possible that some other third variable, independent from the proposed mediator, could be responsible for the proposed effect. However, researchers have worked hard to provide counter evidence to this disparagement. Specifically, the following counter arguments have been put forward:[2]
(1) Temporal precedence. For example, if the independent variable precedes the dependent variable in time, this would provide evidence suggesting a directional, and potentially causal, link from the independent variable to the dependent variable.
(2) Nonspuriousness and/or no confounds. For example, should one identify other third variables and prove that they do not alter the relationship between the independent variable and the dependent variable he/she would have a stronger argument for their mediation effect. See other 3rd variables below.
Mediation can be an extremely useful and powerful statistical test, however it must be used properly. It is important that the measures used to assess the mediator and the dependent variable are theoretically distinct and that the independent variable and mediator cannot interact. Should there be an interaction between the independent variable and the mediator one would have grounds to investigate moderation.
Other Third Variables
(1) Confounding:
- Another model that is often tested is one in which competing variables in the model are alternative potential mediators or an unmeasured cause of the dependent variable. An additional variable in a causal model may obscure or confound the relationship between the independent and dependent variables. Potential confounders are variables that may have a causal impact on both the independent variable and dependent variable. They include common sources of measurement error (as discussed above) as well as other influences shared by both the independent and dependent variables.
In experimental studies, there is a special concern about aspects of the experimental manipulation or setting that may account for study effects, rather than the motivating theoretical factor. Any of these problems may produce spurious relationships between the independent and dependent variables as measured. Ignoring a confounding variable may bias empirical estimates of the causal effect of the independent variable.
(2) Suppression:
- Suppression variables increase the predictive validity of another variable by its inclusion into a regression equation. For example, higher intelligence scores (X) cause a decrease in errors made at work on an assembly line (Y). However an increase in intelligence (X) could cause an increase in errors made on an assembly line (Y) as it may also relate to an increase in boredom while at work (Z) thereby introducing an element of carelessness resulting in a higher percentage of errors made on the job. Such a suppressor variable will lead to an increase in magnitude of the relationship between two variables.
In general, the omission of suppressors or confounders will lead to either an underestimation or an overestimation of the effect of X on Y, thereby either reducing or artificially inflating the magnitude of a relationship between two variables.
(3) Moderators:
- Other important third variables are moderators. Moderators are variables that can make the relationship between two variables either stronger or weaker. Such variables further characterize interactions in regression by affecting the direction and/or strength of the relationship between X and Y. A moderating relationship can be thought of as an interaction. It occurs when the relationship between variables A and B depends on the level of C. See moderation for further discussion.
Mediator Variable
A mediator variable (or mediating variable, or intervening variable) in statistics is a variable that describes how, rather than when, effects will occur by accounting for the relationship between the independent and dependent variables. A mediating relationship is one in which the path relating A to C is mediated by a third variable (B).
For example, a mediating variable explains the actual relationship between the following variables. Most people will agree that older drivers (up to a certain point), are better drivers. Thus:
But what is missing from this relationship is a mediating variable that is actually causing the improvement in driving: experience. The mediated relationship would look like the following:
Mediating variables are often contrasted with moderating variables, which pinpoint the conditions under which an independent variable exerts its effects on a dependent variable.
Moderated Mediation
Mediation and moderation can co-occur in statistical models. It is possible to mediate moderation and moderate mediation.
Moderated mediation is when the effect of the treatment A on the mediator and/or the partial effect B on the dependent variable depend in turn on levels of another variable (moderator). Essentially, in moderated mediation, mediation is first established, and then one investigates if the mediation effect that describes the relationship between the independent variable and dependent variable is moderated by different levels of another variable (i.e., a moderator). This definition has been outlined by Muller, Judd, and Yzerbyt (2005)[17] and Preacher, Rucker, and Hayes (2007).[18]
Models of Moderated Mediation
There are five possible models of moderated mediation, as illustrated in the diagrams below.[17]
- In the first model the independent variable also moderates the relationship between the mediator and the dependent variable.
- The second possible model of moderated mediation involves a new variable which moderates the relationship between the independent variable and the mediator (the A path).
- The third model of moderated mediation involves a new moderator variable which moderates the relationship between the mediator and the dependent variable (the B path).
- Moderated mediation can also occur when one moderating variable affects both the relationship between the independent variable and the mediator (the A path) and the relationship between the mediator and the dependent variable (the B path).
- The fifth and final possible model of moderated mediation involves two new moderator variables, one moderating the A path and the other moderating the B path.
Mediated Moderation
Mediated moderation is a variant of both moderation and mediation. This is where there is initially overall moderation and the direct effect of the moderator variable on the outcome is mediated. The main difference between mediated moderation and moderated mediation is that for the former there is initial (overall) moderation and this effect is mediated and for the latter there is no moderation but the effect of either the treatment on the mediator (path A) is moderated or the effect of the mediator on the outcome (path B) is moderated.[17]
In order to establish mediated moderation, one must first establish moderation, meaning that the direction and/or the strength of the relationship between the independent and dependent variables (path C) differs depending on the level of a third variable (the moderator variable). Researchers next look for the presence of mediated moderation when they have a theoretical reason to believe that there is a fourth variable that acts as the mechanism or process that causes the relationship between the independent variable and the moderator (path A) or between the moderator and the dependent variable (path C).
Example
The following is a published example of mediated moderation in psychological research.[19] Participants were presented with an initial stimulus (a prime) that made them think of morality or made them think of might. They then participated in the Prisoner’s Dilemma Game (PDG), in which participants pretend that they and their partner in crime have been arrested, and they must decide whether to remain loyal to their partner or to compete with their partner and cooperate with the authorities. The researchers found that prosocial individuals were affected by the morality and might primes, whereas proself individuals were not. Thus, social value orientation (proself vs. prosocial) moderated the relationship between the prime (independent variable: morality vs. might) and the behaviour chosen in the PDG (dependent variable: competitive vs. cooperative).
The researchers next looked for the presence of a mediated moderation effect. Regression analyses revealed that the type of prime (morality vs. might) mediated the moderating relationship of participants’ social value orientation on PDG behaviour. Prosocial participants who experienced the morality prime expected their partner to cooperate with them, so they chose to cooperate themselves. Prosocial participants who experienced the might prime expected their partner to compete with them, which made them more likely to compete with their partner and cooperate with the authorities. In contrast, participants with a pro-self social value orientation always acted competitively.
Regression Equations for Moderated Mediation and Mediated Moderation
Muller, Judd, and Yzerbyt (2005)[17] outline three fundamental models that underlie both moderated mediation and mediated moderation. Mo represents the moderator variable(s), Me represents the mediator variable(s), and εi represents the measurement error of each regression equation.

Step 1: Moderation of the relationship between the independent variable (X) and the dependent variable (Y), also called the overall treatment effect (path C in the diagram).
- To establish overall moderation, the β43 regression weight must be significant (first step for establishing mediated moderation).
- Establishing moderated mediation requires that there be no moderation effect, so the β43 regression weight must not be significant.
Step 2: Moderation of the relationship between the independent variable and the mediator (path A).
- If the β53 regression weight is significant, the moderator affects the relationship between the independent variable and the mediator.
Step 3: Moderation of both the relationship between the independent and dependent variables (path A) and the relationship between the mediator and the dependent variable (path B).
- If both β53 in step 2 and β63 in step 3 are significant, the moderator affects the relationship between the independent variable and the mediator (path A).
- If both β53 in step 2 and β65 in step 3 are significant, the moderator affects the relationship between the mediator and the dependent variable (path B).
- Either or both of the conditions above may be true.
References
- Notes
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
- Bibliography
- One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - Baron, R. M. and Kenny, D. A. (1986) "The Moderator-Mediator Variable Distinction in Social Psychological Research – Conceptual, Strategic, and Statistical Considerations", Journal of Personality and Social Psychology, Vol. 51(6), pp. 1173–1182.
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). New York, NY: Academic Press.
- One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - Howell, D. C. (2009). Statistical methods for psychology (7th ed.). Belmot, CA: Cengage Learning.
- One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - Rucker, D.D., Preacher, K.J., Tormala, Z.L. & Petty, R.E. (2011). "Mediation analysis in social psychology: Current practices and new recommendations". Social and Personality Psychology Compass, 5/6, 359-371.
- One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
External links
- Summary of mediation methods at PsychWiki
- Example of Causal Mediation Using Propensity Scores The Methodology Center, Penn State University
- Book on moderation and mediation analysis, including an introduction to the PROCESS macro for SPSS and SAS Andrew F. Hayes, Ohio State University
- ↑ MacKinnon, D. P. (2008). Introduction to Statistical Mediation Analysis. New York: Erlbaum.
- ↑ 2.0 2.1 Cohen, J.; Cohen, P.; West, S. G.; Aiken, L. S. (2003) Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah, NJ: Erlbaum.
- ↑ Baron, R. M. and Kenny, D. A. (1986) "The Moderator-Mediator Variable Distinction in Social Psychological Research – Conceptual, Strategic, and Statistical Considerations", Journal of Personality and Social Psychology, Vol. 51(6), pp. 1173–1182.
- ↑ Howell, D. C. (2009). Statistical methods for psychology (7th ed.). Belmot, CA: Cengage Learning.
- ↑ Shrout, P. E., & Bolger, N. (2002). Mediation in experimental and nonexperimental studies: New procedures and recommendations. Psychological Methods, 7(4), 422-445
- ↑ 6.0 6.1 6.2 One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ 7.0 7.1 7.2 Pearl, J. (2001) "Direct and indirect effects". Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence, Morgan Kaufmann, 411–420.
- ↑ 8.0 8.1 One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ 9.0 9.1 One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ 10.0 10.1 Kaufman, J. S., MacLehose R. F., Kaufman S (2004). A further critique of the analytic strategy of adjusting for covariates to identify biologic mediation. Epidemiology Innovations and Perspectives, 1:4.
- ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ "Mediation". davidakenny.net. Retrieved April 25, 2012.
- ↑ Bullock, J. G., Green, D. P., Ha, S. E. (2010). Yes, but what's the mechanism? (Don't expect an easy answer). Journal of Personality & Social Psychology, 98(4):550-558.
- ↑ Spencer, S. J., Zanna, M. P., & Fong, G. T. (2005). Establishing a causal chain: why experiments are often more effective than meditational analyses in examining psychological processes. Attitudes and Social Cognition, 89(6): 845-851.
- ↑ 17.0 17.1 17.2 17.3 One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ Preacher, K. J., Rucker, D. D. & Hayes, A. F. (2007). Assessing moderated mediation hypotheses: Strategies, methods, and prescriptions. Multivariate Behavioral Research, 42, 185–227.
- ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang