Riemann's differential equation: Difference between revisions
improve |
en>Incnis Mrsi m →Definition: "texhtml" compatibility tweak: see template talk:Mvar. not to say I agree with user:Edokter, but I do not see enough merit to continue the flamewar |
||
| Line 1: | Line 1: | ||
[[File:Minimal surface curvature planes-en.svg|thumb|300px|right|[[Saddle surface]] with normal planes in directions of principal curvatures]] | |||
In [[differential geometry]], the two '''principal curvatures''' at a given point of a [[surface]] are the [[eigenvalues]] of the [[shape operator]] at the point. They measure how the surface bends by different amounts in different directions at that point. | |||
==Discussion== | |||
At each point ''p'' of a [[differentiable manifold|differentiable]] [[surface]] in 3-dimensional [[Euclidean space]] one may choose a unit normal vector. A normal plane at ''p'' is one that contains the normal, and will therefore also contain a unique direction tangent to the surface and cut the surface in a plane curve. This curve will in general have different [[curvature]]s for different normal planes at ''p''. The '''principal curvatures''' at ''p'', denoted ''k''<sub>1</sub> and ''k''<sub>2</sub>, are the maximum and minimum values of this curvature. | |||
Here the curvature of a curve is by definition the [[multiplicative inverse|reciprocal]] of the [[radius]] of the [[osculating circle]]. The curvature is taken to be positive if the curve turns in the same direction as the surface's chosen normal, and otherwise negative. The directions of the normal plane where the curvature takes its maximum and minimum values are always perpendicular, if ''k''<sub>1</sub> does not equal ''k''<sub>2</sub>, a result of [[Leonhard Euler|Euler]] (1760), and are called '''principal directions'''. From a modern perspective, this theorem follows from the [[spectral theorem]] because these directions are as the [[principal axis theorem|principal axes]] of a [[symmetric tensor]]—the [[second fundamental form]]. A systematic analysis of the principal curvatures and principal directions was undertaken by [[Gaston Darboux]], using [[Darboux frame]]s. | |||
The product ''k''<sub>1</sub>''k''<sub>2</sub> of the two principal curvatures is the [[Gaussian curvature]], ''K'', and the average (''k''<sub>1</sub> + ''k''<sub>2</sub>)/2 is the [[mean curvature]], ''H''. | |||
If at least one of the principal curvatures is zero at every point, then the [[Gaussian curvature]] will be 0 and the surface is a [[developable surface]]. For a [[minimal surface]], the mean curvature is zero at every point. | |||
==Formal definition== | |||
Let ''M'' be a surface in Euclidean space with [[second fundamental form]] <math>I\!I(X,Y)</math>. Fix a point ''p''∈''M'', and an [[orthonormal basis]] ''X''<sub>1</sub>, ''X''<sub>2</sub> of tangent vectors at ''p''. Then the principal curvatures are the eigenvalues of the symmetric matrix | |||
:<math>\left[I\!I_{ij}\right] = | |||
\begin{bmatrix} | |||
I\!I(X_1,X_1)&I\!I(X_1,X_2)\\ | |||
I\!I(X_2,X_1)&I\!I(X_2,X_2) | |||
\end{bmatrix}.</math> | |||
If ''X''<sub>1</sub> and ''X''<sub>2</sub> are selected so that the matrix <math>\left[I\!I_{ij}\right]</math> is a diagonal matrix, then they are called the '''principal directions'''. If the surface is [[orientation (mathematics)|oriented]], then one often requires that the pair (''X''<sub>1</sub>, ''X''<sub>2</sub>) to be positively oriented with respect to the given orientation. | |||
Without reference to a particular orthonormal basis, the principal curvatures are the [[eigenvalue]]s of the [[shape operator]], and the principal directions are its [[eigenvector]]s. | |||
=== Generalizations === | |||
For hypersurfaces in higher dimensional Euclidean spaces, the principal curvatures may be defined in a directly analogous fashion. The principal curvatures are the eigenvalues of the matrix of the second fundamental form <math>I\!I(X_i,X_j)</math> in an orthonormal basis of the tangent space. The principal directions are the corresponding eigenvectors. | |||
Similarly, if ''M'' is a hypersurface in a [[Riemannian manifold]] ''N'', then the principal curvatures are the eigenvalues of its second-fundamental form. If ''k''<sub>1</sub>, ..., ''k''<sub>n</sub> are the ''n'' principal curvatures at a point ''p'' ∈ ''M'' and ''X''<sub>1</sub>, ..., ''X''<sub>''n''</sub> are corresponding orthonormal eigenvectors (principal directions), then the [[sectional curvature]] of ''M'' at ''p'' is given by | |||
:<math>K(X_i,X_j) = k_ik_j.</math> | |||
==Classification of points on a surface== | |||
*At '''elliptical''' points, both principal curvatures have the same sign, and the surface is locally convex. | |||
**At '''[[umbilical point|umbilic points]]''', both principal curvatures are equal and every tangent vector can be considered a principal direction. These typically occur in isolated points. | |||
*At '''hyperbolic''' points, the principal curvatures have opposite signs, and the surface will be locally saddle shaped. | |||
*At '''parabolic''' points, one of the principal curvatures is zero. Parabolic points generally lie in a curve separating elliptical and hyperbolic regions. | |||
** At '''flat umbilic''' points both principal curvatures are zero. A generic surface will not contain flat umbilic points. The [[monkey saddle]] is one surface with an isolated flat umbilic. | |||
==Line of curvature== | |||
The '''lines of curvature''' or '''curvature lines''' are curves which are always tangent to a principal direction (they are [[integral curve]]s for the principal direction fields). There will be two lines of curvature through each non-umbilic point and the lines will cross at right angles. | |||
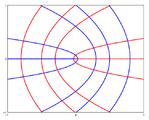
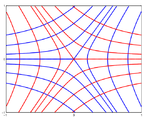
In the vicinity of an umbilic the lines of curvature typically form one of three configurations '''star''', '''lemon''' and '''monstar''' (derived from ''lemon-star'').<ref>Berry, M V, & Hannay, J H, 'Umbilic points on Gaussian random surfaces', J.Phys.A 10, 1977, 1809–21, .</ref> These points are also called Darbouxian Umbilics, in honor to | |||
[[Gaston Darboux]], the first to make a systematic study in Vol. 4, p 455, of his Leçons (1896). | |||
<gallery Caption="configurations of lines of curvature near umbilics" widths="150px"> | |||
Image:TensorLemon.png|Lemon | |||
Image:TensorMonstar.png|Monstar | |||
Image:TensorStar.png|Star | |||
</gallery> | |||
In these figures, the red curves are the lines of curvature for one family of principal directions, and the blue curves for the other. | |||
When a line of curvature has a local extremum of the same principal curvature then the curve has a '''[[ridge (differential geometry)|ridge point]]'''. These ridge points form curves on the surface called '''ridges'''. The ridge curves pass through the | |||
umbilics. For the star pattern either 3 or 1 ridge line pass through the umbilic, for the monstar and lemon only one ridge passes through.<ref>{{Cite book|last=Porteous|first=I. R.|title=Geometric Differentiation|publisher=Cambridge University Press|year=1994|isbn=0-521-39063-X|postscript=<!--None-->}}</ref> | |||
==References== | |||
* {{cite book|first=Gaston|last=Darboux|year=1887,1889,1896|title=Leçons sur la théorie génerale des surfaces: [http://www.hti.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ABV4153.0001.001 Volume I], [http://www.hti.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ABV4153.0002.001 Volume II], [http://www.hti.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ABV4153.0003.001 Volume III], [http://www.hti.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ABV4153.0004.001 Volume IV] | |||
|publisher=Gauthier-Villars}} | |||
* {{cite book|first=Heinrich|last=Guggenheimer|title=Differential Geometry|year=1977|publisher=Dover|chapter=Chapter 10. Surfaces|isbn=0-486-63433-7}} | |||
*{{cite book | author=Kobayashi, Shoshichi and Nomizu, Katsumi | title = Foundations of Differential Geometry, Vol. 2 | publisher=Wiley-Interscience | year=1996 (New edition) |isbn = 0-471-15732-5}} | |||
* {{cite book|last=Spivak|first=Michael|authorlink=Michael Spivak|title=A Comprehensive introduction to differential geometry (Volume 3)|year=1999|publisher=Publish or Perish|isbn=0-914098-72-1}} | |||
<references/> | |||
==External links== | |||
*[http://front.math.ucdavis.edu/0411.5403 Historical Comments on Monge's Ellipsoid and the Configuration of Lines of Curvature on Surfaces Immersed in '''R'''<sup>3</sup>] | |||
{{curvature}} | |||
[[Category:Curvature (mathematics)]] | |||
[[Category:Differential geometry of surfaces]] | |||
[[Category:Surfaces]] | |||
Revision as of 09:19, 12 November 2013

In differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.
Discussion
At each point p of a differentiable surface in 3-dimensional Euclidean space one may choose a unit normal vector. A normal plane at p is one that contains the normal, and will therefore also contain a unique direction tangent to the surface and cut the surface in a plane curve. This curve will in general have different curvatures for different normal planes at p. The principal curvatures at p, denoted k1 and k2, are the maximum and minimum values of this curvature.
Here the curvature of a curve is by definition the reciprocal of the radius of the osculating circle. The curvature is taken to be positive if the curve turns in the same direction as the surface's chosen normal, and otherwise negative. The directions of the normal plane where the curvature takes its maximum and minimum values are always perpendicular, if k1 does not equal k2, a result of Euler (1760), and are called principal directions. From a modern perspective, this theorem follows from the spectral theorem because these directions are as the principal axes of a symmetric tensor—the second fundamental form. A systematic analysis of the principal curvatures and principal directions was undertaken by Gaston Darboux, using Darboux frames.
The product k1k2 of the two principal curvatures is the Gaussian curvature, K, and the average (k1 + k2)/2 is the mean curvature, H.
If at least one of the principal curvatures is zero at every point, then the Gaussian curvature will be 0 and the surface is a developable surface. For a minimal surface, the mean curvature is zero at every point.
Formal definition
Let M be a surface in Euclidean space with second fundamental form . Fix a point p∈M, and an orthonormal basis X1, X2 of tangent vectors at p. Then the principal curvatures are the eigenvalues of the symmetric matrix
If X1 and X2 are selected so that the matrix is a diagonal matrix, then they are called the principal directions. If the surface is oriented, then one often requires that the pair (X1, X2) to be positively oriented with respect to the given orientation.
Without reference to a particular orthonormal basis, the principal curvatures are the eigenvalues of the shape operator, and the principal directions are its eigenvectors.
Generalizations
For hypersurfaces in higher dimensional Euclidean spaces, the principal curvatures may be defined in a directly analogous fashion. The principal curvatures are the eigenvalues of the matrix of the second fundamental form in an orthonormal basis of the tangent space. The principal directions are the corresponding eigenvectors.
Similarly, if M is a hypersurface in a Riemannian manifold N, then the principal curvatures are the eigenvalues of its second-fundamental form. If k1, ..., kn are the n principal curvatures at a point p ∈ M and X1, ..., Xn are corresponding orthonormal eigenvectors (principal directions), then the sectional curvature of M at p is given by
Classification of points on a surface
- At elliptical points, both principal curvatures have the same sign, and the surface is locally convex.
- At umbilic points, both principal curvatures are equal and every tangent vector can be considered a principal direction. These typically occur in isolated points.
- At hyperbolic points, the principal curvatures have opposite signs, and the surface will be locally saddle shaped.
- At parabolic points, one of the principal curvatures is zero. Parabolic points generally lie in a curve separating elliptical and hyperbolic regions.
- At flat umbilic points both principal curvatures are zero. A generic surface will not contain flat umbilic points. The monkey saddle is one surface with an isolated flat umbilic.
Line of curvature
The lines of curvature or curvature lines are curves which are always tangent to a principal direction (they are integral curves for the principal direction fields). There will be two lines of curvature through each non-umbilic point and the lines will cross at right angles.
In the vicinity of an umbilic the lines of curvature typically form one of three configurations star, lemon and monstar (derived from lemon-star).[1] These points are also called Darbouxian Umbilics, in honor to Gaston Darboux, the first to make a systematic study in Vol. 4, p 455, of his Leçons (1896).
- configurations of lines of curvature near umbilics
-
Lemon
-
Monstar
-
Star
In these figures, the red curves are the lines of curvature for one family of principal directions, and the blue curves for the other.
When a line of curvature has a local extremum of the same principal curvature then the curve has a ridge point. These ridge points form curves on the surface called ridges. The ridge curves pass through the umbilics. For the star pattern either 3 or 1 ridge line pass through the umbilic, for the monstar and lemon only one ridge passes through.[2]
References
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
- ↑ Berry, M V, & Hannay, J H, 'Umbilic points on Gaussian random surfaces', J.Phys.A 10, 1977, 1809–21, .
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534

![{\displaystyle \left[I\!I_{ij}\right]={\begin{bmatrix}I\!I(X_{1},X_{1})&I\!I(X_{1},X_{2})\\I\!I(X_{2},X_{1})&I\!I(X_{2},X_{2})\end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bffd43b323463adccee7129a8191ca0ad70344b)
![{\displaystyle \left[I\!I_{ij}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c25a532dc99d4e755b582b3e013b0c91c449144)