Standardized moment
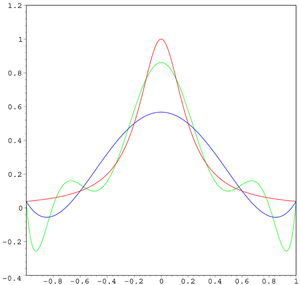
The blue curve is Not solely are individuals shopping for second houses all around the globe but they are also moving to nations which might be sunnier. Singapore is among the international locations where many individuals relocate to and it is due to this that there was an increase in the demand for Singapore property agent. So who's a Singapore property agent?
15.1.1 The law of company plays an vital function in business transactions, notably with the arrival of the fashionable firm which, by a authorized fiction, is considered having character and will enter into transactions in its personal proper. Even with people, it is going to usually be simpler to transact by means of intermediaries. Accordingly, swachhbharatabhiyan.net much each day commercial transacting is facilitated by intermediaries appearing within the scope of the authority that has been conferred on them whether expressly or by implication. By this, the regulation of company is ready to multiply the individual´s authorized personality in area.
Home is where the center is, and choosing the proper house is part of ensuring a cheerful expertise in Singapore. Most expats join a two-year lease with the choice to resume, so it is value taking the time to choose a neighbourhood that has the amenities you want. The specialists at Expat Realtor have compiled the next information to help you negotiate your means by the property minefield. paperless submission of Sale or Rental transactions PIC Grants Singapore Offer Money Bonus s$15000 & Money payout 60% on your buy ! Properties for the aesthete. Boutique actual estate agency for architecturally distinguished, unique properties for hire and for sale. Caters to the niche market of design-savvy individuals. Property agents. Providers for expats.
Step one towards conducting enterprise as an actual estate agency in Singapore is to include a company, or in case you're going the partnership or sole-proprietorship route, register your Limited Legal responsibility Partnership or sole-proprietorship with the ACRA (Accounting and Company Regulatory Authority of Singapore) Whether you're considering to sell, let, lease or buy a new industrial property, we are here to help. Search and browse our commercial property section. Possess at least three years of working expertise under a Singapore licensed actual-property agency; Sale, letting and property administration and taxation providers. three Shenton Approach, #10-08 Shenton Home, Singapore 068805. Actual property brokers for buying, selling, leasing, and renting property. Caveat Search
The Register of Foreign Patent Brokers incorporates particulars of names, follow addresses, dates of their registration, terms of their international patent agent certificates issued, and electronic mail addresses of all overseas patent agents duly registered with the Registrar, Mental Property Workplace of Singapore (IPOS). Neither should an agent do so even if he had helped the individual market a property previously. Particular person and corporate relocations for rental properties. 314 Tanglin Rd, Block F #01-01/02, Phoenix Park Office Campus, Singapore 247977. Paterson Suites in Singapore - Visually beautiful architecture, iconic function in Singapore's panorama. Luxury condominium development offering you the perfect in location, area, privacy and amenities. Featured Agent
There isn't any regulation on the amount of commission. Commission is just payable upon complete switch of the property. If for any reason the deal falls by way of, then he receives nothing from the vendor (vendor) or the owner (owner). He has no right to recuperate whatever expenditure he has incurred in trying to deliver a couple of sale or tenancy. He takes the enterprise threat of dropping his expenses and time when his suggestion will not be accepted by the seller or the owner. Agents must all the time use their company's official settlement.
Many homeowners choose an actual estate agent who tells them the very best value, or one who charged the bottom commission. Avoid an agent who promise you that your home can fetch greater than the market worth. That agent just desires your corporation. You will find yourself not with the ability to sell your own home for a couple of months, then the agent will persuade you to lower your asking value. His suggestion? Cash out and use a part of the income as downpayment for a brand new home. Make investments the remainder in another property to gather lease. Patrons can borrow up to eighty per cent of the price of their first non-public residential property, and 60 per cent for the second. Kelvin points out that there is no such cap for commercial properties as long as you meet the bank's loan criteria. (using six equally-spaced interpolating points).
The green curve is Many property brokers wish to declare for the PIC grant in Singapore. However, not all of them know how to do the proper process for getting this PIC scheme from the IRAS. There are a number of steps that it's a must to do earlier than your utility can be authorized.
By the way in which, there is additionally no real regulatory physique to display screen out inexperienced agents here. As an illustration, when I requested my very own agent what paperwork I would wish to use for loan, she couldn't inform me, she may only advocate a banker I may consult with. But that's like basic data actual estate brokers should know and have the ability to advise their purchasers. That's after we form of lost confidence in property brokers in Singapore overall and their ability to get us an excellent rental in a superb worth too. And we've encounter quite just a few incompetent agents in latest past months.
Why did you join the actual property line, and what do you like most about it? What have you achieved to this point in your real property profession? What is one thing about your real property journey that might shock or amaze individuals? What is a Misrepresentation, the different types of Misrepresentations and how you can avoid from making one? An motion for misrepresentation arises below the legislation of tort. A Misrepresentation occurs when the Representor (Property Agent) makes a false statement of current truth with information of its falsity and with the intention that the Representee (Buyer or Seller) should act on it with the end result that the Representee does act on it to his detriment. It most likely ranks as the lamest cause to enter the real property line. Ever.
Whether you are an skilled investor, a primary- time purchaser or a foreigner seeking to relocate to Singapore, I'll do my best that can assist you find the property you want and want. I'll assist and information you through all the means of your own home search, from property hunting, negotiation for the best price, making a suggestion, to closing the deal. Competitors within the industry is fierce and being extremely pushed and eloquent people, brokers might typically put forth representations to their clients that may, to a sure extent, affect them to enter right into a sale and purchase settlement upon their reliance on such statements being made by the property agents. The aged are simple targets who may be coaxed into selling and shopping for their property.
Read your contracts carefully. In virtually all cases, brokers would have sneakily included a clause in the contract to have the landlord pay them commission once more if the lease is prolonged, even when the agent was not present on the extension of the lease. They might positively let you know that is is legally binding; afterall the contract has been legally stamped. In case you are stuck in such a situation and feel that a fee for the agent is totally unwarranted for, we may also help you out. Drop us an e-mail on the contact web page.
Service Choose Agency and brokerage Hospitality and leisure Industrial and logistics company Investment agency Land company Lease advisory and dispute resolution Workplace agency Residential agency Retail company Consulting Company real property consulting Improvement consulting Hospitality and leisure Planning Retail development consulting Sustainability Funding and asset administration Asset administration Company finance Investment agency Funding administration Occupier companies Project management and constructing consultancy Building consultancy Project management Property and services management Company actual estate administration Facilities management Property management Retail administration Research Valuations and advisory providers Corporate restoration and restructuring http://Streetprayer.org/ Lease advisory and dispute decision Rating and statutory valuations Valuations Search Now.
She is the star in the highly competitive property agency enterprise." GLOBAL PROPERTY STRATEGIC ALLIANCE PTE LTD is accredited by the Council of Estate Brokers underneath the Ministry of Nationwide Growth. The Graduate Certificates in Intellectual Property Regulation programme (GCIP) is a complete foundation IP law course which provides the fundamental IP information that's wanted by aspiring IP professionals and practitioners for a profession within the discipline of Intellectual Property. GPS was founded by Dennis Yong and Jeffrey Hong, both of whom are icons of the present day real property business. Giants in their very own rights, their perception and views on the native property scene are nonetheless highly valued and wanted. Choose and register for the course on a modular foundation (using ten equally-spaced interpolating points).
At the interpolating points, the error between the function and the interpolating polynomial is (by definition) zero. Between the interpolating points (especially in the region close to the endpoints 1 and −1), the error between the function and the interpolating polynomial gets worse for higher-order polynomials.
In the mathematical field of numerical analysis, Runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree over a set of equispaced interpolation points. It was discovered by Carl David Tolmé Runge when exploring the behavior of errors when using polynomial interpolation to approximate certain functions.[1] The discovery was important because it shows that going to higher degrees does not always improve accuracy. The phenomenon is similar to the Gibbs phenomenon in Fourier series approximations.
Introduction
The Weierstrass approximation theorem states that every continuous function f(x) defined on an interval [a,b] can be uniformly approximated as closely as desired by a polynomial function Pn(x) of sufficiently large degree ≤ n, i.e.,
Interpolation at equidistant points is a natural and well-known approach to construct approximating polynomials. Runge's phenomenon demonstrates, however, that interpolation can easily result in divergent approximations.
Problem
Consider the function:
Runge found that if this function is interpolated at equidistant points xi between −1 and 1 such that:
with a polynomial Pn(x) of degree ≤ n, the resulting interpolation oscillates toward the end of the interval, i.e. close to −1 and 1. It can even be proven that the interpolation error increases (without bound) when the degree of the polynomial is increased:
This shows that high-degree polynomial interpolation at equidistant points can be troublesome.
Reason
The error between the generating function and the interpolating polynomial of order n is given by
For the case of the Runge function, interpolated at equidistant points, each of the two multipliers in the upper bound for the approximation error grows to infinity with n. Although often used to explain the Runge phenomenon, the fact that the upper bound of the error goes to infinity does not necessarily imply, of course, that the error itself also diverges with n.
Mitigations to the problem
Change of interpolation points
The oscillation can be minimized by using nodes that are distributed more densely towards the edges of the interval, specifically, with asymptotic density (on the interval [−1,1]) given by the formula[2] . A standard example of such a set of nodes is Chebyshev nodes, for which the maximum error in approximating the Runge function is guaranteed to diminish with increasing polynomial order. The phenomenon demonstrates that high degree polynomials are generally unsuitable for interpolation with equidistant nodes.
Use of piecewise polynomials
The problem can be avoided by using spline curves which are piecewise polynomials. When trying to decrease the interpolation error one can increase the number of polynomial pieces which are used to construct the spline instead of increasing the degree of the polynomials used.
Constrained minimization
One can also fit a polynomial of higher degree (for instance instead of ), and fit an interpolating polynomial whose first (or second) derivative has minimal norm.
Least squares fitting
Another method is fitting a polynomial of lower degree using the method of least squares. Generally, when using m equidistant points, if then least squares approximation is well-conditioned.[3]
Related statements from the approximation theory
For every predefined table of interpolation nodes there is a continuous function for which the interpolation process on those nodes diverges. For every continuous function there is a table of nodes on which the interpolation process converges. Chebyshev interpolation (i.e., on Chebyshev nodes) converges uniformly for every absolutely continuous function.
See also
- Compare with the Gibbs phenomenon for sinusoidal basis functions
- Taylor series
- Chebyshev nodes
- Stone–Weierstrass theorem
References
- ↑ Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 available at www.archive.org - ↑ Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - ↑ Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010












