De Laval nozzle: Difference between revisions
en>Shim'on |
en>BattyBot m fixed CS1 errors: dates & General fixes using AWB (9832) |
||
| Line 1: | Line 1: | ||
[[File:Limit cycle Poincare map.svg|thumb|250px|right|Stable limit cycle (shown in bold) and two other trajectories spiraling into it]] | |||
[[Image:VanDerPolPhaseSpace.png|right|250px|thumb|Stable limit cycle (shown in bold) for the [[Van der Pol oscillator]]]] | |||
In [[mathematics]], in the study of [[dynamical systems]] with two-dimensional [[phase space]], a '''limit cycle''' is a closed [[trajectory]] in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such behavior is exhibited in some [[nonlinear systems]]. The study of limit cycles was initiated by [[Henri Poincaré]] (1854-1912). | |||
==Definition== | |||
We consider a two-dimensional dynamical system of the form | |||
:<math>x'(t)=V(x(t))</math> | |||
where | |||
:<math>V:\mathbb{R}^2\to\mathbb{R}^2</math> | |||
is a smooth function. A ''trajectory'' of this system is some smooth function <math>x(t)</math> with values in <math>\mathbb{R}^2</math> which satisfies this differential equation. Such a trajectory is called ''closed'' (or ''periodic'') if it is not constant but returns to its starting point, i.e. if there exists some <math>t_0>0</math> such that <math>x(t+t_0)=x(t)</math> for all <math>t\in\mathbb{R}</math>. An [[orbit (dynamics)|orbit]] is the [[image (mathematics)|image]] of a trajectory, a subset of <math>\mathbb{R}^2</math>. A ''closed orbit'', or ''cycle'', is the image of a closed trajectory. A ''limit cycle'' is a cycle which is the [[limit set]] of some other trajectory. | |||
==Properties== | |||
By the [[Jordan curve theorem]], every closed trajectory divides the plane into two regions, the interior and the exterior of the curve. | |||
Given a limit cycle and a trajectory in its interior that approaches the limit cycle for time approaching +infinity, then there is a neighborhood around the limit cycle such that ''all'' trajectories in the interior that start in the neighborhood approach the limit cycle for time approaching +infinity. The corresponding statement holds for a trajectory in the interior that approaches the limit cycle for time approaching -infinity, and also for trajectories in the exterior approaching the limit cycle. | |||
==Stable, unstable and semi-stable limit cycles== | |||
In the case where all the neighbouring trajectories approach the limit cycle as time approaches infinity, it is called a ''[[stable manifold|stable]]'' or ''attractive'' limit cycle (ω-limit cycle). If instead all neighbouring trajectories approach it as time approaches negative infinity, then it is an ''unstable'' limit cycle (α-limit cycle). If there is a neighbouring tractory which spirals into the limit cycle as time approaches infinity, and another one which spirals into it as time approaches negative infinity, then it is a ''semi-stable'' limit cycle. There are also limit cycles which are neither stable, unstable nor semi-stable: for instance, a neighboring trajectory may approach the limit cycle from the outside, but the inside of the limit cycle is approached by a family of other cycles (which wouldn't be limit cycles). | |||
Stable limit cycles are examples of [[attractor]]s. They imply self-sustained [[oscillations]]: the closed trajectory describes perfect periodic behavior of the system, and any small perturbation from this closed trajectory causes the system to return to it, making the system stick to the limit cycle. | |||
==Finding limit cycles== | |||
Every closed trajectory contains within its interior a [[stationary point]] of the system, i.e. a point <math>p</math> where <math>V(p)=0</math>. The [[Bendixson–Dulac theorem]] and the [[Poincaré–Bendixson theorem]] predict the absence or existence, respectively, of limit cycles of two-dimensional nonlinear dynamical systems. | |||
==Open problems== | |||
Finding limit cycles in general is a very difficult problem. The number of limit cycles of a polynomial differential equation in the plane is the main object of the second part of [[Hilbert's sixteenth problem]]. It is unknown, for instance, whether there is any system <math>x'=V(x)</math> in the plane where both components of <math>V</math> are quadratic polynomials of the two variables, such that the system has more than 4 limit cycles. | |||
==See also== | |||
* [[Periodic point]] | |||
* [[Stable manifold]] | |||
* [[Hyperbolic set]] | |||
==References== | |||
* {{planetmath reference|id=6722|title=limit cycle}} | |||
* Steven H. Strogatz, "Nonlinear Dynamics and Chaos", Addison Wesley publishing company, 1994. | |||
* M. Vidyasagar, "Nonlinear Systems Analysis, second edition, Prentice Hall, Englewood Cliffs, New Jersey 07632. | |||
* Philip Hartman, "Ordinary Differential Equation", Society for Industrial and Applied Mathematics, 2002. | |||
* Witold Hurewicz, "Lectures on Ordinary Differential Equations", Dover, 2002. | |||
* Solomon Lefschetz, "Differential Equations: Geometric Theory", Dover, 2005. | |||
* Lawrence Perko, "Differential Equations and Dynamical Systems", Springer-Verlag, 2006. | |||
* Arthur Mattuck, Limit Cycles: Existence and Non-existence Criteria, MIT Open Courseware http://videolectures.net/mit1803s06_mattuck_lec32/# | |||
[[Category:Limit sets]] | |||
[[Category:Nonlinear systems]] | |||
[[Category:Dynamical systems]] | |||
Revision as of 08:58, 5 January 2014

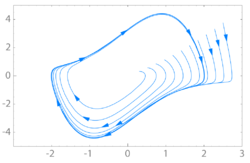
In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such behavior is exhibited in some nonlinear systems. The study of limit cycles was initiated by Henri Poincaré (1854-1912).
Definition
We consider a two-dimensional dynamical system of the form
where
is a smooth function. A trajectory of this system is some smooth function with values in which satisfies this differential equation. Such a trajectory is called closed (or periodic) if it is not constant but returns to its starting point, i.e. if there exists some such that for all . An orbit is the image of a trajectory, a subset of . A closed orbit, or cycle, is the image of a closed trajectory. A limit cycle is a cycle which is the limit set of some other trajectory.
Properties
By the Jordan curve theorem, every closed trajectory divides the plane into two regions, the interior and the exterior of the curve.
Given a limit cycle and a trajectory in its interior that approaches the limit cycle for time approaching +infinity, then there is a neighborhood around the limit cycle such that all trajectories in the interior that start in the neighborhood approach the limit cycle for time approaching +infinity. The corresponding statement holds for a trajectory in the interior that approaches the limit cycle for time approaching -infinity, and also for trajectories in the exterior approaching the limit cycle.
Stable, unstable and semi-stable limit cycles
In the case where all the neighbouring trajectories approach the limit cycle as time approaches infinity, it is called a stable or attractive limit cycle (ω-limit cycle). If instead all neighbouring trajectories approach it as time approaches negative infinity, then it is an unstable limit cycle (α-limit cycle). If there is a neighbouring tractory which spirals into the limit cycle as time approaches infinity, and another one which spirals into it as time approaches negative infinity, then it is a semi-stable limit cycle. There are also limit cycles which are neither stable, unstable nor semi-stable: for instance, a neighboring trajectory may approach the limit cycle from the outside, but the inside of the limit cycle is approached by a family of other cycles (which wouldn't be limit cycles).
Stable limit cycles are examples of attractors. They imply self-sustained oscillations: the closed trajectory describes perfect periodic behavior of the system, and any small perturbation from this closed trajectory causes the system to return to it, making the system stick to the limit cycle.
Finding limit cycles
Every closed trajectory contains within its interior a stationary point of the system, i.e. a point where . The Bendixson–Dulac theorem and the Poincaré–Bendixson theorem predict the absence or existence, respectively, of limit cycles of two-dimensional nonlinear dynamical systems.
Open problems
Finding limit cycles in general is a very difficult problem. The number of limit cycles of a polynomial differential equation in the plane is the main object of the second part of Hilbert's sixteenth problem. It is unknown, for instance, whether there is any system in the plane where both components of are quadratic polynomials of the two variables, such that the system has more than 4 limit cycles.
See also
References
- Template:Planetmath reference
- Steven H. Strogatz, "Nonlinear Dynamics and Chaos", Addison Wesley publishing company, 1994.
- M. Vidyasagar, "Nonlinear Systems Analysis, second edition, Prentice Hall, Englewood Cliffs, New Jersey 07632.
- Philip Hartman, "Ordinary Differential Equation", Society for Industrial and Applied Mathematics, 2002.
- Witold Hurewicz, "Lectures on Ordinary Differential Equations", Dover, 2002.
- Solomon Lefschetz, "Differential Equations: Geometric Theory", Dover, 2005.
- Lawrence Perko, "Differential Equations and Dynamical Systems", Springer-Verlag, 2006.
- Arthur Mattuck, Limit Cycles: Existence and Non-existence Criteria, MIT Open Courseware http://videolectures.net/mit1803s06_mattuck_lec32/#










