Risk premium: Difference between revisions
Jump to navigation
Jump to search
en>Jschnur m Reverted edits by 37.11.177.144 (talk) identified as unconstructive (HG) |
en>MPG IRA No edit summary |
||
| Line 1: | Line 1: | ||
[[File:Dih4 subgroups (cycle graphs).svg|thumb|360px|[[Hasse diagram]] of the [[lattice of subgroups]] of the [[dihedral group]] [[Dihedral group of order 8|Dih<sub>4</sub>]]<br><br>In the 3-element layer are the maximal subgroups;<br>their intersection (the '''F. s.''') is the central element in the 5-element layer.<br>So Dih<sub>4</sub> has only one non-generating element beyond ''e''.]] | |||
In [[mathematics]], the '''Frattini subgroup''' Φ(''G'') of a [[group (mathematics)|group]] ''G'' is the [[intersection (set theory)|intersection]] of all [[maximal subgroup]]s of ''G''. For the case that ''G'' has no maximal subgroups, for example the [[trivial group]] ''e'' or the [[Prüfer group]], it is defined by Φ(''G'') = ''G''. It is analogous to the [[Jacobson radical]] in the theory of [[ring (mathematics)|rings]], and intuitively can be thought of as the subgroup of "small elements" (see the "non-generator" characterization below). It is named after [[Giovanni Frattini]], who defined the concept in a paper published in 1885. | |||
==Some facts== | |||
*Φ(''G'') is equal to the set of all '''non-generators''' or '''non-generating elements''' of ''G''. A non-generating element of ''G'' is an element that can always be removed from a [[Generating set of a group|generating set]]; that is, an element ''a'' of ''G'' such that whenever ''X'' is a generating set of ''G'' containing ''a'', ''X'' − {''a''} is also a generating set of ''G''. | |||
*Φ(''G'') is always a [[characteristic subgroup]] of ''G''; in particular, it is always a [[normal subgroup]] of ''G''. | |||
*If ''G'' is finite, then Φ(''G'') is [[nilpotent group|nilpotent]]. | |||
*If ''G'' is a finite [[p-group|''p''-group]], then Φ(''G'') = ''G''<sup>''p''</sup> [''G'',''G'']. Thus the Frattini subgroup is the smallest (with respect to inclusion) [[normal subgroup]] ''N'' such that the [[quotient group]] ''G''/''N'' is an [[elementary abelian group]], i.e., [[Group isomorphism|isomorphic]] to a [[direct sum of abelian groups|direct sum]] of [[cyclic group]]s of [[Order (group theory)|order]] ''p''. Moreover, if the quotient group ''G''/Φ(''G'') (also called the ''Frattini quotient'' of ''G'') has order ''p''<sup>k</sup>, then ''k'' is the smallest number of generators for ''G'' (that is the smallest cardinality of a generating set for ''G''). In particular a finite ''p''-group is cyclic [[if and only if]] its Frattini quotient is cyclic (of order ''p''). A finite ''p''-group is elementary abelian if and only if its Frattini subgroup is the [[trivial group]], Φ(''G'') = ''e''. | |||
*If ''H'' and ''K'' are finite, then Φ(''H''x''K'') = Φ(''H'')x Φ(''K''). | |||
An example of a group with nontrivial Frattini subgroup is the [[cyclic group]] ''G'' of order ''p''<sup>2</sup>, where ''p'' is prime, generated by ''a'', say; here, <math>\Phi(G)=\left\langle a^p\right\rangle</math>. | |||
==See also== | |||
*[[Fitting subgroup]] | |||
*[[Socle (mathematics)|Socle]] | |||
==References== | |||
* {{Cite book | |||
| last = Hall | |||
| first = Marshall | |||
| authorlink = Marshall Hall (mathematician) | |||
| coauthors = | |||
| title = The theory of groups | |||
| publisher = Macmillan | |||
| date = 1959 | |||
| location = New York, N.Y. | |||
| pages = | |||
| url = | |||
| doi = | |||
| id = | |||
| isbn = }} (See Chapter 10, especially Section 10.4.) | |||
{{DEFAULTSORT:Frattini Subgroup}} | |||
[[Category:Group theory]] | |||
[[Category:Functional subgroups]] | |||
Revision as of 16:52, 25 January 2014
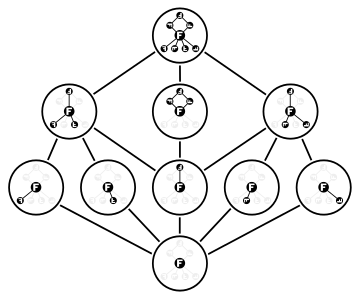
In the 3-element layer are the maximal subgroups;
their intersection (the F. s.) is the central element in the 5-element layer.
So Dih4 has only one non-generating element beyond e.
In mathematics, the Frattini subgroup Φ(G) of a group G is the intersection of all maximal subgroups of G. For the case that G has no maximal subgroups, for example the trivial group e or the Prüfer group, it is defined by Φ(G) = G. It is analogous to the Jacobson radical in the theory of rings, and intuitively can be thought of as the subgroup of "small elements" (see the "non-generator" characterization below). It is named after Giovanni Frattini, who defined the concept in a paper published in 1885.
Some facts
- Φ(G) is equal to the set of all non-generators or non-generating elements of G. A non-generating element of G is an element that can always be removed from a generating set; that is, an element a of G such that whenever X is a generating set of G containing a, X − {a} is also a generating set of G.
- Φ(G) is always a characteristic subgroup of G; in particular, it is always a normal subgroup of G.
- If G is finite, then Φ(G) is nilpotent.
- If G is a finite p-group, then Φ(G) = Gp [G,G]. Thus the Frattini subgroup is the smallest (with respect to inclusion) normal subgroup N such that the quotient group G/N is an elementary abelian group, i.e., isomorphic to a direct sum of cyclic groups of order p. Moreover, if the quotient group G/Φ(G) (also called the Frattini quotient of G) has order pk, then k is the smallest number of generators for G (that is the smallest cardinality of a generating set for G). In particular a finite p-group is cyclic if and only if its Frattini quotient is cyclic (of order p). A finite p-group is elementary abelian if and only if its Frattini subgroup is the trivial group, Φ(G) = e.
- If H and K are finite, then Φ(HxK) = Φ(H)x Φ(K).
An example of a group with nontrivial Frattini subgroup is the cyclic group G of order p2, where p is prime, generated by a, say; here, .
See also
References
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 (See Chapter 10, especially Section 10.4.)
