Calculus of communicating systems

In mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related (called incident in this context) and 0 if they are not. There are variations; see below.

Graph theory

Incidence matrices are mostly used in graph theory.

Undirected and directed graphs

An undirected graph

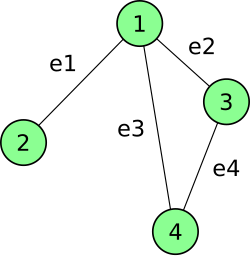
In graph theory an undirected graph G has two kinds of incidence matrices: unoriented and oriented. The incidence matrix (or unoriented incidence matrix) of G is a p × q matrix $(b_{ij})$, where p and q are the numbers of vertices and edges respectively, such that $b_{ij}=1$ if the vertex $v_i$ and edge $x_j$ are incident and 0 otherwise.

For example the incidence matrix of the undirected graph shown on the right is a matrix consisting of 4 rows (corresponding to the four vertices, 1-4) and 4 columns (corresponding to the four edges, e1-e4):

$\left(\begin{array}{cccc}1& 1& 1& 0\\ 1& 0& 0& 0\\ 0& 1& 0& 1\\ 0& 0& 1& 1\\ \end{array}\right)$

If we look at the incidence matrix, we see that the sum of each column is equal to 2. This is because each edge has a vertex connected to each end.

The incidence matrix of a directed graph D is a p × q matrix $[b_{ij}]$ where p and q are the number of vertices and edges respectively, such that $b_{ij}=-1$ if the edge $x_j$ leaves vertex $v_i$, $1$ if it enters vertex $v_i$ and 0 otherwise (Note that many authors use the opposite sign convention.).

An oriented incidence matrix of an undirected graph G is the incidence matrix, in the sense of directed graphs, of any orientation of G. That is, in the column of edge e, there is one +1 in the row corresponding to one vertex of e and one −1 in the row corresponding to the other vertex of e, and all other rows have 0. All oriented incidence matrices of G differ only by negating some set of columns. In many uses, this is an insignificant difference, so one can speak of the oriented incidence matrix, even though that is technically incorrect.

The oriented or unoriented incidence matrix of a graph G is related to the adjacency matrix of its line graph L(G) by the following theorem:

$A(L(G))=B(G{)}^{T}B(G)-2I_q$

where $A(L(G))$ is the adjacency matrix of the line graph of G, B(G) is the incidence matrix, and $I_q$ is the identity matrix of dimension q.

The Kirchhoff matrix is obtained from the oriented incidence matrix M(G) by the formula

$M(G)M(G{)}^T.$

The integral cycle space of a graph is equal to the null space of its oriented incidence matrix, viewed as a matrix over the integers or real or complex numbers. The binary cycle space is the null space of its oriented or unoriented incidence matrix, viewed as a matrix over the two-element field.

Signed and bidirected graphs

The incidence matrix of a signed graph is a generalization of the oriented incidence matrix. It is the incidence matrix of any bidirected graph that orients the given signed graph. The column of a positive edge has a +1 in the row corresponding to one endpoint and a −1 in the row corresponding to the other endpoint, just like an edge in an ordinary (unsigned) graph. The column of a negative edge has either a +1 or a −1 in both rows. The line graph and Kirchhoff matrix properties generalize to signed graphs.

Multigraphs

The definitions of incidence matrix apply to graphs with loops and multiple edges. The column of an oriented incidence matrix that corresponds to a loop is all zero, unless the graph is signed and the loop is negative; then the column is all zero except for ±2 in the row of its incident vertex.

Hypergraphs

Because the edges of ordinary graphs can only have two vertices (one at each end), the column of an incidence matrix for graphs can only have two non-zero entries. By contrast, a hypergraph can have multiple vertices assigned to one edge; thus, the general case describes a hypergraph.

Incidence structures

The incidence matrix of an incidence structure C is a p × q matrix $[b_{ij}]$, where p and q are the number of points and lines respectively, such that $b_{ij}=1$ if the point $p_i$ and line $L_j$ are incident and 0 otherwise. In this case the incidence matrix is also a biadjacency matrix of the Levi graph of the structure. As there is a hypergraph for every Levi graph, and vice-versa, the incidence matrix of an incidence structure describes a hypergraph.

Finite geometries

An important example is a finite geometry. For instance, in a finite plane, X is the set of points and Y is the set of lines. In a finite geometry of higher dimension, X could be the set of points and Y could be the set of subspaces of dimension one less than the dimension of Y; or X could be the set of all subspaces of one dimension d and Y the set of all subspaces of another dimension e.

Block designs

Another example is a block design. Here X is a finite set of "points" and Y is a class of subsets of X, called "blocks", subject to rules that depend on the type of design. The incidence matrix is an important tool in the theory of block designs. For instance, it is used to prove the fundamental theorem of symmetric 2-designs, that the number of blocks equals the number of points.

References

• Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
  
  Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
  
  In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
  
  Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
  
  Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
  
  15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
  
  To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010.
• Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (Section 9.2 Incidence matrices, pp. 166-171)
• Jonathan L Gross, Jay Yellen, Graph Theory and its applications, second edition, 2006 (p 97, Incidence Matrices for undirect graphs; p 98, incidence matrices for digraphs)
• 22 year-old Systems Analyst Rave from Merrickville-Wolford, has lots of hobbies and interests including quick cars, property developers in singapore and baking. Always loves visiting spots like Historic Monuments Zone of Querétaro.
  
  Here is my web site - cottagehillchurch.com