Dikinase
The global navigation satellite system (GNSS) positioning for receiver's position is derived through the calculation steps, or algorithm, given below. In essence, a GNSS receiver measures the transmitting time of GNSS signals emitted from four or more GNSS satellites and these measurements are used to obtain its position (i.e., spatial coordinates) and reception time.
Calculation steps
- A global-navigation-satellite-system (GNSS) receiver measures the apparent transmitting time, , or "phase", of GNSS signals emitted from four or more GNSS satellites ( ), simultaneously.[1]
- GNSS satellites broadcast the messages of satellites' ephemeris, , and intrinsic clock bias (i.e., clock advance), as the functions of (atomic) standard time, e.g., GPST.[2]
- The transmitting time of GNSS satellite signals, , is thus derived from the non-closed-form equations and , where is the relativistic clock bias, periodically risen from the satellite's orbital eccentricity and Earth's gravity field.[2] The satellite's position and velocity are determined by as follows: and .
- In the field of GNSS, "geometric range", , is defined as straight range from to in inertial frame (e.g., Earth Centered Inertial (ECI) one), not in rotating frame.[2]
- The receiver's position, , and reception time, , satisfy the light-cone equation of in inertial frame, where is the speed of light. The signal transit time is .
- The above is extended to the satellite-navigation positioning equation, , where is atmospheric delay (= ionospheric delay + tropospheric delay) along signal path and is the measurement error.
- The Gauss–Newton method can be used to solve the nonlinear least-squares problem for the solution: , where . Note that should be regarded as a function of and .
- The posterior distribution of and is proportional to , whose mode is . Their inference is formalized as maximum a posteriori estimation.
- The posterior distribution of is proportional to .
The solution illustrated
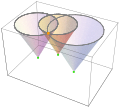
-
Essentially, the solution, , is the intersection of light cones.
-
The posterior distribution of the solution is derived from the product of the distribution of propagating spherical surfaces. (See animation.)
The GPS case
- For Global Positioning System (GPS),[2] the non-closed-form equations in step 3 result in
in which is the orbital eccentric anomaly of satellite , is the mean anomaly, is the eccentricity, and .
- The above can be solved by using the bivariate Newton-Raphson method on and . Two times of iteration will be necessary and sufficient in most cases. Its iterative update will be described by using the approximated inverse of Jacobian matrix as follows:
- Tropospheric delay should not be ignored, while the Global Positioning System (GPS) specification [2] doesn't provide its detailed description.
The GLONASS case
- The GLONASS ephemerides don't provide clock biases , but .
Note
- In the field of GNSS, is called pseudorange, where is a provisional reception time of the receiver. is called receiver's clock bias (i.e., clock advance).[1]
- Standard GNSS receivers output and per an observation epoch.
- The temporal variation in the relativistic clock bias of satellite is linear if its orbit is circular (and thus its velocity is uniform in inertial frame).
- The signal transit time is expressed as , whose right side is round-off-error resistive during calculation.
- The geometric range is calculated as , where the Earth-centred Earth-fixed (ECEF) rotating frame (e.g., WGS84 or ITRF) is used in the right side and is the Earth rotating matrix with the argument of the signal transit time.[2] The matrix can be factorized as .
- The line-of-sight unit vector of satellite observed at is described as: .
- The satellite-navigation positioning equation may be expressed by using the variables and .
- The nonlinearity of the vertical dependency of tropospheric delay degrades the convergence efficiency in the Gauss–Newton iterations in step 7.
- The above notation is different from that in the Wikipedia articles, 'Position calculation introduction' and 'Position calculation advanced', of Global Positioning System (GPS).