Eduard Study

Name: Jodi Junker
My age: 32
Country: Netherlands
Home town: Oudkarspel
Post code: 1724 Xg
Street: Waterlelie 22

my page - www.hostgator1centcoupon.info In geometry, parallel lines are lines in a plane which do not meet. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not intersect or touch at any point are said to be parallel. By extension, a line and a plane, or two planes, in three-dimensional Euclidean space that do not share a point are said to be parallel.

Parallelism is primarily a property of Euclidean space and some related geometries such as affine geometry. Some other spaces, such as hyperbolic space have analogous properties also sometimed referred to as parallelism.

Symbol

The parallel symbol is $\parallel$ . For example, $AB\parallel CD$ indicates that line AB is parallel to line CD.

In the Unicode character set, the "parallel" and "not parallel" signs have codepoints U+2225 (∥) and U+2226 (∦), respectively. In addition, U+22D5 (⋕) represents the relation "equal and parallel to".

Euclidean parallelism

As shown by the tick marks, lines a and b are parallel. This can be proved because the transversal t produces congruent angles.

Given straight lines l and m, the following descriptions of line m equivalently define it as parallel to line l in Euclidean space:

1. Every point on line m is located at exactly the same minimum distance from line l (equidistant lines).
2. Line m is on the same plane as line l but does not intersect l (even assuming that lines extend to infinity in either direction).
3. Lines m and l are both intersected by a third straight line (a transversal) in the same plane, and the corresponding angles of intersection with the transversal are congruent. (This is equivalent to Euclid's parallel postulate.)

In other words, parallel lines must be located in the same plane, and parallel planes must be located in the same three-dimensional space. A parallel combination of a line and a plane may be located in the same three-dimensional space. Lines parallel to each other have the same gradient. Compare to perpendicular.

Construction

The three definitions above lead to three different methods of construction of parallel lines.

The problem: Draw a line through a parallel to l.

• 

  Definition 1: Line m has everywhere the same distance to line l.

• 

  Definition 2: Take a random line through a that intersects l in x. Move point x to infinity.

• 

  Definition 3: Both l and m share a transversal line through a that intersect them at 90°.

Another definition of parallel line that is often used is that two lines are parallel if they do not intersect, though this definition applies only in the 2-dimensional plane. Another easy way is to remember that a parallel line is a line that has an equal distance with the opposite line.

Distance between two parallel lines

Because a parallel line is a line that has an equal distance with the opposite line, there is a unique distance between the two parallel lines. Given the equations of two non-vertical parallel lines

$y=mx+b_{1}\,$

$y=mx+b_{2}\,,$

the distance between the two lines can be found by solving the linear systems

${\begin{cases}y=mx+b_{1}\\y=-x/m\end{cases}}$

and

${\begin{cases}y=mx+b_{2}\\y=-x/m\end{cases}}$

to get the coordinates of the points. The solutions to the linear systems are the points

$\left(x_{1},y_{1}\right)\ =\left({\frac {-b_{1}m}{m^{2}+1}},{\frac {b_{1}}{m^{2}+1}}\right)\,$

and

$\left(x_{2},y_{2}\right)\ =\left({\frac {-b_{2}m}{m^{2}+1}},{\frac {b_{2}}{m^{2}+1}}\right).\,$

The distance between the points is

$d={\sqrt {\left({\frac {b_{1}m-b_{2}m}{m^{2}+1}}\right)^{2}+\left({\frac {b_{2}-b_{1}}{m^{2}+1}}\right)^{2}}}\,,$

which reduces to

$d={\frac {|b_{2}-b_{1}|}{\sqrt {m^{2}+1}}}\,.$

When the lines are given by

$ax+by+c_{1}=0\,$

$ax+by+c_{2}=0,\,$

their distance can be expressed as

$d={\frac {|c_{2}-c_{1}|}{\sqrt {a^{2}+b^{2}}}}.$

Extension to non-Euclidean geometry

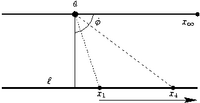
In non-Euclidean geometry, it is more common to talk about geodesics than (straight) lines. A geodesic is the path that a particle follows if no force is applied to it. In non-Euclidean geometry (spherical or hyperbolic) the three Euclidean definitions are not equivalent: only the second one is useful in other non-Euclidean geometries. In general, equidistant lines are not geodesics so the equidistant definition cannot be used. In the Euclidean plane, when two geodesics (straight lines) are intersected with the same angles by a transversal geodesic (see image), every (non-parallel) geodesic intersects them with the same angles. In both the hyperbolic and spherical plane, this is not the case. For example, geodesics sharing a common perpendicular only do so at one point (hyperbolic space) or at two (antipodal) points (spherical space).

In general geometry it is useful to distinguish the three definitions above as three different types of lines, respectively equidistant lines, parallel geodesics and geodesics sharing a common perpendicular.

While in Euclidean geometry two geodesics can either intersect or be parallel, in general and in hyperbolic space in particular there are three possibilities. Two geodesics can be either:

1. intersecting: they intersect in a common point in the plane
2. parallel: they do not intersect in the plane, but do in the limit to infinity
3. ultra parallel: they do not even intersect in the limit to infinity

In the literature ultra parallel geodesics are often called parallel. Geodesics intersecting at infinity are then called limit geodesics.

Spherical

On the spherical plane there is no such thing as a parallel line. Line a is a great circle, the equivalent of a straight line in the spherical plane. Line c is equidistant to line a but is not a great circle. It is a parallel of latitude. Line b is another geodesic which intersects a in two antipodal points. They share two common perpendiculars (one shown in blue).

In the spherical plane, all geodesics are great circles. Great circles divide the sphere in two equal hemispheres and all great circles intersect each other. By the above definitions, there are no parallel geodesics to a given geodesic, all geodesics intersect. Equidistant lines on the sphere are called parallels of latitude in analog to latitude lines on a globe. Parallel lines in Euclidean space are straight lines; equidistant lines are not geodesics and therefore are not directly analogous to straight lines in the Euclidean space. An object traveling along such a line has to accelerate away from the geodesic to which it is equidistant to avoid intersecting with it. When embedded in Euclidean space a dimension higher, parallels of latitude can be generated by the intersection of the sphere with a plane parallel to a plane through the center.

Hyperbolic

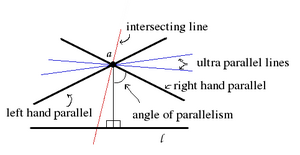
In the hyperbolic plane, there are two lines through a given point that intersect a given line in the limit to infinity. While in Euclidean geometry a geodesic intersects its parallels in both directions in the limit to infinity, in hyperbolic geometry both directions have their own line of parallelism. When visualized on a plane a geodesic is said to have a left-handed parallel and a right-handed parallel through a given point. The angle the parallel lines make with the perpendicular from that point to the given line is called the angle of parallelism. The angle of parallelism depends on the distance of the point to the line with respect to the curvature of the space. The angle is also present in the Euclidean case, there it is always 90° so the left and right-handed parallels coincide. The parallel lines divide the set of geodesics through the point in two sets: intersecting geodesics that intersect the given line in the hyperbolic plane, and ultra parallel geodesics that do not intersect even in the limit to infinity (in either direction). In the Euclidean limit the latter set is empty.

Intersecting, parallel and ultra parallel lines through a with respect to l in the hyperbolic plane. The parallel lines appear to intersect l just off the image. This is an artifact of the visualisation. It is not possible to isometrically embed the hyperbolic plane in three dimensions. In a real hyperbolic space the lines will get closer to each other and 'touch' in infinity.

Benefits of Residing in a Apartment or Landed property in Singapore Property New Launches & Project Showcase In Singapore Many residential Singapore property sales involve buying property in Singapore at new launches. These are often homes underneath building, being sold new by developers. New Launch Singapore Property, 28 Imperial Residences Coming To Geylang Lorong 26 The property market is slowing down, based on personal property transactions in May Cell Apps FREE Sign Up Log in Property Brokers Feedback

Individuals all wish to be seen having the identical foresight as the experts in property investment or the massive names in their own fields. Thus the discharge of these tales works to encourage different buyers to observe suit. Bartley Ridge is the most popular new launch in district 13. Irresistible pricing from $1,1xx psf. Bartley Ridge is a ninety nine-12 months leasehold new condominium at Mount Vernon road, good next to Bartley MRT station (CC12). If you want to get more Rehda Johor chairman Koh Moo Hing said potential property consumers in the two areas Http://Modern.Dowatch.Net/Profile/Mic31K/Created/Topics are now adopting a wait-and-see attitude. How can I get the ebrochure and flooring plans of the new launch projects ? The Existing Mortgage on your HDB District 13, Freehold condominium District 11, Freehold Cluster landed house Sea Horizon EC @ Pasir Ris

FindSgNewLaunch is the main Singapore Property web site - one of the best place to begin your actual estate search whether you might be an investor, shopping for for own use, or searching for a spot to lease. With detailed details about each property, together with maps and pictures. We deliver you probably the most complete choice out there. No. For brand spanking new Singapore property gross sales, you possibly can withdraw at any time earlier than booking the unit, without penalty. On the preview, the agent will let you recognize the exact worth for you to resolve whether or not to proceed or not. Solely when you resolve to proceed will the agent book the unit for you. Pending for Sale Licence Approval All Pending for Sale Licence Approval New launch FREEHOLD condominium @ Braddell New launch condominium combined growth at Yishun PROJECT TITLE

To not worry, we'll hold you in our VIP Precedence list for future new launch VIP Preview. We'll contact you to establish your wants and advocate related tasks, both new launch or resale properties that probably match your standards. In case you're looking for resale property, such as these few years old, or just got Short-term Occupation Permit (PRIME), you might click on here right here for fast search and submit your shortlisted listings to us, we'll check and call you for viewing.

Oceanfront Suites, irresistible pricing for a 946 leasehold property with magnificent sea view. Dreaming of basking and feeling the warmth of pure sunlight is now just a click on away. Oceanfront Suites - Seaside residing no longer needs to remain an unattainable This Cambodia new launch, a mega development has also 762 residential models. Additionally located within this Oxley abroad property is a mega shopping center with 627 outlets and also up to 963 available workplace spaces and is surrounded by quite a few Embassy, resorts, Casinos and many vacationer relax space. Belysa EC @ Pasir Ris Esparina EC @ Sengkang Dell Launches World's first Gender-GEDI Female Entrepreneurship Index on 06/04/thirteen by Istanbul, Turkey. Paris Ris EC @ Paris Ris in search of indication of curiosity.

The developer should open a Venture Account with a financial institution or monetary establishment for every housing venture he undertakes, before he's issued with a Sale License (license to sell models in his development). All payments from buyers before completion of the challenge, and construction loans, go into the mission account. New launch rental LA FIESTA, an thrilling new condominium located along Sengkang Square / Compassvale Highway is a brief stroll to the bustling Sengkang City Centre the place the bus interchange, Sengkang MRT and LRT stations are located. Glorious location,Premium rental with Bayfront resort lifestyle theme and views ofwaterscape. Close to EC pricing - Worth for cash! Apr 02, 2013 Sengkang New Rental Launch, La Fiesta- Sengkang MRTstation at your gate.

As The Hillford property launch at Jalan Jurong Kechil may be very close to to beauty world mrt , the environment for the plot of land which belongs to World Class Land remains very upbeat as it is rather close to to Holland Village. Review now by visiting the brand new apartment pages on our website, each displaying complete particulars and the latest information of each new launch. You can even contact us directly to obtain quick & correct answers to all of your questions with high of the road service. An inevitable conclusion is that costs within the property market have just set new highs. The apparent connotation for potential buyers is to take motion now before prices bounce again. tract and points to his property line, marked by a big maple in a sea of Search SG Developersale.com

Reflexive variant

In synthetic, affine geometry the relation of two parallel lines is a fundamental concept that is modified from the usage in Euclidean geometry. It is clear that the relation of parallelism is a symmetric relation and a transitive relation. These are two properties of an equivalence relation. In Euclidean geometry a line is not considered to be parallel to itself, but in affine geometry it is convenient to hold a line as parallel to itself, thus yielding parallelism as an equivalence relation.

Another way of describing this type of parallelism is the requirement that their intersection is not a singleton. Two lines are then parallel when they have all or none of their points in common. It has been noted that Playfair's axiom used in affine and Euclidean geometry is then equivalent to the statement that parallelism forms a transitive relation on the set of lines in the plane.

See also

• Clifford parallel
• Limiting parallel
• Ultraparallel theorem

Notes and references

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.

External links

• Constructing a parallel line through a given point with compass and straightedge