Dual (category theory): Difference between revisions
en>Vadmium m →References: Category:Duality theories sorting |
dab, per talk page |
||
| Line 1: | Line 1: | ||
{{about|coproducts in categories|"coproduct" in the sense of comultiplication|Coalgebra}} | |||
In [[category theory]], the '''coproduct''', or '''categorical sum''', is a category-theoretic construction which includes as examples the [[disjoint union|disjoint union of sets]] and [[disjoint union (topology)|of topological spaces]], the [[free product|free product of groups]], and the [[direct sum]] of [[Module (mathematics)|modules]] and [[vector space]]s. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a [[morphism]]. It is the category-theoretic [[Dual (category theory)|dual notion]] to the [[product (category theory)|categorical product]], which means the definition is the same as the product but with all [[morphism|arrows]] reversed. Despite this seemingly innocuous change in the name and notation, coproducts can be and typically are dramatically different from products. | |||
==Definition== | |||
The formal definition is as follows: Let ''C'' be a category and let {''X<sub>j</sub>'' : ''j'' ∈ ''J''} be an [[index set|indexed family]] of objects in ''C''. The coproduct of the family {''X<sub>j</sub>''} is an object ''X'' together with a collection of [[morphism]]s ''i<sub>j</sub>'' : ''X<sub>j</sub>'' → ''X'' (called ''[[canonical injection]]s'' although they need not be [[injective function|injections]] or even [[monomorphism|monic]]) which satisfy a [[universal property]]: for any object ''Y'' and any collection of morphisms ''f<sub>j</sub>'' : ''X<sub>j</sub>'' → ''Y'', there exists a unique morphism ''f'' from ''X'' to ''Y'' such that ''f<sub>j</sub>'' = ''f'' ∘ ''i<sub>j</sub>''. That is, the following diagram [[commutative diagram|commutes]] (for each ''j''): | |||
[[Image:Coproduct-01.svg|160px|center]] | |||
The coproduct of the family {''X<sub>j</sub>''} is often denoted | |||
:<math> X = \coprod_{j\in J}X_j</math> | |||
or | |||
:<math>X = \bigoplus_{j \in J} X_j.</math> | |||
Sometimes the morphism ''f'' may be denoted | |||
:<math>f=\coprod_{j \in J} f_j: \coprod_{j \in J} X_j \to Y</math> | |||
to indicate its dependence on the individual ''f''<sub>''j''</sub>. | |||
If the family of objects consists of only two members the coproduct is usually written ''X''<sub>1</sub> ∐ ''X''<sub>2</sub> or ''X''<sub>1</sub> ⊕ ''X''<sub>2</sub> or sometimes simply ''X''<sub>1</sub> + ''X''<sub>2</sub>, and the diagram takes the form: | |||
[[Image:Coproduct-03.svg|280px|center]] | |||
The unique arrow ''f'' making this diagram commute is then correspondingly denoted ''f''<sub>1</sub> ∐ ''f''<sub>2</sub> or ''f''<sub>1</sub> ⊕ ''f''<sub>2</sub> or ''f''<sub>1</sub> + ''f''<sub>2</sub> or [''f''<sub>1</sub>, ''f''<sub>2</sub>]. | |||
== Examples == | |||
The coproduct in the [[category of sets]] is simply the '''[[disjoint union#Set theory definition|disjoint union]]''' with the maps ''i<sub>j</sub>'' being the [[inclusion map]]s. Unlike [[direct product]]s, coproducts in other categories are not all obviously based on the notion for sets, because unions don't behave well with respect to preserving operations (e.g. the union of two groups need not be a group), and so coproducts in different categories can be dramatically different from each other. For example, the coproduct in the [[category of groups]], called the '''[[free product]]''', is quite complicated. On the other hand, in the [[category of abelian groups]] (and equally for [[vector spaces]]), the coproduct, called the '''[[direct sum]]''', consists of the elements of the direct product which have only [[finite set|finitely]] many nonzero terms. (It therefore coincides exactly with the direct product in the case of finitely many factors.) | |||
In the case of [[topological space]]s coproducts are disjoint unions with their [[disjoint union (topology)|disjoint union topologies]]. That is, it is a disjoint union of the underlying sets, and the [[open set]]s are sets ''open in each of the spaces'', in a rather evident sense. In the category of [[pointed space]]s, fundamental in [[homotopy theory]], the coproduct is the [[wedge sum]] (which amounts to joining a collection of spaces with base points at a common base point). | |||
Despite all this dissimilarity, there is still, at the heart of the whole thing, a disjoint union: the direct sum of abelian groups is the group generated by the "almost" disjoint union (disjoint union of all nonzero elements, together with a common zero), similarly for vector spaces: the space [[linear span|spanned]] by the "almost" disjoint union; the free product for groups is generated by the set of all letters from a similar "almost disjoint" union where no two elements from different sets are allowed to commute. | |||
== Discussion == | |||
The coproduct construction given above is actually a special case of a [[colimit]] in category theory. The coproduct in a category ''C'' can be defined as the colimit of any [[functor]] from a [[discrete category]] ''J'' into ''C''. Not every family {''X''<sub>''j''</sub>} will have a coproduct in general, but if it does, then the coproduct is unique in a strong sense: if ''i''<sub>''j''</sub> : ''X''<sub>''j''</sub> → ''X'' and ''k''<sub>''j''</sub> : ''X''<sub>''j''</sub> → ''Y'' are two coproducts of the family {''X''<sub>''j''</sub>}, then (by the definition of coproducts) there exists a unique [[isomorphism]] ''f'' : ''X'' → ''Y'' such that ''fi''<sub>''j''</sub> = ''k''<sub>''j''</sub> for each ''j'' in ''J''. | |||
As with any [[universal property]], the coproduct can be understood as a universal morphism. Let Δ: ''C'' → ''C''×''C'' be the [[diagonal functor]] which assigns to each object ''X'' the [[ordered pair]] (''X'',''X'') and to each morphism ''f'':''X'' → ''Y'' the pair (''f'',''f''). Then the coproduct ''X''+''Y'' in ''C'' is given by a universal morphism to the functor Δ from the object (''X'',''Y'') in ''C''×''C''. | |||
The coproduct indexed by the [[empty set]] (that is, an ''empty coproduct'') is the same as an [[initial object]] in ''C''. | |||
If ''J'' is a set such that all coproducts for families indexed with ''J'' exist, then it is possible to choose the products in a compatible fashion so that the coproduct turns into a functor ''C''<sup>''J''</sup> → ''C''. The coproduct of the family {''X''<sub>''j''</sub>} is then often denoted by ∐<sub>''j''</sub> ''X''<sub>''j''</sub>, and the maps ''i''<sub>''j''</sub> are known as the '''[[inclusion map|natural injections]]'''. | |||
Letting Hom<sub>''C''</sub>(''U'',''V'') denote the set of all morphisms from ''U'' to ''V'' in ''C'' (that is, a [[hom-set]] in ''C''), we have a [[natural isomorphism]] | |||
:<math>\operatorname{Hom}_C\left(\coprod_{j\in J}X_j,Y\right) \cong \prod_{j\in J}\operatorname{Hom}_C(X_j,Y)</math> | |||
given by the [[bijection]] which maps every [[tuple]] of morphisms | |||
:<math>(f_j)_{j\in J} \in \prod_{j \in J}\operatorname{Hom}(X_j,Y)</math> | |||
(a product in '''Set''', the [[category of sets]], which is the [[Cartesian product]], so it is a tuple of morphisms) to the morphism | |||
:<math>\coprod_{j\in J} f_j \in \operatorname{Hom}\left(\coprod_{j\in J}X_j,Y\right).</math> | |||
That this map is a [[surjection]] follows from the commutativity of the diagram: any morphism ''f'' is the coproduct of the tuple | |||
:<math>(f\circ i_j)_{j \in J}.</math> | |||
That it is an injection follows from the universal construction which stipulates the uniqueness of such maps. The naturality of the isomorphism is also a consequence of the diagram. Thus the contravariant [[hom-functor]] changes coproducts into products. Stated another way, the hom-functor, viewed as a functor from the [[opposite category]] ''C''<sup>opp</sup> to '''Set''' is continuous; it preserves limits (a coproduct in ''C'' is a product in ''C''<sup>opp</sup>). | |||
If ''J'' is a [[finite set|finite]] set, say ''J'' = {1,...,''n''}, then the coproduct of objects ''X''<sub>1</sub>,...,''X''<sub>''n''</sub> is often denoted by ''X''<sub>1</sub>⊕...⊕''X''<sub>''n''</sub>. | |||
Suppose all finite coproducts exist in ''C'', coproduct functors have been chosen as above, and 0 denotes the [[initial object]] of ''C'' corresponding to the empty coproduct. We then have [[natural isomorphism]]s | |||
:<math>X\oplus (Y \oplus Z)\cong (X\oplus Y)\oplus Z\cong X\oplus Y\oplus Z</math> | |||
:<math>X\oplus 0 \cong 0\oplus X \cong X</math> | |||
:<math>X\oplus Y \cong Y\oplus X.</math> | |||
These properties are formally similar to those of a commutative [[monoid]]; a category with finite coproducts is an example of a symmetric [[monoidal category]]. | |||
If the category has a [[zero object]] ''Z'', then we have unique morphism ''X'' → ''Z'' (since ''Z'' is [[terminal object|terminal]]) and thus a morphism ''X'' ⊕ ''Y'' → ''Z'' ⊕ ''Y''. Since ''Z'' is also initial, we have a canonical isomorphism ''Z'' ⊕ ''Y'' ≅ ''Y'' as in the preceding paragraph. We thus have morphisms ''X'' ⊕ ''Y'' → ''X'' and ''X'' ⊕ ''Y'' → ''Y'', by which we infer a canonical morphism ''X'' ⊕ ''Y'' → ''X''×''Y''. This may be extended by induction to a canonical morphism from any finite coproduct to the corresponding product. This morphism need not in general be an isomorphism; in '''Grp''' it is a proper [[epimorphism]] while in '''Set'''<sub>*</sub> (the category of [[pointed set]]s) it is a proper [[monomorphism]]. In any [[preadditive category]], this morphism is an isomorphism and the corresponding object is known as the [[biproduct]]. A category with all finite biproducts is known as an [[additive category]]. | |||
If all families of objects indexed by ''J'' have coproducts in ''C'', then the coproduct comprises a functor ''C''<sup>''J''</sup> → ''C''. Note that, like the product, this functor is ''covariant''. | |||
==See also== | |||
*[[Product (category theory)|Product]] | |||
*[[Limit (category theory)|Limits and colimits]] | |||
*[[Coequalizer]] | |||
*[[Direct limit]] | |||
==References== | |||
* {{cite book | last=Mac Lane | first=Saunders | authorlink=Saunders Mac Lane | title=[[Categories for the Working Mathematician]] | edition=2nd | series=[[Graduate Texts in Mathematics]] | volume=5 | location=New York, NY | publisher=[[Springer-Verlag]] | year=1998 | isbn=0-387-98403-8 | zbl=0906.18001 }} | |||
== External links == | |||
*[http://www.j-paine.org/cgi-bin/webcats/webcats.php Interactive Web page ] which generates examples of coproducts in the category of finite sets. Written by [http://www.j-paine.org/ Jocelyn Paine]. | |||
[[Category:Limits (category theory)]] | |||
Revision as of 07:16, 30 November 2013
29 yr old Orthopaedic Surgeon Grippo from Saint-Paul, spends time with interests including model railways, top property developers in singapore developers in singapore and dolls. Finished a cruise ship experience that included passing by Runic Stones and Church.
In category theory, the coproduct, or categorical sum, is a category-theoretic construction which includes as examples the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a morphism. It is the category-theoretic dual notion to the categorical product, which means the definition is the same as the product but with all arrows reversed. Despite this seemingly innocuous change in the name and notation, coproducts can be and typically are dramatically different from products.
Definition
The formal definition is as follows: Let C be a category and let {Xj : j ∈ J} be an indexed family of objects in C. The coproduct of the family {Xj} is an object X together with a collection of morphisms ij : Xj → X (called canonical injections although they need not be injections or even monic) which satisfy a universal property: for any object Y and any collection of morphisms fj : Xj → Y, there exists a unique morphism f from X to Y such that fj = f ∘ ij. That is, the following diagram commutes (for each j):

The coproduct of the family {Xj} is often denoted
or
Sometimes the morphism f may be denoted
to indicate its dependence on the individual fj.
If the family of objects consists of only two members the coproduct is usually written X1 ∐ X2 or X1 ⊕ X2 or sometimes simply X1 + X2, and the diagram takes the form:
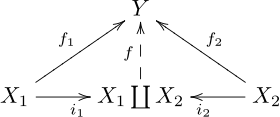
The unique arrow f making this diagram commute is then correspondingly denoted f1 ∐ f2 or f1 ⊕ f2 or f1 + f2 or [f1, f2].
Examples
The coproduct in the category of sets is simply the disjoint union with the maps ij being the inclusion maps. Unlike direct products, coproducts in other categories are not all obviously based on the notion for sets, because unions don't behave well with respect to preserving operations (e.g. the union of two groups need not be a group), and so coproducts in different categories can be dramatically different from each other. For example, the coproduct in the category of groups, called the free product, is quite complicated. On the other hand, in the category of abelian groups (and equally for vector spaces), the coproduct, called the direct sum, consists of the elements of the direct product which have only finitely many nonzero terms. (It therefore coincides exactly with the direct product in the case of finitely many factors.)
In the case of topological spaces coproducts are disjoint unions with their disjoint union topologies. That is, it is a disjoint union of the underlying sets, and the open sets are sets open in each of the spaces, in a rather evident sense. In the category of pointed spaces, fundamental in homotopy theory, the coproduct is the wedge sum (which amounts to joining a collection of spaces with base points at a common base point).
Despite all this dissimilarity, there is still, at the heart of the whole thing, a disjoint union: the direct sum of abelian groups is the group generated by the "almost" disjoint union (disjoint union of all nonzero elements, together with a common zero), similarly for vector spaces: the space spanned by the "almost" disjoint union; the free product for groups is generated by the set of all letters from a similar "almost disjoint" union where no two elements from different sets are allowed to commute.
Discussion
The coproduct construction given above is actually a special case of a colimit in category theory. The coproduct in a category C can be defined as the colimit of any functor from a discrete category J into C. Not every family {Xj} will have a coproduct in general, but if it does, then the coproduct is unique in a strong sense: if ij : Xj → X and kj : Xj → Y are two coproducts of the family {Xj}, then (by the definition of coproducts) there exists a unique isomorphism f : X → Y such that fij = kj for each j in J.
As with any universal property, the coproduct can be understood as a universal morphism. Let Δ: C → C×C be the diagonal functor which assigns to each object X the ordered pair (X,X) and to each morphism f:X → Y the pair (f,f). Then the coproduct X+Y in C is given by a universal morphism to the functor Δ from the object (X,Y) in C×C.
The coproduct indexed by the empty set (that is, an empty coproduct) is the same as an initial object in C.
If J is a set such that all coproducts for families indexed with J exist, then it is possible to choose the products in a compatible fashion so that the coproduct turns into a functor CJ → C. The coproduct of the family {Xj} is then often denoted by ∐j Xj, and the maps ij are known as the natural injections.
Letting HomC(U,V) denote the set of all morphisms from U to V in C (that is, a hom-set in C), we have a natural isomorphism
given by the bijection which maps every tuple of morphisms
(a product in Set, the category of sets, which is the Cartesian product, so it is a tuple of morphisms) to the morphism
That this map is a surjection follows from the commutativity of the diagram: any morphism f is the coproduct of the tuple
That it is an injection follows from the universal construction which stipulates the uniqueness of such maps. The naturality of the isomorphism is also a consequence of the diagram. Thus the contravariant hom-functor changes coproducts into products. Stated another way, the hom-functor, viewed as a functor from the opposite category Copp to Set is continuous; it preserves limits (a coproduct in C is a product in Copp).
If J is a finite set, say J = {1,...,n}, then the coproduct of objects X1,...,Xn is often denoted by X1⊕...⊕Xn. Suppose all finite coproducts exist in C, coproduct functors have been chosen as above, and 0 denotes the initial object of C corresponding to the empty coproduct. We then have natural isomorphisms
These properties are formally similar to those of a commutative monoid; a category with finite coproducts is an example of a symmetric monoidal category.
If the category has a zero object Z, then we have unique morphism X → Z (since Z is terminal) and thus a morphism X ⊕ Y → Z ⊕ Y. Since Z is also initial, we have a canonical isomorphism Z ⊕ Y ≅ Y as in the preceding paragraph. We thus have morphisms X ⊕ Y → X and X ⊕ Y → Y, by which we infer a canonical morphism X ⊕ Y → X×Y. This may be extended by induction to a canonical morphism from any finite coproduct to the corresponding product. This morphism need not in general be an isomorphism; in Grp it is a proper epimorphism while in Set* (the category of pointed sets) it is a proper monomorphism. In any preadditive category, this morphism is an isomorphism and the corresponding object is known as the biproduct. A category with all finite biproducts is known as an additive category.
If all families of objects indexed by J have coproducts in C, then the coproduct comprises a functor CJ → C. Note that, like the product, this functor is covariant.
See also
References
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
External links
- Interactive Web page which generates examples of coproducts in the category of finite sets. Written by Jocelyn Paine.









