Finite difference: Difference between revisions
en>Arthur Rubin Undid revision 507664200 by Florian Xaver (talk) Actually, not. (x)_1 = x |
|||
| Line 1: | Line 1: | ||
{{More footnotes|date=March 2013}} | |||
In [[category theory]], a branch of [[mathematics]], the abstract notion of a '''limit''' captures the essential properties of universal constructions such as [[product (category theory)|products]], [[pullback (category theory)|pullbacks]] and [[inverse limit]]s. The [[duality (category theory)|dual notion]] of a '''colimit''' generalizes constructions such as [[disjoint union]]s, [[direct sum]]s, [[coproduct]]s, [[pushout (category theory)|pushout]]s and [[direct limit]]s. | |||
Limits and colimits, like the strongly related notions of [[universal property|universal properties]] and [[adjoint functors]], exist at a high level of abstraction. In order to understand them, it is helpful to first study the specific examples these concepts are meant to generalize. | |||
== Definition == | |||
Limits and colimits in a [[category (mathematics)|category]] ''C'' are defined by means of diagrams in ''C''. Formally, a '''[[diagram (category theory)|diagram]]''' of type ''J'' in ''C'' is a [[functor]] from ''J'' to ''C'': | |||
:''F'' : ''J'' → ''C''. | |||
The category ''J'' is thought of as [[index category]], and the diagram ''F'' is thought of as indexing a collection of objects and [[morphism]]s in ''C'' patterned on ''J''. The actual objects and morphisms in ''J'' are largely irrelevant—only the way in which they are interrelated matters. | |||
One is most often interested in the case where the category ''J'' is a [[small category|small]] or even [[Finite set|finite]] category. A diagram is said to be '''small''' or '''finite''' whenever ''J'' is. | |||
===Limits=== | |||
Let ''F'' : ''J'' → ''C'' be a diagram of type ''J'' in a category ''C''. A '''[[cone (category theory)|cone]]''' to ''F'' is an object ''N'' of ''C'' together with a family ψ<sub>''X''</sub> : ''N'' → ''F''(''X'') of morphisms indexed by the objects ''X'' of ''J'', such that for every morphism ''f'' : ''X'' → ''Y'' in ''J'', we have ''F''(''f'') o ψ<sub>''X''</sub> = ψ<sub>''Y''</sub>. | |||
A '''limit''' of the diagram ''F'' : ''J'' → ''C'' is a cone (''L'', φ) to ''F'' such that for any other cone (''N'', ψ) to ''F'' there exists a ''unique'' morphism ''u'' : ''N'' → ''L'' such that φ<sub>''X''</sub> o ''u'' = ψ<sub>''X''</sub> for all ''X'' in ''J''. | |||
[[File:Functor cone (extended).svg|center|A universal cone]] | |||
One says that the cone (''N'', ψ) factors through the cone (''L'', φ) with | |||
the unique factorization ''u''. The morphism ''u'' is sometimes called the '''mediating morphism'''. | |||
Limits are also referred to as ''[[universal cone]]s'', since they are characterized by a [[universal property]] (see below for more information). As with every universal property, the above definition describes a balanced state of generality: The limit object ''L'' has to be general enough to allow any other cone to factor through it; on the other hand, ''L'' has to be sufficiently specific, so that only ''one'' such factorization is possible for every cone. | |||
Limits may also be characterized as [[terminal object]]s in the [[category of cones]] to ''F''. | |||
It is possible that a diagram does not have a limit at all. However, if a diagram does have a limit then this limit is essentially unique: it is unique [[up to]] a unique [[isomorphism]]. For this reason one often speaks of ''the'' limit of ''F''. | |||
===Colimits=== | |||
The [[Dual (category theory)|dual notions]] of limits and cones are colimits and co-cones. Although it is straightforward to obtain the definitions of these by inverting all morphisms in the above definitions, we will explicitly state them here: | |||
A '''[[co-cone]]''' of a diagram ''F'' : ''J'' → ''C'' is an object ''N'' of ''C'' together with a family of morphisms | |||
:ψ<sub>''X''</sub> : ''F''(''X'') → ''N'' | |||
for every object ''X'' of ''J'', such that for every morphism ''f'' : ''X'' → ''Y'' in ''J'', we have ψ<sub>''Y''</sub> o ''F''(''f'')= ψ<sub>''X''</sub>. | |||
A '''colimit''' of a diagram ''F'' : ''J'' → ''C'' is a co-cone (''L'', <math>\phi</math>) of ''F'' such that for any other co-cone (''N'', ψ) of ''F'' there exists a unique morphism ''u'' : ''L'' → ''N'' such that ''u'' o <math>\phi</math><sub>''X''</sub> = ψ<sub>''X''</sub> for all ''X'' in ''J''. | |||
[[File:Functor co-cone (extended).svg|center|A universal co-cone]] | |||
Colimits are also referred to as ''[[universal co-cone]]s''. They can be characterized as [[initial object]]s in the [[category of co-cones]] from ''F''. | |||
As with limits, if a diagram ''F'' has a colimit then this colimit is unique up to a unique isomorphism. | |||
===Variations=== | |||
Limits and colimits can also be defined for collections of objects and morphisms without the use of diagrams. The definitions are the same (note that in definitions above we never needed to use composition of morphisms in ''J''). This variation, however, adds no new information. Any collection of objects and morphisms defines a (possibly large) [[directed graph]] ''G''. If we let ''J'' be the [[free category]] generated by ''G'', there is a universal diagram ''F'' : ''J'' → ''C'' whose image contains ''G''. The limit (or colimit) of this diagram is the same as the limit (or colimit) of the original collection of objects and morphisms. | |||
'''Weak limit''' and '''weak colimits''' are defined like limits and colimits, except that the uniqueness property of the mediating morphism is dropped. | |||
==Examples== | |||
===Limits=== | |||
The definition of limits is general enough to subsume several constructions useful in practical settings. In the following we will consider the limit (''L'', φ) of a diagram ''F'' : ''J'' → ''C''. | |||
*'''[[Terminal object]]s'''. If ''J'' is the empty category there is only one diagram of type ''J'': the empty one (similar to the [[empty function]] in set theory). A cone to the empty diagram is essentially just an object of ''C''. The limit of ''F'' is any object that is uniquely factored through by every other object. This is just the definition of a ''terminal object''. | |||
*'''[[Product (category theory)|Products]]'''. If ''J'' is a [[discrete category]] then a diagram ''F'' is essentially nothing but a [[indexed family|family]] of objects of ''C'', indexed by ''J''. The limit ''L'' of ''F'' is called the ''product'' of these objects. The cone φ consists of a family of morphisms φ<sub>''X''</sub> : ''L'' → ''F''(''X'') called the ''projections'' of the product. In the [[category of sets]], for instance, the products are given by [[Cartesian product]]s and the projections are just the natural projections onto the various factors. | |||
**'''Powers'''. A special case of a product is when the diagram ''F'' is a constant functor to an object ''X'' of ''C''. The limit of this diagram is called the ''J<sup>th</sup> power'' of ''X'' and denoted ''X''<sup>''J''</sup>. | |||
*'''[[Equalizer (mathematics)|Equalizer]]s'''. If ''J'' is a category with two objects and two parallel morphisms from object ''1'' to object ''2'' then a diagram of type ''J'' is a pair of parallel morphisms in ''C''. The limit ''L'' of such a diagram is called an ''equalizer'' of those morphisms. | |||
**'''[[Kernel (category theory)|Kernel]]s'''. A ''kernel'' is a special case of an equalizer where one of the morphisms is a [[zero morphism]]. | |||
*'''[[Pullback (category theory)|Pullbacks]]'''. Let ''F'' be a diagram that picks out three objects ''X'', ''Y'', and ''Z'' in ''C'', where the only non-identity morphisms are ''f'' : ''X'' → ''Z'' and ''g'' : ''Y'' → ''Z''. The limit ''L'' of ''F'' is called a ''pullback'' or a ''fiber product''. It can nicely be visualized as a [[commutative diagram|commutative square]]: | |||
[[Image:CategoricalPullback-01.png|center]] | |||
*'''[[Inverse limit]]s'''. Let ''J'' be a [[directed set|directed]] [[poset]] (considered as a small category by adding arrows ''i'' → ''j'' if and only if ''i'' ≤ ''j'') and let ''F'' : ''J''<sup>op</sup> → ''C'' be a diagram. The limit of ''F'' is called (confusingly) an ''inverse limit'', ''projective limit'', or ''directed limit''. | |||
*If ''J'' = '''1''', the category with a single object and morphism, then a diagram of type ''J'' is essentially just an object ''X'' of ''C''. A cone to an object ''X'' is just a morphism with codomain ''X''. A morphism ''f'' : ''Y'' → ''X'' is a limit of the diagram ''X'' if and only if ''f'' is an [[isomorphism]]. More generally, if ''J'' is any category with an [[initial object]] ''i'', then any diagram of type ''J'' has a limit, namely any object isomorphic to ''F''(''i''). Such an isomorphism uniquely determines a universal cone to ''F''. | |||
*'''Topological limits'''. Limits of functions are a special case of [[Filter_(mathematics)#Convergent_filter_bases|limits of filters]], which are related to categorical limits as follows. Given a [[topological space]] ''X'', denote ''F'' the set of filters on ''X'', ''x'' ∈ ''X'' a point, ''V''(''x'') ∈ ''F'' the [[Filter_(mathematics)#Neighbourhood_bases|neighborhood filter]] of ''x'', ''A'' ∈ ''F'' a particular filter and <math>F_{x,A}=\{G\in F \mid V(x)\cup A \subset G\} </math> the set of filters finer than ''A'' and that converge to ''x''. The filters ''F'' are given a small and thin category structure by adding an arrow ''A'' → ''B'' if and only if ''A'' ⊆ ''B''. The injection <math>I_{x,A}:F_{x,A}\to F</math> becomes a functor and the following equivalence holds : | |||
:: ''x'' is a topological limit of ''A'' if and only if ''A'' is a categorical limit of <math>I_{x,A}</math> | |||
===Colimits=== | |||
Examples of colimits are given by the dual versions of the examples above: | |||
*'''[[Initial object]]s''' are colimits of empty diagrams. | |||
*'''[[Coproduct]]s''' are colimits of diagrams indexed by discrete categories. | |||
**'''Copowers''' are colimits of constant diagrams from discrete categories. | |||
*'''[[Coequalizer]]s''' are colimits of a parallel pair of morphisms. | |||
**'''[[Cokernel]]s''' are coequalizers of a morphism and a parallel zero morphism. | |||
*'''[[Pushout (category theory)|Pushouts]]''' are colimits of a pair of morphisms with common domain. | |||
*'''[[Direct limit]]s''' are colimits of diagrams indexed by directed sets. | |||
== Properties == | |||
=== Existence of limits === | |||
A given diagram ''F'' : ''J'' → ''C'' may or may not have a limit (or colimit) in ''C''. Indeed, there may not even be a cone to ''F'', let alone a universal cone. | |||
A category ''C'' is said to '''have limits of type ''J''''' if every diagram of type ''J'' has a limit in ''C''. Specifically, a category ''C'' is said to | |||
*'''have products''' if it has limits of type ''J'' for every ''small'' discrete category ''J'' (it need not have large products), | |||
*'''have equalizers''' if it has limits of type <math>\bullet\rightrightarrows\bullet</math> (i.e. every parallel pair of morphisms has an equalizer), | |||
*'''have pullbacks''' if it has limits of type <math>\bullet\rightarrow\bullet\leftarrow\bullet</math> (i.e. every pair of morphisms with common codomain has a pullback). | |||
A '''[[complete category]]''' is a category that has all small limits (i.e. all limits of type ''J'' for every small category ''J''). | |||
One can also make the dual definitions. A category '''has colimits of type ''J''''' if every diagram of type ''J'' has a colimit in ''C''. A '''[[cocomplete category]]''' is one that has all small colimits. | |||
The '''existence theorem for limits''' states that if a category ''C'' has equalizers and all products indexed by the classes Ob(''J'') and Hom(''J''), then ''C'' has all limits of type ''J''. In this case, the limit of a diagram ''F'' : ''J'' → ''C'' can be constructed as the equalizer of the two morphisms | |||
:<math>s,t : \prod_{i\in\mathrm{Ob}(J)}F(i) \rightrightarrows \prod_{f\in\mathrm{Hom}(J)} F(\mathrm{cod}(f))</math> | |||
given (in component form) by | |||
:<math>\begin{align} | |||
s &= \bigl( F(f)\circ\pi_{F(\mathrm{dom}(f))}\bigr)_{f\in\mathrm{Hom}(J)} \\ | |||
t &= \bigl( \pi_{F(\mathrm{cod}(f))}\bigr)_{f\in\mathrm{Hom}(J)}. | |||
\end{align}</math> | |||
There is a dual '''existence theorem for colimits''' in terms of coequalizers and coproducts. Both of these theorems give sufficient but not necessary conditions for the existence of all (co)limits of type ''J''. | |||
=== Universal property === | |||
Limits and colimits are important special cases of [[universal construction]]s. Let ''C'' be a category and let ''J'' be a small index category. The [[functor category]] ''C''<sup>''J''</sup> may be thought of the category of all diagrams of type ''J'' in ''C''. The ''[[diagonal functor]]'' | |||
:<math>\Delta : \mathcal C \to \mathcal C^{\mathcal J}</math> | |||
is the functor that maps each object ''N'' in ''C'' to the constant functor Δ(''N'') : ''J'' → ''C'' to ''N''. That is, Δ(''N'')(''X'') = ''N'' for each object ''X'' in ''J'' and Δ(''N'')(''f'') = id<sub>''N''</sub> for each morphism ''f'' in ''J''. | |||
Given a diagram ''F'': ''J'' → ''C'' (thought of as an object in ''C''<sup>''J''</sup>), a [[natural transformation]] ψ : Δ(''N'') → ''F'' (which is just a morphism in the category ''C''<sup>''J''</sup>) is the same thing as a cone from ''N'' to ''F''. The components of ψ are the morphisms ψ<sub>''X''</sub> : ''N'' → ''F''(''X''). Dually, a natural transformation ψ : ''F'' → Δ(''N'') is the same thing as a co-cone from ''F'' to ''N''. | |||
The definitions of limits and colimits can then be restated in the form: | |||
*A limit of ''F'' is a universal morphism from Δ to ''F''. | |||
*A colimit of ''F'' is a universal morphism from ''F'' to Δ. | |||
=== Adjunctions === | |||
Like all universal constructions, the formation of limits and colimits is functorial in nature. In other words, if every diagram of type ''J'' has a limit in ''C'' (for ''J'' small) there exists a '''limit functor''' | |||
:<math>\mathrm{lim} : \mathcal{C}^\mathcal{J} \to \mathcal{C}</math> | |||
which assigns each diagram its limit and each [[natural transformation]] η : ''F'' → ''G'' the unique morphism lim η : lim ''F'' → lim ''G'' commuting with the corresponding universal cones. This functor is [[right adjoint]] to the diagonal functor Δ : ''C'' → ''C''<sup>''J''</sup>. | |||
This adjunction gives a bijection between the set of all morphisms from ''N'' to lim ''F'' and the set of all cones from ''N'' to ''F'' | |||
:<math>\mathrm{Hom}(N,\mathrm{lim}F) \cong \mathrm{Cone}(N,F)</math> | |||
which is natural in the variables ''N'' and ''F''. The counit of this adjunction is simply the universal cone from lim ''F'' to ''F''. If the index category ''J'' is [[connected category|connected]] (and nonempty) then the unit of the adjunction is an isomorphism so that lim is a left inverse of Δ. This fails if ''J'' is not connected. For example, if ''J'' is a discrete category, the components of the unit are the [[diagonal morphism]]s δ : ''N'' → ''N''<sup>''J''</sup>. | |||
Dually, if every diagram of type ''J'' has a colimit in ''C'' (for ''J'' small) there exists a '''colimit functor''' | |||
:<math>\mathrm{colim} : \mathcal{C}^\mathcal{J} \to \mathcal{C}</math> | |||
which assigns each diagram its colimit. This functor is [[left adjoint]] to the diagonal functor Δ : ''C'' → ''C''<sup>''J''</sup>, and one has a natural isomorphism | |||
:<math>\mathrm{Hom}(\mathrm{colim}F,N) \cong \mathrm{Cocone}(F,N).</math> | |||
The unit of this adjunction is the universal cocone from ''F'' to colim ''F''. If ''J'' is connected (and nonempty) then the counit is an isomorphism, so that colim is a left inverse of Δ. | |||
Note that both the limit and the colimit functors are [[covariant functor|''covariant'']] functors. | |||
=== As representations of functors === | |||
One can use [[Hom functor]]s to relate limits and colimits in a category ''C'' to limits in '''Set''', the [[category of sets]]. This follows, in part, from the fact the covariant Hom functor Hom(''N'', –) : ''C'' → '''Set''' [[#Preservation of limits|preserves all limits]] in ''C''. By duality, the contravariant Hom functor must take colimits to limits. | |||
If a diagram ''F'' : ''J'' → ''C'' has a limit in ''C'', denoted by lim ''F'', there is a [[canonical isomorphism]] | |||
:<math>\mathrm{Hom}(N,\mathrm{lim} F)\cong\mathrm{lim}\,\mathrm{Hom}(N,F-)</math> | |||
which is natural in the variable ''N''. Here the functor Hom(''N'', ''F''–) is the composition of the Hom functor Hom(''N'', –) with ''F''. This isomorphism is the unique one which respects the limiting cones. | |||
One can use the above relationship to define the limit of ''F'' in ''C''. The first step is to observe that the limit of the functor Hom(''N'', ''F''–) can be identified with the set of all cones from ''N'' to ''F'': | |||
:<math>\mathrm{lim}\,\mathrm{Hom}(N,F-) = \mathrm{Cone}(N,F).</math> | |||
The limiting cone is given by the family of maps π<sub>''X''</sub> : Cone(''N'', ''F'') → Hom(''N'', ''FX'') where π<sub>''X''</sub>(ψ) = ψ<sub>''X''</sub>. If one is given an object ''L'' of ''C'' together with a [[natural isomorphism]] Φ : Hom(–, ''L'') → Cone(–, ''F''), the object ''L'' will be a limit of ''F'' with the limiting cone given by Φ<sub>''L''</sub>(id<sub>''L''</sub>). In fancy language, this amounts to saying that a limit of ''F'' is a [[representable functor|representation]] of the functor Cone(–, ''F'') : ''C'' → '''Set'''. | |||
Dually, if a diagram ''F'' : ''J'' → ''C'' has a colimit in ''C'', denoted colim ''F'', there is a unique canonical isomorphism | |||
:<math>\mathrm{Hom}(\mathrm{colim} F, N)\cong\mathrm{lim}\,\mathrm{Hom}(F-,N)</math> | |||
which is natural in the variable ''N'' and respects the colimiting cones. Identifying the limit of Hom(''F''–, ''N'') with the set Cocone(''F'', ''N''), this relationship can be used to define the colimit of the diagram ''F'' as a representation of the functor Cocone(''F'', –). | |||
=== Interchange of limits and colimits of sets=== | |||
Let ''I'' be a finite category and ''J'' be a small [[filtered category]]. For any [[bifunctor]] | |||
:''F'' : ''I'' × ''J'' → '''Set''' | |||
there is a [[natural isomorphism]] | |||
:<math>\mathrm{colim}_J\,\mathrm{lim}_I F(i, j) \rightarrow \mathrm{lim}_I\,\mathrm{colim}_J F(i, j).</math> | |||
In words, filtered colimits in '''Set''' commute with finite limits. | |||
==Functors and limits== | |||
If ''F'' : ''J'' → ''C'' is a diagram in ''C'' and ''G'' : ''C'' → ''D'' is a [[functor]] then by composition (recall that a diagram is just a functor) one obtains a diagram ''GF'' : ''J'' → ''D''. A natural question is then: | |||
:“How are the limits of ''GF'' related to those of ''F''?” | |||
===Preservation of limits=== | |||
A functor ''G'' : ''C'' → ''D'' induces a map from Cone(''F'') to Cone(''GF''): if Ψ is a cone from ''N'' to ''F'' then ''G''Ψ is a cone from ''GN'' to ''GF''. The functor ''G'' is said to '''preserve the limits of ''F''''' if (''GL'', ''G''φ) is a limit of ''GF'' whenever (''L'', φ) is a limit of ''F''. (Note that if the limit of ''F'' does not exist, then ''G'' [[vacuous truth|vacuously]] preserves the limits of ''F''.) | |||
A functor ''G'' is said to '''preserve all limits of type ''J''''' if it preserves the limits of all diagrams ''F'' : ''J'' → ''C''. For example, one can say that ''G'' preserves products, equalizers, pullbacks, etc. A '''continuous functor''' is one that preserves all ''small'' limits. | |||
One can make analogous definitions for colimits. For instance, a functor ''G'' preserves the colimits of ''F'' if ''G''(''L'', φ) is a colimit of ''GF'' whenever (''L'', φ) is a colimit of ''F''. A '''cocontinuous functor''' is one that preserves all ''small'' colimits. | |||
If ''C'' is a [[complete category]], then, by the above existence theorem for limits, a functor ''G'' : ''C'' → ''D'' is continuous if and only if it preserves (small) products and equalizers. Dually, ''G'' is cocontinuous if and only if it preserves (small) coproducts and coequalizers. | |||
An important property of [[adjoint functors]] is that every right adjoint functor is continuous and every left adjoint functor is cocontinuous. Since adjoint functors exist in abundance, this gives numerous examples of continuous and cocontinuous functors. | |||
For a given diagram ''F'' : ''J'' → ''C'' and functor ''G'' : ''C'' → ''D'', if both ''F'' and ''GF'' have specified limits there is a unique canonical morphism | |||
:τ<sub>''F''</sub> : ''G'' lim ''F'' → lim ''GF'' | |||
which respects the corresponding limit cones. The functor ''G'' preserves the limits of ''F'' if and only this map is an isomorphism. If the categories ''C'' and ''D'' have all limits of type ''J'' then lim is a functor and the morphisms τ<sub>''F''</sub> form the components of a [[natural transformation]] | |||
:τ : ''G'' lim → lim ''G''<sup>''J''</sup>. | |||
The functor ''G'' preserves all limits of type ''J'' if and only if τ is a natural isomorphism. In this sense, the functor ''G'' can be said to ''commute with limits'' ([[up to]] a canonical natural isomorphism). | |||
Preservation of limits and colimits is a concept that only applies to ''[[covariant functor|covariant]]'' functors. For [[contravariant functor]]s the corresponding notions would be a functor that takes colimits to limits, or one that takes limits to colimits. | |||
===Lifting of limits=== | |||
A functor ''G'' : ''C'' → ''D'' is said to '''lift limits''' for a diagram ''F'' : ''J'' → ''C'' if whenever (''L'', φ) is a limit of ''GF'' there exists a limit (''L''′, φ′) of ''F'' such that ''G''(''L''′, φ′) = (''L'', φ). A functor ''G'' '''lifts limits of type ''J''''' if it lifts limits for all diagrams of type ''J''. One can therefore talk about lifting products, equalizers, pullbacks, etc. Finally, one says that ''G'' '''lifts limits''' if it lifts all limits. There are dual definitions for the lifting of colimits. | |||
A functor ''G'' '''lifts limits uniquely''' for a diagram ''F'' if there is a unique preimage cone (''L''′, φ′) such that (''L''′, φ′) is a limit of ''F'' and ''G''(''L''′, φ′) = (''L'', φ). One can show that ''G'' lifts limits uniquely if and only if it lifts limits and is [[amnestic functor|amnestic]]. | |||
Lifting of limits is clearly related to preservation of limits. If ''G'' lifts limits for a diagram ''F'' and ''GF'' has a limit, then ''F'' also has a limit and ''G'' preserves the limits of ''F''. It follows that: | |||
*If ''G'' lifts limits of all type ''J'' and ''D'' has all limits of type ''J'', then ''C'' also has all limits of type ''J'' and ''G'' preserves these limits. | |||
*If ''G'' lifts all small limits and ''D'' is complete, then ''C'' is also complete and ''G'' is continuous. | |||
The dual statements for colimits are equally valid. | |||
===Creation and reflection of limits=== | |||
Let ''F'' : ''J'' → ''C'' be a diagram. A functor ''G'' : ''C'' → ''D'' is said to | |||
*'''create limits''' for ''F'' if whenever (''L'', φ) is a limit of ''GF'' there exists a unique cone (''L''′, φ′) to ''F'' such that ''G''(''L''′, φ′) = (''L'', φ), and furthermore, this cone is a limit of ''F''. | |||
*'''reflect limits''' for ''F'' if each cone to ''F'' whose image under ''G'' is a limit of ''GF'' is already a limit of ''F''. | |||
Dually, one can define creation and reflection of colimits. | |||
The following statements are easily seen to be equivalent: | |||
*The functor ''G'' creates limits. | |||
*The functor ''G'' lifts limits uniquely and reflects limits. | |||
There are examples of functors which lift limits uniquely but neither create nor reflect them. | |||
===Examples=== | |||
* For any category ''C'' and object ''A'' of ''C'' the covariant [[Hom functor]] Hom(''A'',–) : ''C'' → '''Set''' preserves all limits in ''C''. In particular, Hom functors are continuous. Hom functors need not preserve colimits. | |||
* Every [[representable functor]] ''C'' → '''Set''' preserves limits (but not necessarily colimits). | |||
* The [[forgetful functor]] ''U'' : '''Grp''' → '''Set''' creates (and preserves) all small limits and [[filtered colimit]]s; however, ''U'' does not preserve coproducts. This situation is typical of algebraic forgetful functors. | |||
* The [[free functor]] ''F'' : '''Set''' → '''Grp''' (which assigns to every set ''S'' the [[free group]] over ''S'') is left adjoint to forgetful functor ''U'' and is, therefore, cocontinuous. This explains why the [[free product]] of two free groups ''G'' and ''H'' is the free group generated by the [[disjoint union]] of the generators of ''G'' and ''H''. | |||
* The inclusion functor '''Ab''' → '''Grp''' creates limits but does not preserve coproducts (the coproduct of two abelian groups being the [[Direct sum of abelian groups|direct sum]]). | |||
* The forgetful functor '''Top''' → '''Set''' lifts limits and colimits uniquely but creates neither. | |||
* Let '''Met'''<sub>''c''</sub> be the category of [[metric space]]s with [[continuous function]]s for morphisms. The forgetful functor '''Met'''<sub>''c''</sub> → '''Set''' lifts finite limits but does not lift them uniquely. | |||
== A note on terminology == | |||
Older terminology referred to limits as "inverse limits" or "projective limits," and to colimits as "direct limits" or "inductive limits." This has been the source of a lot of confusion. | |||
There are several ways to remember the modern terminology. First of all, | |||
*cokernels, | |||
*coproducts, | |||
*coequalizers, and | |||
*codomains | |||
are types of colimits, whereas | |||
*kernels, | |||
*products | |||
*equalizers, and | |||
*domains | |||
are types of limits. Second, the prefix "co" implies "first variable of the <math>\operatorname{Hom}</math>". Terms like "cohomology" and "cofibration" all have a slightly stronger association with the first variable, i.e., the contravariant variable, of the <math>\operatorname{Hom}</math> bifunctor. | |||
== References == | |||
*{{cite book | last = Adámek | first = Jiří | coauthors = Horst Herrlich, and George E. Strecker | year = 1990 | url = http://katmat.math.uni-bremen.de/acc/acc.pdf | title = Abstract and Concrete Categories|publisher = John Wiley & Sons | isbn = 0-471-60922-6}} | |||
*{{cite book | first = Saunders | last = Mac Lane | authorlink = Saunders Mac Lane | year = 1998 | title = [[Categories for the Working Mathematician]] | series = [[Graduate Texts in Mathematics]] | volume=5 | edition = 2nd | publisher = [[Springer-Verlag]] | isbn = 0-387-98403-8 | zbl=0906.18001 }} | |||
== External links == | |||
*[http://www.j-paine.org/cgi-bin/webcats/webcats.php Interactive Web page ] which generates examples of limits and colimits in the category of finite sets. Written by [http://www.j-paine.org/ Jocelyn Paine]. | |||
[[Category:Limits (category theory)| ]] | |||
Revision as of 16:33, 14 December 2013
Template:More footnotes In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products, pullbacks and inverse limits. The dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushouts and direct limits.
Limits and colimits, like the strongly related notions of universal properties and adjoint functors, exist at a high level of abstraction. In order to understand them, it is helpful to first study the specific examples these concepts are meant to generalize.
Definition
Limits and colimits in a category C are defined by means of diagrams in C. Formally, a diagram of type J in C is a functor from J to C:
- F : J → C.
The category J is thought of as index category, and the diagram F is thought of as indexing a collection of objects and morphisms in C patterned on J. The actual objects and morphisms in J are largely irrelevant—only the way in which they are interrelated matters.
One is most often interested in the case where the category J is a small or even finite category. A diagram is said to be small or finite whenever J is.
Limits
Let F : J → C be a diagram of type J in a category C. A cone to F is an object N of C together with a family ψX : N → F(X) of morphisms indexed by the objects X of J, such that for every morphism f : X → Y in J, we have F(f) o ψX = ψY.
A limit of the diagram F : J → C is a cone (L, φ) to F such that for any other cone (N, ψ) to F there exists a unique morphism u : N → L such that φX o u = ψX for all X in J.
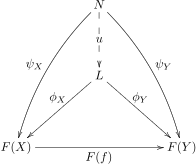
One says that the cone (N, ψ) factors through the cone (L, φ) with the unique factorization u. The morphism u is sometimes called the mediating morphism.
Limits are also referred to as universal cones, since they are characterized by a universal property (see below for more information). As with every universal property, the above definition describes a balanced state of generality: The limit object L has to be general enough to allow any other cone to factor through it; on the other hand, L has to be sufficiently specific, so that only one such factorization is possible for every cone.
Limits may also be characterized as terminal objects in the category of cones to F.
It is possible that a diagram does not have a limit at all. However, if a diagram does have a limit then this limit is essentially unique: it is unique up to a unique isomorphism. For this reason one often speaks of the limit of F.
Colimits
The dual notions of limits and cones are colimits and co-cones. Although it is straightforward to obtain the definitions of these by inverting all morphisms in the above definitions, we will explicitly state them here:
A co-cone of a diagram F : J → C is an object N of C together with a family of morphisms
- ψX : F(X) → N
for every object X of J, such that for every morphism f : X → Y in J, we have ψY o F(f)= ψX.
A colimit of a diagram F : J → C is a co-cone (L, ) of F such that for any other co-cone (N, ψ) of F there exists a unique morphism u : L → N such that u o X = ψX for all X in J.

Colimits are also referred to as universal co-cones. They can be characterized as initial objects in the category of co-cones from F.
As with limits, if a diagram F has a colimit then this colimit is unique up to a unique isomorphism.
Variations
Limits and colimits can also be defined for collections of objects and morphisms without the use of diagrams. The definitions are the same (note that in definitions above we never needed to use composition of morphisms in J). This variation, however, adds no new information. Any collection of objects and morphisms defines a (possibly large) directed graph G. If we let J be the free category generated by G, there is a universal diagram F : J → C whose image contains G. The limit (or colimit) of this diagram is the same as the limit (or colimit) of the original collection of objects and morphisms.
Weak limit and weak colimits are defined like limits and colimits, except that the uniqueness property of the mediating morphism is dropped.
Examples
Limits
The definition of limits is general enough to subsume several constructions useful in practical settings. In the following we will consider the limit (L, φ) of a diagram F : J → C.
- Terminal objects. If J is the empty category there is only one diagram of type J: the empty one (similar to the empty function in set theory). A cone to the empty diagram is essentially just an object of C. The limit of F is any object that is uniquely factored through by every other object. This is just the definition of a terminal object.
- Products. If J is a discrete category then a diagram F is essentially nothing but a family of objects of C, indexed by J. The limit L of F is called the product of these objects. The cone φ consists of a family of morphisms φX : L → F(X) called the projections of the product. In the category of sets, for instance, the products are given by Cartesian products and the projections are just the natural projections onto the various factors.
- Powers. A special case of a product is when the diagram F is a constant functor to an object X of C. The limit of this diagram is called the Jth power of X and denoted XJ.
- Equalizers. If J is a category with two objects and two parallel morphisms from object 1 to object 2 then a diagram of type J is a pair of parallel morphisms in C. The limit L of such a diagram is called an equalizer of those morphisms.
- Kernels. A kernel is a special case of an equalizer where one of the morphisms is a zero morphism.
- Pullbacks. Let F be a diagram that picks out three objects X, Y, and Z in C, where the only non-identity morphisms are f : X → Z and g : Y → Z. The limit L of F is called a pullback or a fiber product. It can nicely be visualized as a commutative square:

- Inverse limits. Let J be a directed poset (considered as a small category by adding arrows i → j if and only if i ≤ j) and let F : Jop → C be a diagram. The limit of F is called (confusingly) an inverse limit, projective limit, or directed limit.
- If J = 1, the category with a single object and morphism, then a diagram of type J is essentially just an object X of C. A cone to an object X is just a morphism with codomain X. A morphism f : Y → X is a limit of the diagram X if and only if f is an isomorphism. More generally, if J is any category with an initial object i, then any diagram of type J has a limit, namely any object isomorphic to F(i). Such an isomorphism uniquely determines a universal cone to F.
- Topological limits. Limits of functions are a special case of limits of filters, which are related to categorical limits as follows. Given a topological space X, denote F the set of filters on X, x ∈ X a point, V(x) ∈ F the neighborhood filter of x, A ∈ F a particular filter and the set of filters finer than A and that converge to x. The filters F are given a small and thin category structure by adding an arrow A → B if and only if A ⊆ B. The injection becomes a functor and the following equivalence holds :
Colimits
Examples of colimits are given by the dual versions of the examples above:
- Initial objects are colimits of empty diagrams.
- Coproducts are colimits of diagrams indexed by discrete categories.
- Copowers are colimits of constant diagrams from discrete categories.
- Coequalizers are colimits of a parallel pair of morphisms.
- Cokernels are coequalizers of a morphism and a parallel zero morphism.
- Pushouts are colimits of a pair of morphisms with common domain.
- Direct limits are colimits of diagrams indexed by directed sets.
Properties
Existence of limits
A given diagram F : J → C may or may not have a limit (or colimit) in C. Indeed, there may not even be a cone to F, let alone a universal cone.
A category C is said to have limits of type J if every diagram of type J has a limit in C. Specifically, a category C is said to
- have products if it has limits of type J for every small discrete category J (it need not have large products),
- have equalizers if it has limits of type (i.e. every parallel pair of morphisms has an equalizer),
- have pullbacks if it has limits of type (i.e. every pair of morphisms with common codomain has a pullback).
A complete category is a category that has all small limits (i.e. all limits of type J for every small category J).
One can also make the dual definitions. A category has colimits of type J if every diagram of type J has a colimit in C. A cocomplete category is one that has all small colimits.
The existence theorem for limits states that if a category C has equalizers and all products indexed by the classes Ob(J) and Hom(J), then C has all limits of type J. In this case, the limit of a diagram F : J → C can be constructed as the equalizer of the two morphisms
given (in component form) by
There is a dual existence theorem for colimits in terms of coequalizers and coproducts. Both of these theorems give sufficient but not necessary conditions for the existence of all (co)limits of type J.
Universal property
Limits and colimits are important special cases of universal constructions. Let C be a category and let J be a small index category. The functor category CJ may be thought of the category of all diagrams of type J in C. The diagonal functor
is the functor that maps each object N in C to the constant functor Δ(N) : J → C to N. That is, Δ(N)(X) = N for each object X in J and Δ(N)(f) = idN for each morphism f in J.
Given a diagram F: J → C (thought of as an object in CJ), a natural transformation ψ : Δ(N) → F (which is just a morphism in the category CJ) is the same thing as a cone from N to F. The components of ψ are the morphisms ψX : N → F(X). Dually, a natural transformation ψ : F → Δ(N) is the same thing as a co-cone from F to N.
The definitions of limits and colimits can then be restated in the form:
- A limit of F is a universal morphism from Δ to F.
- A colimit of F is a universal morphism from F to Δ.
Adjunctions
Like all universal constructions, the formation of limits and colimits is functorial in nature. In other words, if every diagram of type J has a limit in C (for J small) there exists a limit functor
which assigns each diagram its limit and each natural transformation η : F → G the unique morphism lim η : lim F → lim G commuting with the corresponding universal cones. This functor is right adjoint to the diagonal functor Δ : C → CJ. This adjunction gives a bijection between the set of all morphisms from N to lim F and the set of all cones from N to F
which is natural in the variables N and F. The counit of this adjunction is simply the universal cone from lim F to F. If the index category J is connected (and nonempty) then the unit of the adjunction is an isomorphism so that lim is a left inverse of Δ. This fails if J is not connected. For example, if J is a discrete category, the components of the unit are the diagonal morphisms δ : N → NJ.
Dually, if every diagram of type J has a colimit in C (for J small) there exists a colimit functor
which assigns each diagram its colimit. This functor is left adjoint to the diagonal functor Δ : C → CJ, and one has a natural isomorphism
The unit of this adjunction is the universal cocone from F to colim F. If J is connected (and nonempty) then the counit is an isomorphism, so that colim is a left inverse of Δ.
Note that both the limit and the colimit functors are covariant functors.
As representations of functors
One can use Hom functors to relate limits and colimits in a category C to limits in Set, the category of sets. This follows, in part, from the fact the covariant Hom functor Hom(N, –) : C → Set preserves all limits in C. By duality, the contravariant Hom functor must take colimits to limits.
If a diagram F : J → C has a limit in C, denoted by lim F, there is a canonical isomorphism
which is natural in the variable N. Here the functor Hom(N, F–) is the composition of the Hom functor Hom(N, –) with F. This isomorphism is the unique one which respects the limiting cones.
One can use the above relationship to define the limit of F in C. The first step is to observe that the limit of the functor Hom(N, F–) can be identified with the set of all cones from N to F:
The limiting cone is given by the family of maps πX : Cone(N, F) → Hom(N, FX) where πX(ψ) = ψX. If one is given an object L of C together with a natural isomorphism Φ : Hom(–, L) → Cone(–, F), the object L will be a limit of F with the limiting cone given by ΦL(idL). In fancy language, this amounts to saying that a limit of F is a representation of the functor Cone(–, F) : C → Set.
Dually, if a diagram F : J → C has a colimit in C, denoted colim F, there is a unique canonical isomorphism
which is natural in the variable N and respects the colimiting cones. Identifying the limit of Hom(F–, N) with the set Cocone(F, N), this relationship can be used to define the colimit of the diagram F as a representation of the functor Cocone(F, –).
Interchange of limits and colimits of sets
Let I be a finite category and J be a small filtered category. For any bifunctor
- F : I × J → Set
there is a natural isomorphism
In words, filtered colimits in Set commute with finite limits.
Functors and limits
If F : J → C is a diagram in C and G : C → D is a functor then by composition (recall that a diagram is just a functor) one obtains a diagram GF : J → D. A natural question is then:
- “How are the limits of GF related to those of F?”
Preservation of limits
A functor G : C → D induces a map from Cone(F) to Cone(GF): if Ψ is a cone from N to F then GΨ is a cone from GN to GF. The functor G is said to preserve the limits of F if (GL, Gφ) is a limit of GF whenever (L, φ) is a limit of F. (Note that if the limit of F does not exist, then G vacuously preserves the limits of F.)
A functor G is said to preserve all limits of type J if it preserves the limits of all diagrams F : J → C. For example, one can say that G preserves products, equalizers, pullbacks, etc. A continuous functor is one that preserves all small limits.
One can make analogous definitions for colimits. For instance, a functor G preserves the colimits of F if G(L, φ) is a colimit of GF whenever (L, φ) is a colimit of F. A cocontinuous functor is one that preserves all small colimits.
If C is a complete category, then, by the above existence theorem for limits, a functor G : C → D is continuous if and only if it preserves (small) products and equalizers. Dually, G is cocontinuous if and only if it preserves (small) coproducts and coequalizers.
An important property of adjoint functors is that every right adjoint functor is continuous and every left adjoint functor is cocontinuous. Since adjoint functors exist in abundance, this gives numerous examples of continuous and cocontinuous functors.
For a given diagram F : J → C and functor G : C → D, if both F and GF have specified limits there is a unique canonical morphism
- τF : G lim F → lim GF
which respects the corresponding limit cones. The functor G preserves the limits of F if and only this map is an isomorphism. If the categories C and D have all limits of type J then lim is a functor and the morphisms τF form the components of a natural transformation
- τ : G lim → lim GJ.
The functor G preserves all limits of type J if and only if τ is a natural isomorphism. In this sense, the functor G can be said to commute with limits (up to a canonical natural isomorphism).
Preservation of limits and colimits is a concept that only applies to covariant functors. For contravariant functors the corresponding notions would be a functor that takes colimits to limits, or one that takes limits to colimits.
Lifting of limits
A functor G : C → D is said to lift limits for a diagram F : J → C if whenever (L, φ) is a limit of GF there exists a limit (L′, φ′) of F such that G(L′, φ′) = (L, φ). A functor G lifts limits of type J if it lifts limits for all diagrams of type J. One can therefore talk about lifting products, equalizers, pullbacks, etc. Finally, one says that G lifts limits if it lifts all limits. There are dual definitions for the lifting of colimits.
A functor G lifts limits uniquely for a diagram F if there is a unique preimage cone (L′, φ′) such that (L′, φ′) is a limit of F and G(L′, φ′) = (L, φ). One can show that G lifts limits uniquely if and only if it lifts limits and is amnestic.
Lifting of limits is clearly related to preservation of limits. If G lifts limits for a diagram F and GF has a limit, then F also has a limit and G preserves the limits of F. It follows that:
- If G lifts limits of all type J and D has all limits of type J, then C also has all limits of type J and G preserves these limits.
- If G lifts all small limits and D is complete, then C is also complete and G is continuous.
The dual statements for colimits are equally valid.
Creation and reflection of limits
Let F : J → C be a diagram. A functor G : C → D is said to
- create limits for F if whenever (L, φ) is a limit of GF there exists a unique cone (L′, φ′) to F such that G(L′, φ′) = (L, φ), and furthermore, this cone is a limit of F.
- reflect limits for F if each cone to F whose image under G is a limit of GF is already a limit of F.
Dually, one can define creation and reflection of colimits.
The following statements are easily seen to be equivalent:
- The functor G creates limits.
- The functor G lifts limits uniquely and reflects limits.
There are examples of functors which lift limits uniquely but neither create nor reflect them.
Examples
- For any category C and object A of C the covariant Hom functor Hom(A,–) : C → Set preserves all limits in C. In particular, Hom functors are continuous. Hom functors need not preserve colimits.
- Every representable functor C → Set preserves limits (but not necessarily colimits).
- The forgetful functor U : Grp → Set creates (and preserves) all small limits and filtered colimits; however, U does not preserve coproducts. This situation is typical of algebraic forgetful functors.
- The free functor F : Set → Grp (which assigns to every set S the free group over S) is left adjoint to forgetful functor U and is, therefore, cocontinuous. This explains why the free product of two free groups G and H is the free group generated by the disjoint union of the generators of G and H.
- The inclusion functor Ab → Grp creates limits but does not preserve coproducts (the coproduct of two abelian groups being the direct sum).
- The forgetful functor Top → Set lifts limits and colimits uniquely but creates neither.
- Let Metc be the category of metric spaces with continuous functions for morphisms. The forgetful functor Metc → Set lifts finite limits but does not lift them uniquely.
A note on terminology
Older terminology referred to limits as "inverse limits" or "projective limits," and to colimits as "direct limits" or "inductive limits." This has been the source of a lot of confusion.
There are several ways to remember the modern terminology. First of all,
- cokernels,
- coproducts,
- coequalizers, and
- codomains
are types of colimits, whereas
- kernels,
- products
- equalizers, and
- domains
are types of limits. Second, the prefix "co" implies "first variable of the ". Terms like "cohomology" and "cofibration" all have a slightly stronger association with the first variable, i.e., the contravariant variable, of the bifunctor.
References
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
External links
- Interactive Web page which generates examples of limits and colimits in the category of finite sets. Written by Jocelyn Paine.

















