Recurrent tensor
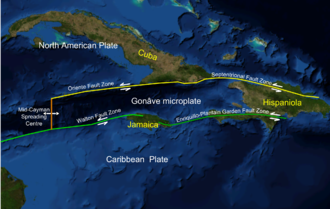
Cuba is located in an area with several active fault systems which produce on average about 2000 seismic events each year.[1] While most registered seismic events pass unnoticed, the island has been struck by a number of destructive earthquakes over the past four centuries, including several major quakes with a magnitude of 7.0 or above.
Approximately 70% of seismic activity in Cuba emanates from the Oriente fault zone, located in the Bartlett-Cayman fault system which runs along the south-eastern coast of Cuba and marks the tectonic boundary between the North American Plate and the Caribbean Plate.[2] The 12 currently active faults in Cuba also include the Cauto-Nipe, Cochinos and Nortecubana faults.[2] Destructive earthquakes originating from the Oriente fault occurred in 1766 (=7.6), 1852 (=7.2) and 1932 (=6.75).[3] Some studies suggest there is a high probability the Oriente fault will produce a magnitude 7 earthquake in the near future.[4]
List of earthquakes in Cuba
Earlier than you decide whether or not chrome steel cookware is value buying, lets first focus on what chrome steel cookware is. Chrome steel is manufactured from an alloy, or a mix of metals. Mostly, primary iron with chromium, nickel or another minor metals. The chromium supplies rust safety and gives your cookware durability. The nickel supplies rust safety as properly, and adds a polished look. Most nicely made chrome steel cookware has copper or aluminum added to the bottom of the pan or pot. That is completed to increases the power of the pot or pan to conduct warmth.
The most effective chrome steel cookware is the primary category, but nonetheless it's divided into a number of subcategories based mostly on the quality and the price range. It may be complicated to choose the most effective stainless steel cookware out of the classes that can meet your necessities. That is where we took a step forward to clarify you all the information that will likely be useful so that you can know how to decide on the most effective chrome steel cookware. The perfect stainless-steel cookware set is manufactured from cheap to costly and high quality constructed pots and pans.
You will discover magnetic stainless steel in the layer on the skin of some high quality items of stainless-steel. This is to make it compatible with induction stovetops, which contain the use of a rapidly charging electromagnetic area to warmth cookware. Excessive-high quality stainless-steel, like All-Clad , uses three layers of metal—the austenite layer of steel on the inside, ferrite metal on the outside, and a layer of aluminum sandwiched between the 2 for optimal warmth conductivity (metal alone doesn't conduct heat evenly). Lesser-quality chrome steel is usually only one layer of austenitic chrome steel.
Aesthetically talking, stainless-steel is a smart alternative if you happen to prefer to show or hold pots or pans. The clear, crisp look of all stainless-steel kitchenware can transform a mishmash of cookware into a classy décor statement. Stainless steel kettles, such as the Cuisinart Tea Kettle will combine particular person kitchenware right into a cohesive and pleasant entity. Think about purchasing stainless-steel utensils as well. Already acquired a gorgeous stainless steel cookware assortment? The Cuisinart Chef’s Assortment stainless pot rack could be the final touch for a kitchen, liberating up area and making those pots and pans readily accessible. Get the chrome steel cookware of your culinary desires at Macy’s!
Exhausting-anodized aluminum cookware is one of the hottest varieties of material, regardless that many individuals do not quite perceive the development. Hard-anodized aluminum is obvious aluminum that has been processed in a series of chemical baths charged with an electrical present. The result's a fabric that has the identical superior warmth conductivity as aluminum however is non-reactive with acidic foods, resembling tomatoes, and twice as onerous as chrome steel. Two drawbacks to laborious-anodized cookware are that it's not dishwasher-protected and, as a result of it isn't magnetic, it is not going to work with induction vary tops.
The enamel over steel technique creates a chunk that has the warmth distribution of carbon steel and a non-reactive, low-stick surface. Such pots are a lot lighter than most other pots of comparable size, are cheaper to make than chrome steel pots, and should not have the rust and reactivity problems with cast iron or carbon metal. citation wanted Enamel over steel is right for large stockpots and for different giant pans used principally for water-based cooking. Due to its mild weight and straightforward cleanup, enamel over steel is also in style for cookware used while camping. Clad aluminium or copper edit
Unique specialty cookware pieces served a la carte to compliment any cookware set are constructed of a sturdy Stainless Metal with a brushed exterior end. Designed with an impression bonded, aluminum disk encapsulated base which distributes heat rapidly and evenly to permit exact temperature management. Handles are riveted for sturdiness and efficiency. The New Specialty Cookware is compatible for all range varieties together with induction. Along with the multi use perform, another unique function is backside to top interior volume markings in both quarts and metric measurement; and every bit comes with a tempered glass lid, oven safe to 350°F.
Whether or not you are a cooking enthusiasts, a professional chef or simply cooking for your family you already know the importance of getting a totally stocked kitchen. Not solely do you need the right ingredients, but you also need the fitting instruments to get the job done. In any sort of fundamental cooking coaching lesson, you will study that chrome steel is your new greatest buddy relating to kitchen cookware. What you will also learn is that quality cooking gear does not normally come at a discounted value. When you loved this information and you would like to receive details with regards to best stainless steel cookware i implore you to visit our own page. For this reason, it is important to take good care of your cookware! Listed here are some basics for chrome steel care.
To fight the uneven heating drawback, most stainless steel pans are laminations of aluminum or copper on the underside to spread the heat around, and stainless-steel inside the pan to provide a cooking floor that is impervious to no matter you would possibly put inside. In my experience, this chrome steel floor remains to be too sticky to fry on, and for those who ever burn it you get a permanent bother spot. But, typically a chrome steel cooking surface comes in handy when you may't use aluminum (see beneath) so I preserve some around. Select something with a fairly thick aluminum layer on the underside.
Nicely, unless you’re a metals skilled and go examine the manufacturing unit where the steel is made to see whether or not their manufacturing process creates a pure austenite without corrosive materials shaped, you’re not going to know for certain whether or not or not the craftsmanship of your stainless is of the very best high quality. I feel your best wager is to simply buy high-high quality stainless-steel from the beginning, from a model with a reputation for good quality. But, I believe I've found out a method that you can decide if the stainless cookware you have already got is potentially reactive.
Notable earthquakes in recent Cuban history include the following:
| Name | Date | Epicentre | M | Intensity | Depth | Notes | Deaths |
|---|---|---|---|---|---|---|---|
| 1578 Cuba earthquake | August 1578 |
Santiago de Cuba[1] | 6.8 | VIII | 30 km | Magnitude estimated at 6.8 ML on the Richter scale, intensity at VIII EMS-98.[1] | |
| 1580 Cuba earthquake | 1580-12-19 |
Santiago de Cuba [5] | |||||
| 1632 Cuba earthquake | October 1632 |
Santiago de Cuba [6] | |||||
| 1675 Cuba earthquake | 1675-02-11 |
Santiago de Cuba [1][7] | 5.8 | VII | 30 km | Magnitude estimated at 5.8 ML on the Richter scale, intensity at VII EMS-98.[1] | |
| 1678 Cuba earthquake | 1678-02-11 14:59 |
Santiago de Cuba [7] | 6.8 | VIII | 30 km | Magnitude estimated at 6.8 ML on the Richter scale, intensity at VIII EMS-98.[1] | |
| 1679 Cuba earthquake | 1679-02-11 |
Santiago de Cuba [7] | |||||
| 1682 Cuba earthquake | 1682 |
Santiago de Cuba [7] | 5.8 | VII | 30 km | Magnitude estimated at 5.8 ML on the Richter scale, intensity at VII EMS-98.[1] | |
| 1693 Cuba earthquake | July 1693 |
Havana[8] | "1,500 houses thrown down" | ||||
| 1757 Cuba earthquake | 1757-12-14 |
Santiago de Cuba [9] | |||||
| 1766 Cuba earthquake | 1766-06-11 05:14 |
Santiago de Cuba [10] | 7.6 [3] | IX | 35 km | Magnitude estimated at 7.6 ML on the Richter scale, intensity at IX EMS-98.[1] | 120 |
| 1826 Cuba earthquake | 1826-09-18 09:26 |
Santiago de Cuba [11] | 5.8 | VII | 30 km | Magnitude estimated at 5.8 ML on the Richter scale, intensity at VII EMS-98.[1] | |
| 1842 Cuba earthquake | 1842-07-07 |
Santiago de Cuba[1] | 6.0 | VII | 30 km | Magnitude estimated at 6.0 ML on the Richter scale, intensity at VII EMS-98.[1] | |
| 1852 Cuba earthquake | 1852-08-20 14:05 UTC |
Santiago de Cuba [10][12] | 7.2 [3] | IX | 30 km | Magnitude intensity estimated at IX EMS-98,[1] with 26 heavy aftershocks. Caused severe damage to Churches and other buildings in Santiago de Cuba, as well as landslides in the Sierra Maestra region. Shaking felt in the whole of eastern Cuba, up to the islands of Jamaica and Hispaniola.[13] | |
| 1852 Cuba earthquake (November) | 1852-11-26 08:37 GMT |
Santiago de Cuba, Sierra Maestra[1][14] | 7.0 | VIII | 35 km | ||
| 1858 Cuba earthquake | 1858-01-28 22:04 |
Santiago de Cuba[1] | 6.5 | VII | 30 km | ||
| 1880 Cuba earthquake | 1880-01-23 04:39 |
San Cristóbal/Vuelta Abajo (Pinar del Río) [1][15][16] | 6.0 | VIII | 15 km | A series of severe shock waves originating from western Cuba were also felt in the town of Key West (Florida), and included a strong earthquake on 23 January 1880 in San Cristóbal, Pinar del Río at 4 a.m.[16] | |
| 1903 Cuba earthquake | 1903-09-22 08:09 |
Santiago de Cuba[1] | 5.7 | VII | 30 km | ||
| 1906 Cuba earthquake | 1906-06-22 07:09 |
Santiago de Cuba[1] | 6.2 | VII | 30 km | ||
| 1914 Cuba earthquake | 1914-02-28 05:19 |
Gibara[1] | 6.2 | VII | 32 km | ||
| 1914 Cuba earthquake | 1914-12-25 05:19 |
Santiago de Cuba[1] | 6.7 | VII | 30 km | ||
| 1932 Cuba earthquake | 1932-02-03 |
Template:Coord Santiago de Cuba [17] |
6.75 [3] | VIII | Intensity estimated at VIII EMS-98.[1] 8[17] - 1500[18] deaths, 300 injured. 80% of buildings in Santiago de Cuba affected.,[17] with damages totaling 15 million Pesos.[13] | 8 | |
| 1947 Cuba earthquake | 1947-08-07 00:40:20 hrs |
Template:Coord |
6.8 | VIII | 50 km | Magnitude estimated at 6.8 ML and intensity VIII EMS-98.[1] | |
| 1992 Cuba earthquake | 1992-05-25 16:55:04 UTC |
Template:Coord Cabo Cruz, Pilón–Manzanillo[20] |
6.9 [21] | VII | 23 km | A strong earthquake struck the Cabo Cruz sector, leaving 40 people injured and more than 820 buildings damaged in the Pilon-Manzanillo area.[22] | |
| 2010 Cuba earthquake | 2010-03-20 18:08:09 UTC |
Template:Coord Offshore Oriente Fault, 50 km SSW of Guantanamo [23] |
5.6 | V | 16.7 km | According to USGS: "Felt (V) at Baracoa, Guantanamo and Santiago de Cuba, (III) at Camagüey and (II) at Havana. Also felt at Banes, Bayamo and Pinar del Río. Felt (II) at Half Way Tree and Mona, Jamaica. Felt in Jamaica and in parts of The Bahamas, Dominican Republic and Haiti".[23] The quake was followed by a 4.8 aftershock, 19:31:29 UTC of the same day. There were no reports of damages or casualties. | - |
Intensity= Intensity on the European Macroseismic Scale (EMS-98), which is somewhat similar to the Modified Mercalli scale (MM)
See also
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
Other sources
- Template:Cite web
- One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - Template:Cite web
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19 1.20 Oficina Nacional de Estadísticas, 2009
- ↑ 2.0 2.1 Cotilla, 2007
- ↑ 3.0 3.1 3.2 3.3 Alvarez 1999:2
- ↑ Rubio, 1985
- ↑ Milne, 1912: 30
- ↑ Milne, 1912: 32
- ↑ 7.0 7.1 7.2 7.3 Milne, 1912: 36
- ↑ Milne, 1912: 37
- ↑ Milne, 1912: 44
- ↑ 10.0 10.1 Cotilla, 2003 Cite error: Invalid
<ref>tag; name "Cotilla2003" defined multiple times with different content - ↑ Milne, 1912: 54
- ↑ Milne, 1912: 62
- ↑ 13.0 13.1 ONE, 2006
- ↑ Milne 1912: 63
- ↑ Milne 1912: 80
- ↑ 16.0 16.1 Template:Cite web
- ↑ 17.0 17.1 17.2 Template:Cite web
- ↑ Earthquake in Cuba. 1500 Deaths reported. The Sidney Morning Herald, Feb. 4, 1932.
- ↑ A Chronological History of the U.S. Navy Cruiser U.S.S. LITTLE ROCK
- ↑ Template:Cite web
- ↑ Pierrot et al, 1998
- ↑ Earthquake in Cuba Injures 40 and Destroys 100 Homes
- ↑ 23.0 23.1 Template:Cite web Template:Dead link