Yen's algorithm

Geoneutrino is an electron antineutrino emitted in [[Beta decay|Template:SubatomicParticle decay]] of a radionuclide naturally occurring in the Earth. Neutrinos, the lightest of the known subatomic particles, lack measurable electromagnetic properties and interact only via the weak nuclear force. Matter is virtually transparent to neutrinos and consequently they travel, unimpeded, at near light speed through the Earth from their point of emission. Collectively, geoneutrinos carry integrated information about the abundances of their radioactive sources inside the Earth. A major objective of the emerging field of neutrino geophysics involves extracting geologically useful information (e.g., abundances of individual geoneutrino-producing elements and their spatial distribution in Earth’s interior) from geoneutrino measurements.

Most geoneutrinos originate from Template:SubatomicParticle decay-branches of ⁴⁰K, ²³²Th and ²³⁸U. Together these decay chains account for more than 99% of the present-day radiogenic heat generated inside the Earth. Only geoneutrinos from ²³²Th and ²³⁸U decay chains are detectable by the inverse beta-decay mechanism because these have energies above the corresponding threshold (1.8 MeV). In neutrino experiments, large underground liquid scintillator detectors record the flashes of light generated from this interaction. Template:As of geoneutrino measurements at two sites, as reported by the KamLAND and Borexino collaborations, have begun to place constraints on the amount of radiogenic heating in the Earth's interior. A third detector (SNO+) is expected to start collecting data in 2013. A number of future geoneutrino detectors are being planned.

History

[[File:Beta Negative Decay.svg|thumb|The Feynman diagram for [[Beta decay|Template:SubatomicParticle decay]] of a neutron into a proton, electron, and electron antineutrino via an intermediate [[W boson|Template:SubatomicParticle boson]].]] Neutrinos were hypothesized in 1930 by Wolfgang Pauli. The first detection—of antineutrinos generated in a nuclear reactor—was confirmed in 1956. The idea of studying geologically produced neutrinos to infer Earth’s composition has been around since at least mid-1960s. In a 1984 landmark paper Krauss, Glashow & Schramm presented calculations of the predicted geoneutrino flux and discussed the possibilities for detection. First detection of geoneutrinos was reported in 2005 by the KamLAND experiment at the Kamioka Observatory in Japan. In 2010 the Borexino experiment at the Gran Sasso National Laboratory in Italy released their geoneutrino measurement. Updated results from KamLAND were published in 2011.

Geoneutrino science meetings

A number of scientific meetings focused on neutrino geophysics took place:

• Neutrino Sciences 2005, Neutrino Geophysics, Honolulu, Hawaii, 14–16 December 2005
• Union Session U41F – Geoneutrinos: A New Tool for the Study of the Solid Earth I, AGU 2006 Joint Assembly, Baltimore, Maryland, 23–26 May 2006 (session information)
• Neutrino Sciences 2007, Deep Ocean Anti-Neutrino Observatory Workshop, Honolulu, Hawaii, 23–25 March 2007
• Neutrino Geoscience 2008 at SNOLAB, Sudbury, Ontario, Canada, 17–19 September 2008
• Neutrino Geoscience 2010, Gran Sasso National Laboratory, Italy, 6–8 October 2010
• Neutrino Geoscience Workshop at CETUP* 2011, Deadwood, South Dakota, 20–22 June 2011
• Neutrino Geoscience 2013, Takayama, Japan, 21–23 March 2013 (planned)

Geophysical motivation

Geologically significant antineutrino- and heat-producing radioactive decays and decay chains

$\begin{array}{rcl}92238\text{U}& ⟶& 82206\text{Pb}+8\alpha +6e^{-}+6{\overline{\nu }}_e+51.698\text{MeV}\\ 92235\text{U}& ⟶& 82207\text{Pb}+7\alpha +4e^{-}+4{\overline{\nu }}_e+46.402\text{MeV}\\ 90232\text{Th}& ⟶& 82208\text{Pb}+6\alpha +4e^{-}+4{\overline{\nu }}_e+42.652\text{MeV}\\ 1940\text{K}& \stackrel{89.3\%}{⟶}& 2040\text{Ca}+e^{-}+{\overline{\nu }}_e+1.311\text{MeV}\\ 1940\text{K}+e^{-}& \stackrel{10.7\%}{⟶}& 1840\text{Ar}+{\nu }_e+1.505\text{MeV}\end{array}$

The Earth's interior radiates heat at a rate of about 47 TW (terawatts), which is less than 0.1% of the incoming solar energy. Part of this heat loss is accounted for by the heat generated upon decay of radioactive isotopes in the Earth interior. The remaining heat loss is due to the secular cooling of the Earth, growth of the Earth’s inner core (gravitational energy and latent heat contributions), and other processes. The most important heat-producing elements are uranium (U), thorium (Th), and potassium (K). The debate about their abundances in the Earth has not concluded. Various compositional estimates exist where the total Earth’s internal radiogenic heating rate ranges from as low at ~10 TW to as high as ~30 TW. About 7 TW worth of heat-producing elements reside in the Earth's crust, the remaining power is distributed in the Earth mantle; the amount of U, Th, and K in the Earth core is probably negligible. Radioactivity in the Earth mantle provides internal heating to power mantle convection, which is the driver of plate tectonics. The amount of mantle radioactivity and its spatial distribution—is the mantle compositionally uniform at large scale or composed of distinct reservoirs?—is of importance to geophysics.

The existing range of compositional estimates of the Earth reflects our lack of understanding of what were the processes and building blocks (chondritic meteorites) that contributed to its formation. More accurate knowledge of U, Th, and K abundances in the Earth interior would improve our understanding of present-day Earth dynamics and of Earth formation in early Solar System. Counting antineutrinos produced in the Earth can constrain the geological abundance models. The weakly interacting geoneutrinos carry information about their emitters’ abundances and location in the entire Earth volume, including the deep Earth. Extracting compositional information about the Earth mantle from geoneutrino measurements is difficult but possible. It requires a synthesis of geoneutrino experimental data with geochemical and geophysical models of the Earth. Existing geoneutrino data are a byproduct of antineutrino measurements with detectors designed primarily for fundamental neutrino physics research. Future experiments devised with a geophysical agenda in mind would benefit geoscience. Proposals for such detectors have been put forward.

Geoneutrino prediction

Geoneutrino signal prediction at Earth's surface in terrestrial neutrino units (TNU).

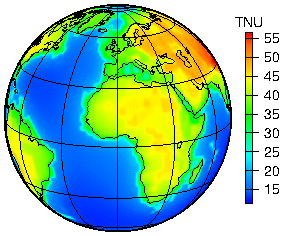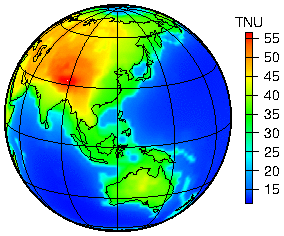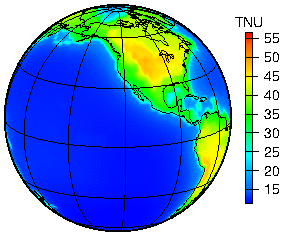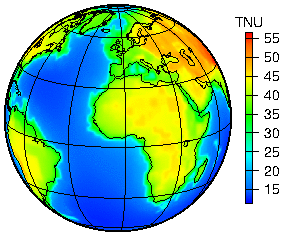
Calculations of the expected geoneutrino signal predicted for various Earth reference models are an essential aspect of neutrino geophysics. In this context, "Earth reference model" means the estimate of heat producing element (U, Th, K) abundances and assumptions about their spatial distribution in the Earth, and a model of Earth’s internal density structure. By far the largest variance exists in the abundance models where several estimates have been put forward. They predict a total radiogenic heat production as low as ~10 TW and as high as ~30 TW, the commonly employed value being around 20 TW. A density structure dependent only on the radius (such as the Preliminary Reference Earth Model or PREM) with a 3-D refinement for the emission from the Earth’s crust is generally sufficient for geoneutrino predictions.

The geoneutrino signal predictions are crucial for two main reasons: 1) they are used to interpret geoneutrino measurements and test the various proposed Earth compositional models; 2) they can motivate the design of new geoneutrino detectors. The typical geoneutrino flux at Earth's surface is few × 10⁶ cm⁻² s⁻¹. As a consequence of i) high enrichment of continental crust in heat producing elements (~7 TW of radiogenic power) and ii) the dependence of the flux on 1/(distance from point of emission)², the geoneutrino signal pattern correlates well with the distribution of continents. At continental sites, most geoneutrinos are produced locally in the crust. This calls for an accurate crustal model, both in terms of composition and density, a nontrivial task.

Antineutrino emission from a volume V is calculated for each radionuclide from the following equation:

$\frac{\mathrm{d}\varphi (E_{{\overline{\nu }}_e},\overrightarrow{r})}{\mathrm{d}{E}_{{\overline{\nu }}_e}}=10\frac{\lambda X{N}_A}{M}\frac{\mathrm{d}n(E_{{\overline{\nu }}_e})}{\mathrm{d}{E}_{{\overline{\nu }}_e}}\underset{V}{\int }{\mathrm{d}}^3{\overrightarrow{r}}^{\prime }\frac{A({\overrightarrow{r}}^{\prime })\rho ({\overrightarrow{r}}^{\prime })P_{ee}(E_{{\overline{\nu }}_e},|\overrightarrow{r}-{\overrightarrow{r}}^{\prime }|)}{4\pi |\overrightarrow{r}-{\overrightarrow{r}}^{\prime }{|}^2}$

where dφ(E_ν,r)/dE_ν is the fully oscillated antineutrino flux energy spectrum (in cm⁻² s⁻¹ MeV⁻¹) at position r (units of m) and E_ν is the antineutrino energy (in MeV). On the right-hand side, ρ is rock density (in kg m⁻³), A is elemental abundance (kg of element per kg of rock) and X is the natural isotopic fraction of the radionuclide (isotope/element), M is atomic mass (in g mol⁻¹), N_A is Avogadro's number (in mol⁻¹), λ is decay constant (in s⁻¹), dn(E_ν)/dE_ν is the antineutrino intensity energy spectrum (in MeV⁻¹, normalized to the number of antineutrinos n_ν produced in a decay chain when integrated over energy), and P_ee(E_ν,L) is the antineutrino survival probability after traveling a distance L. For an emission domain the size of the Earth, the fully oscillated energy-dependent survival probability P_ee can be replaced with a simple factor ⟨P_ee⟩≈0.55, the average survival probability. Integration over the energy yields the total antineutrino flux (in cm⁻² s⁻¹) from a given radionuclide:

$\varphi (\overrightarrow{r})=10\frac{n_{{\overline{\nu }}_e}⟨P_{ee}⟩\lambda X{N}_A}{M}\underset{V}{\int }{\mathrm{d}}^3{\overrightarrow{r}}^{\prime }\frac{A({\overrightarrow{r}}^{\prime })\rho ({\overrightarrow{r}}^{\prime })}{4\pi |\overrightarrow{r}-{\overrightarrow{r}}^{\prime }{|}^2}$

The total geoneutrino flux is the sum of contributions from all antineutrino-producing radionuclides. The geological inputs—the density and particularly the elemental abundances—carry a large uncertainty. The uncertainty of the remaining nuclear and particle physics parameters is negligible compared to the geological inputs.

Geoneutrino detection

Detection mechanism

Instruments that measure geoneutrinos are large-size scintillation detectors. They use the inverse beta decay reaction, a method proposed by Bruno Pontecorvo that Frederick Reines and Clyde Cowan employed in their pioneering experiments in 1950s. Inverse beta decay is a charged current weak interaction, where an electron antineutrino interacts with a proton, producing a positron and a neutron:

${\overline{\nu }}_e+p\to e^{+}+n$

Only antineutrinos with energies above the kinematic threshold of 1.804 MeV—the difference between rest mass energies of neutron plus positron and proton—can participate in this interaction. The positron promptly annihilates with an electron:

$e^{+}+e^{-}\to \gamma +\gamma$

With a delay of few tens to few hundred microseconds the neutron combines with a proton to form a deuteron:

$n+p\to d+\gamma$

The two light flashes associated with the positron annihilation and the deuteron formation are coincident in time and in space, which provides a powerful method to reject single-flash (non-antineutrino) background events in the liquid scintillator. Antineutrinos produced in man-made nuclear reactors overlap in energy range with geologically produced antineutrinos and are also counted by these detectors.

Because of the kinematic threshold of this antineutrino detection method, only the highest energy geoneutrinos from ²³²Th and ²³⁸U decay chains can be detected. Geoneutrinos from ⁴⁰K decay have energies below the threshold and cannot be detected using inverse beta decay reaction. Experimental particle physicists are developing other detection methods, which are not limited by an energy threshold (e.g., antineutrino scattering on electrons) and thus would allow detection of geoneutrinos from potassium decay.

Geoneutrino measurements are often reported in Terrestrial Neutrino Units (TNU; analogy with Solar Neutrino Units) rather than in units of flux (cm⁻² s⁻¹). TNU is specific to the inverse beta decay detection mechanism with protons. 1 TNU corresponds to 1 geoneutrino event recorded over a year-long fully efficient exposure of 10³² free protons, which is approximately the number of free protons in a 1 kiloton liquid scintillation detector. The conversion between flux units and TNU depends on the thorium to uranium abundance ratio (Th/U) of the emitter. For Th/U=4.0 (a typical value for the Earth), a flux of 1.0 × 10⁶ cm⁻² s⁻¹ corresponds to 8.9 TNU.

Detectors and results

Schematic of the KamLAND antineutrino detector.

Existing detectors

KamLAND (Kamioka Liquid Scintillator Antineutrino Detector) is a 1.0 kiloton detector located at the Kamioka Observatory in Japan. Results based on detector live-time of 749 days and presented in 2005 mark the first detection of geoneutrinos. The total number of detected antineutrino events was 152, of which geoneutrinos were 4.5 to 54.2 (90% confidence interval) with a central value of 28.0. This analysis put a 60 TW upper limit (99% confidence level) on the Earth’s radiogenic power from ²³²Th and ²³⁸U.

A 2011 update of KamLAND’s result used data from 2135 days of detector live-time and benefited from improved purity of the scintillator as well as a reduced reactor antineutrino background (21-month long shutdown of the Kashiwazaki-Kariwa nuclear power plant after the July 2007 Chūetsu earthquake). Of 841 candidate antineutrino events, 106 (+29/−28 asymmetric error) were identified as geoneutrino using unbinned maximum likelihood analysis with Th/U ratio fixed at 3.9. It was found that ²³²Th and ²⁸²U together generate 20.0 (+8.8/−8.6) TW of radiogenic power.

Borexino is a 0.3 kiloton detector at Laboratori Nazionali del Gran Sasso near L'Aquila, Italy. Results published in 2010 used data collected over live-time of 537 days. Of 15 candidate events, unbinned maximum likelihood analysis identified 9.9 (+4.1/−3.4) as geoneutrinos. Geoneutrino null hypothesis was rejected at 99.997% confidence level (4.2σ). The data also rejected a hypothesis of an active georeactor in the Earth’s core with power above 3 TW at 95% confidence level.

SNO+ is a 0.8 kiloton detector located at SNOLAB near Sudbury, Ontario, Canada. SNO+ uses the original SNO experiment chamber. The detector is currently being refurbished and is expected to become operational in 2013.

Planned and proposed detectors

• LENA (Low Energy Neutrino Astronomy, website) is a proposed 50 kiloton liquid scintillation detector of the LAGUNA project. Proposed sites include Centre for Underground Physics in Pyhäsalmi (CUPP), Finland (preferred) and Laboratoire Souterrain de Modane (LSM) in Fréjus, France.
• at DUSEL (Deep Underground Science and Engineering Laboratory) at Homestake in Lead, South Dakota, USA
• at BNO (Baksan Neutrino Observatory) in Russia
• at Daya Bay-II experiment in China
• EARTH (Earth AntineutRino TomograpHy)
• Hanohano (Hawaii Anti-Neutrino Observatory) is a proposed deep-ocean transportable detector. It is the only detector designed to operate away from the Earth's continental crust and from nuclear reactors in order to increase the sensitivity to geoneutrinos from the Earth's mantle.

Desired future technologies

• Directional antineutrino detection. Resolving the direction from which an antineutrino arrived would help discriminate between the crustal geoneutrino and reactor antineutrino signal (most antineutrinos arriving near horizontally) from mantle geoneutrinos (much wider range of incident dip angles).
• Detection of antineutrinos from ⁴⁰K decay. Since the energy spectrum of antineutrinos from ⁴⁰K decay falls entirely below the threshold energy of inverse beta decay reaction (1.8 MeV), a different detection mechanism must be exploited, such as antineutrino scattering on electrons.

References

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.

Further reading

• 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
  
  My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
• One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
  
  In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
  
  Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
  
  Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
  
  A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
  
  The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
  
  There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang