Reciprocal gamma function
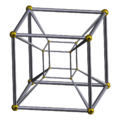 Tesseract Template:CDD |
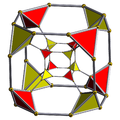 Truncated tesseract Template:CDD |
 Rectified tesseract Template:CDD |
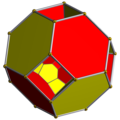 Bitruncated tesseract Template:CDD |
| Schlegel diagrams centered on [4,3] (cells visible at [3,3]) | |||
 16-cell Template:CDD |
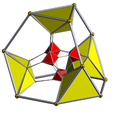 Truncated 16-cell Template:CDD |
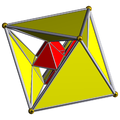 Rectified 16-cell (24-cell) Template:CDD |
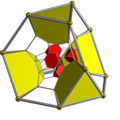 Bitruncated tesseract Template:CDD |
| Schlegel diagrams centered on [3,3] (cells visible at [4,3]) | |||
In geometry, a truncated tesseract is a uniform polychoron (4-dimensional uniform polytope) formed as the truncation of the regular tesseract.
There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 16-cell.
Truncated tesseract
| Truncated tesseract | ||
|---|---|---|
 Schlegel diagram (tetrahedron cells visible) | ||
| Type | Uniform polychoron | |
| Schläfli symbol | t{4,3,3} | |
| Coxeter-Dynkin diagrams | Template:CDD | |
| Cells | 24 | 8 3.8.8 16 3.3.3 |
| Faces | 88 | 64 {3} 24 {8} |
| Edges | 128 | |
| Vertices | 64 | |
| Vertex figure | 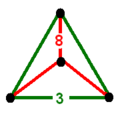 Isosceles triangular pyramid | |
| Dual | Tetrakis 16-cell | |
| Symmetry group | BC4, [4,3,3], order 384 | |
| Properties | convex | |
| Uniform index | 12 13 14 | |
The truncated tesseract is bounded by 24 cells: 8 truncated cubes, and 16 tetrahedra.
Alternate names
- Truncated tesseract (Norman W. Johnson)
- Truncated tesseract (Acronym tat) (George Olshevsky, and Jonathan Bowers)[1]
Construction
The truncated tesseract may be constructed by truncating the vertices of the tesseract at of the edge length. A regular tetrahedron is formed at each truncated vertex.
The Cartesian coordinates of the vertices of a truncated tesseract having edge length 2 is given by all permutations of:
Projections

In the truncated cube first parallel projection of the truncated tesseract into 3-dimensional space, the image is laid out as follows:
- The projection envelope is a cube.
- Two of the truncated cube cells project onto a truncated cube inscribed in the cubical envelope.
- The other 6 truncated cubes project onto the square faces of the envelope.
- The 8 tetrahedral volumes between the envelope and the triangular faces of the central truncated cube are the images of the 16 tetrahedra, a pair of cells to each image.
Images
Template:4-cube Coxeter plane graphs
 A polyhedral net |
 Truncated tesseract projected onto the 3-sphere with a stereographic projection into 3-space. |
Related polytopes
The truncated tesseract, is third in a sequence of truncated hypercubes:
I just lately had the opportunity to check a plugin referred to as the WooCommerce Reserving and Appointments Plugin from Tyche Softwares. It adds booking and appointment functionality to your WordPress powered web site, and integrates properly with WooCommerce to charge a price for these bookings.
So you possibly can see that with just some simple shortcodes, you may add advanced conduct to your Product element web page. What’s extra, using the Content Template Meta HTML, you can show and magnificence your merchandise to match your present theme. In our case, using the Toolset Bootstrap theme , with just a couple lessons, we’ve made our Product element page, absolutely responsive. Buy or select product for itemizing pages – Displays add to cart button for the easy product. For Variable products shows ‘Choose choices’ button which takes the customer to the detail page.
RENO is multipurpose WordPress WooCommerce theme suitable for corporations or individuals. RENO is retina prepared, translation ready, parallax ready and much more. It contains 6 Superior Sliders (Layer Slider, Revolution Slider, Nivo Slider, Sly Slider, Refine Slider and Flex Slider). It's an effective way to current your work at the highest level. It is based on widespread Twitter Bootstrap three framework. This theme makes use of Visible Composer and the newest HTML5 and CSS3 technologies. Save additional $70 for premium content included in Reno theme. Add or extract the woocommerce-mailchimp folder to your web site’s /wp-content material/plugins/ directory. You can too use the Add new possibility discovered in the Plugins menu in WordPress.
With both WooCommerce and Cart66, your prospects shop completely on your WordPress site With WooCommerce your product pages are normally customized post sorts where you enter your product descriptions, add product photos, and so on. In Cart66 individuals usually organize their merchandise as normal WordPress posts and use the inbuilt features that WordPress provides to organize the products in the identical method that you'd set up weblog posts into classes. The general level is that with each WooCommerce and Cart66 all of your product pages are in WordPress and your customers are shopping on your WordPress web site. Differences between WooCommerce and Cart66.
Digitalis is a multipurpose WordPress theme with a clear and colorful design and plenty of distinction. With blog, journal, and WooCommerce functionality, Digitalis has the options to help construct a successful site in any niche. It includes custom icons, shortcodes and far more. Tyrion is a parallax eCommerce theme optimized for WooCommerce WordPress plugin. The theme is totally responsive and optimized for all machine display sizes. Should you loved this post and you would like to receive more info about http://bestwoocommercethemes.blogspot.co.uk/2014/05/the-ultimate-top-5-responsive-themes.html kindly visit the page. You'll be able to simply customize the small elements of the theme akin to updating brand, changing colors, fonts, background picture by way of internet interface. Set your rule’s values and choose the classes you want to apply your rule to. Creating Site Extensive Rules
First, modifications to the way the frontend of your store could also be related to your theme (i.e., the best way product pages show), as some third-occasion themes haven't been updated to be suitable. See this debugging information to determine if a theme situation exists, and if that's the case, contact your theme supplier to ask them to replace for WooCommerce 2.1. In case you have 404 errors in every single place, this can be mounted, and might be in WooCommerce 2.1.1. In the meantime, you can manually flush permalinks by re-saving the Settings > Permalinks page in your WordPress admin.
Bitruncated tesseract
| Bitruncated tesseract | ||
|---|---|---|
  Two Schlegel diagrams, centered on truncated tetrahedral or truncated octahedral cells, with alternate cell types hidden. | ||
| Type | Uniform polychoron | |
| Schläfli symbol | 2t{4,3,3} 2t{3,31,1} h2,3{4,3,3} | |
| Coxeter-Dynkin diagrams | Template:CDD Template:CDD Template:CDD = Template:CDD | |
| Cells | 24 | 8 4.6.6 16 3.6.6 |
| Faces | 120 | 32 {3} 24 {4} 64 {6} |
| Edges | 192 | |
| Vertices | 96 | |
| Vertex figure | 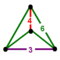 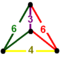 Digonal disphenoid | |
| Symmetry group | BC4, [3,3,4], order 384 D4, [31,1,1], order 192 | |
| Properties | convex, vertex-transitive | |
| Uniform index | 15 16 17 | |
The bitruncated tesseract or bitruncated 16-cell is constructed by a bitruncation operation applied to the tesseract. It can also be called a runcicantic tesseract with half the vertices of a runcicantellated tesseract with a Template:CDD construction.
Alternate names
- Bitruncated tesseract/Runcicantic tesseract (Norman W. Johnson)
- Bitruncated tesseract (Acronym tah) (George Olshevsky, and Jonathan Bowers)[2]
Construction
A tesseract is bitruncated by truncating its cells beyond their mid-points, turning the eight cubes into eight truncated octahedra. These still share their square faces, but the hexagonal faces form truncated tetrahedra which share their triangular faces with each other.
The Cartesian coordinates of the vertices of a bitruncated tesseract having edge length 2 is given by all permutations of:
Structure
The truncated octahedra are connected to each other via their square faces, and to the truncated tetrahedra via their hexagonal faces. The truncated tetrahedra are connected to each other via their triangular faces.
Projections
Template:4-cube Coxeter plane graphs
Stereographic projections
The truncated-octahedron-first projection of the bitruncated tesseract into 3D space has a truncated cubical envelope. Two of the truncated octahedral cells project onto a truncated octahedron inscribed in this envelope, with the square faces touching the centers of the octahedral faces. The 6 octahedral faces are the images of the remaining 6 truncated octahedral cells. The remaining gap between the inscribed truncated octahedron and the envelope are filled by 8 flattened truncated tetrahedra, each of which is the image of a pair of truncated tetrahedral cells.

|
 Colored transparently with pink triangles, blue squares, and gray hexagons |
Related polytopes
The bitruncated tesseract is second in a sequence of bitruncated hypercubes:
My name is Margene (46 years old) and my hobbies are Baton twirling and Photography.
my web blog: hombre embarazado (http://Www.Tumaternidad.com)
Truncated 16-cell
| Truncated 16-cell Cantic tesseract | ||
|---|---|---|
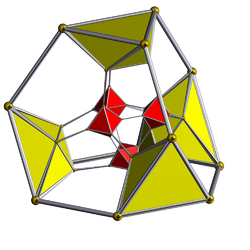 Schlegel diagram (octahedron cells visible) | ||
| Type | Uniform polychoron | |
| Schläfli symbol | t{4,3,3} t{3,31,1} h2{4,3,3} | |
| Coxeter-Dynkin diagrams | Template:CDD Template:CDD Template:CDD = Template:CDD | |
| Cells | 24 | 8 3.3.3.3 16 3.6.6 |
| Faces | 96 | 64 {3} 32 {6} |
| Edges | 120 | |
| Vertices | 48 | |
| Vertex figure |  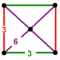 square pyramid | |
| Dual | Hexakis tesseract | |
| Coxeter groups | BC4 [3,3,4], order 384 D4 [31,1,1], order 192 | |
| Properties | convex | |
| Uniform index | 16 17 18 | |
The truncated 16-cell or cantic tesseract which is bounded by 24 cells: 8 regular octahedra, and 16 truncated tetrahedra. It has half the vertices of a cantellated tesseract with construction Template:CDD.
It is related to, but not to be confused with, the 24-cell, which is a regular polychoron bounded by 24 regular octahedra.
Alternate names
- Truncated 16-cell/Cantic tesseract (Norman W. Johnson)
- Truncated hexadecachoron (Acronym thex) (George Olshevsky, and Jonathan Bowers)[3]
Construction
The truncated 16-cell may be constructed from the 16-cell by truncating its vertices at 1/3 of the edge length. This results in the 16 truncated tetrahedral cells, and introduces the 8 octahedra (vertex figures).
(Truncating a 16-cell at 1/2 of the edge length results in the 24-cell, which has a greater degree of symmetry because the truncated cells become identical with the vertex figures.)
The Cartesian coordinates of the vertices of a truncated 16-cell having edge length 2√2 are given by all permutations, and sign combinations:
- (0,0,1,2)
An alternate construction begins with a demitesseract with vertex coordinates (±3,±3,±3,±3), having an even number of each sign, and truncates it to obtain the permutations of
- (1,1,3,3), with an even number of each sign.
Structure
The truncated tetrahedra are joined to each other via their hexagonal faces. The octahedra are joined to the truncated tetrahedra via their triangular faces.
Projections
Centered on octahedron

The octahedron-first parallel projection of the truncated 16-cell into 3-dimensional space has the following structure:
- The projection envelope is a truncated octahedron.
- The 6 square faces of the envelope are the images of 6 of the octahedral cells.
- An octahedron lies at the center of the envelope, joined to the center of the 6 square faces by 6 edges. This is the image of the other 2 octahedral cells.
- The remaining space between the envelope and the central octahedron is filled by 8 truncated tetrahedra (distorted by projection). These are the images of the 16 truncated tetrahedral cells, a pair of cells to each image.
This layout of cells in projection is analogous to the layout of faces in the projection of the truncated octahedron into 2-dimensional space. Hence, the truncated 16-cell may be thought of as the 4-dimensional analogue of the truncated octahedron.
50 year old Petroleum Engineer Kull from Dawson Creek, spends time with interests such as house brewing, property developers in singapore condo launch and camping. Discovers the beauty in planing a trip to places around the entire world, recently only coming back from .
Centered on truncated tetrahedron

The truncated tetrahedron first parallel projection of the truncated 16-cell into 3-dimensional space has the following structure:
- The projection envelope is a truncated cube.
- The nearest truncated tetrahedron to the 4D viewpoint projects to the center of the envelope, with its triangular faces joined to 4 octahedral volumes that connect it to 4 of the triangular faces of the envelope.
- The remaining space in the envelope is filled by 4 other truncated tetrahedra.
- These volumes are the images of the cells lying on the near side of the truncated 16-cell; the other cells project onto the same layout except in the dual configuration.
- The six octagonal faces of the projection envelope are the images of the remaining 6 truncated tetrahedral cells.
50 year old Petroleum Engineer Kull from Dawson Creek, spends time with interests such as house brewing, property developers in singapore condo launch and camping. Discovers the beauty in planing a trip to places around the entire world, recently only coming back from .
Images
Template:4-cube Coxeter plane graphs
 Net |
 Stereographic projection (centered on truncated tetrahedron) |
Related uniform polytopes
Notes
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Template:PolyCell
- Template:KlitzingPolytopes o3o3o4o - tat, o3x3x4o - tah, x3x3o4o - thex
External links
- Paper model of truncated tesseract created using nets generated by Stella4D software