Ornstein isomorphism theorem

In probability and statistics a Markov renewal process is a random process that generalizes the notion of Markov jump processes. Other random processes like Markov chain, Poisson process, and renewal process can be derived as a special case of an MRP (Markov renewal process).

Definition

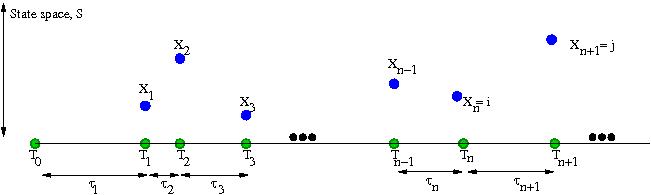
Consider a state space $\mathrm{S}.$ Consider a set of random variables $(X_n,T_n)$, where $T_n$ are the jump times and $X_n$ are the associated states in the Markov chain (see Figure). Let the inter-arrival time, ${\tau }_n=T_n-T_{n-1}$. Then the sequence (X_n, T_n) is called a Markov renewal process if

$\mathrm{Pr}({\tau }_{n+1}\le t,X_{n+1}=j|(X_0,T_0),(X_1,T_1),\dots ,(X_n=i,T_n))$

$=\mathrm{Pr}({\tau }_{n+1}\le t,X_{n+1}=j|X_n=i)\mathrm{\forall }n\ge 1,t\ge 0,i,j\in \mathrm{S}$

An illustration of a Markov renewal process

Relation to other stochastic processes

1. If we define a new stochastic process $Y_t:=X_n$ for $t\in [T_n,T_{n+1})$, then the process $Y_t$ is called a semi-Markov process. Note the main difference between an MRP and a semi-Markov process is that the former is defined as a two-tuple of states and times, whereas the latter is the actual random process that evolves over time. The entire process is not Markovian, i.e., memoryless, as happens in a CTMC. Instead the process is Markovian only at the specified jump instants. This is the rationale behind the name, Semi-Markov.
2. A semi-Markov process where all the holding times are exponentially distributed is called a continuous time Markov chain/process (CTMC). In other words, if the inter-arrival times are exponentially distributed and if the waiting time in a state and the next state reached are independent, we have a CTMC.

   $\mathrm{Pr}({\tau }_{n+1}\le t,X_{n+1}=j|(X_0,T_0),(X_1,T_1),\dots ,(X_n=i,T_n))=\mathrm{Pr}({\tau }_{n+1}\le t,X_{n+1}=j|X_n=i)$

   $=\mathrm{Pr}(X_{n+1}=j|X_n=i)(1-e^{-{\lambda }_{i}t}),\text{ for all }n\ge 1,t\ge 0,i,j\in \mathrm{S}$

3. The sequence $X_n$ in the MRP is a discrete-time Markov chain. In other words, if the time variables are ignored in the MRP equation, we end up with a DTMC.

   $\mathrm{Pr}(X_{n+1}=j|X_0,X_1,\dots ,X_n=i)=\mathrm{Pr}(X_{n+1}=j|X_n=i)\mathrm{\forall }n\ge 1,i,j\in \mathrm{S}$

4. If the sequence of $\tau$s are independent and identically distributed, and if their distribution does not depend on the state $X_n$, then the process is a renewal process. So, if the exact states are ignored and we have a chain of iid times, then we have a renewal process.

   $\mathrm{Pr}({\tau }_{n+1}\le t|T_0,T_1,\dots ,T_n)=\mathrm{Pr}({\tau }_{n+1}\le t)\mathrm{\forall }n\ge 1,\mathrm{\forall }t\ge 0$

See also

• Markov process
• Renewal theory
• Variable-order Markov model

References and Further Reading

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.