Infinity: Difference between revisions
en>Hydrox →Computing: the Infinity values behave (in relation to other numeric values) correctly as primitives (see given chapters in the spec) E.g. x is any number except NaN follows expression (x <= Infinite) is true (and same for -Infinite and >=) |
en>INeverCry m Reverted edits by 173.162.164.121 (talk) to last version by ClueBot NG |
||
| Line 1: | Line 1: | ||
[[File:Optical phase space.jpg|thumb|400px|right|Optical phase diagram of a coherent state's distribution across phase space.]] | |||
In [[quantum optics]], an '''optical phase space''' is a [[phase space]] in which all [[quantum state]]s of an [[optical system]] are described. Each point in the optical phase space corresponds to a unique state of an ''optical system''. For any such system, a plot of the ''quadratures'' against each other, possibly as functions of time, is called a [[phase diagram]]. If the quadratures are functions of time then the optical phase diagram can show the evolution of a quantum optical system with time. | |||
An optical phase diagram can give insight into the properties and behaviors of the system that might otherwise not be obvious. This can allude to qualities of the system that can be of interest to an individual studying an optical system that would be very hard to deduce otherwise. Another use for an optical phase diagram is that it shows the evolution of the state of an optical system. This can be used to determine the state of the optical system at any point in time. | |||
==Background information== | |||
When discussing the quantum theory of light, it is very common to use an electromagnetic [[oscillator]] as a model.<ref name="Measuring the Quantum State of Light">{{cite book|first=Ulf |last=Leonhardt |title=Measuring the Quantum State of Light |pages=18–29| publisher=[[Cambridge University Press]] |location=Cambridge |year=2005 |isbn=0-521-02352-1}}</ref> An electromagnetic oscillator describes an oscillation of the electric field. Since the magnetic field is proportional to the rate of change of the electric field, this too oscillates. Such oscillations describe light. Systems composed of such oscillators can be described by an optical phase space. | |||
Let '''u'''('''x''',t) be a [[vector function]] describing a [[single mode]] of an [[simple harmonic oscillator|electromagnetic oscillator]]. For simplicitity, it is assumed that this electromagnetic oscillator is in vacuum. An example is the [[plane wave]] given by | |||
:<math> \mathbf{u}(\mathbf{x},t) = \mathbf{u_{0}}e^{i(\mathbf{k} \cdot \mathbf{x} - wt)} </math> | |||
where '''u<sub>0</sub>''' is the [[polarization vector]], '''k''' is the [[wave vector]], '''w''' the frequency, and '''A'''<math>\cdot </math>'''B''' denotes the [[dot product]] between the [[Euclidean vector|vectors]] '''A''' and '''B'''. This is the equation for a [[plane wave]] and is a simple example of such an electromagnetic oscillator. The oscillators being examined could either be free waves in space or some normal mode contained in some [[cavity]]. | |||
A single mode of the electromagnetic oscillator is isolated from the rest of the system and examined. Such an oscillator, when quantized, is described by the mathematics of a [[quantum harmonic oscillator]].<ref name="Measuring the Quantum State of Light"/> Quantum oscillators are described using [[creation and annihilation operators]] <math>\widehat a^\dagger</math> and <math>\widehat a</math>. Physical quantities, such as the [[electric field strength]], then become [[operator (physics)|quantum operators]]. | |||
In order to distinguish a physical quantity from the quantum mechanical operator used to describe it, a "hat" is used over the operator symbols. Thus, for example, where <math>E_i</math> might represent (one component of) the [[electric field]], the symbol <math>\widehat E_i</math> denotes the quantum-mechanical operator that describes <math>E_i</math>. This convention is used throughout this article, but is not in common use in more advanced texts, which avoid the hat, as it simply clutters the text. | |||
In the quantum oscillator mode, most operators representing physical quantities are typically expressed in terms of the creation and annihilation operators. In this example, the electric field strength is given by: | |||
:<math>\widehat{E}_{i}=u_{i}^{*}(\mathbf{x},t)\widehat{a}^{\dagger} + u_{i}(\mathbf{x},t)\widehat{a}</math><ref name="Quantum Optics">{{cite book |author=Scully, Marlan; Zubairy, M. Suhail |title=Quantum Optics |pages=5| publisher=[[Cambridge University Press]] |location=Cambridge |year=1997 |isbn=0-521-43595-1}}</ref> | |||
(where ''x<sub>i</sub>'' is a single component of '''x''', position). The [[Hamiltonian (quantum mechanics)|Hamiltonian]] for an electromagnetic oscillator is found by [[Quantization (physics)|quantizing]] the [[electromagnetic field]] for this oscillator and the formula is given by: | |||
:<math>\widehat{H} = \hbar\omega (\widehat{a}^{\dagger}\widehat{a} + 1/2)</math><ref name="Quantum Optics"/> | |||
where <math>\omega</math> is the frequency of the (spatio-temportal) mode. The annihilation operator is the bosonic annihilation operator and so it obeys the [[canonical commutation relation]] given by: | |||
:<math>[\widehat{a},\widehat{a}^{\dagger}] = 1</math> | |||
The eigenstates of the annihilation operator are called [[coherent states]]: | |||
:<math>\widehat{a}|\alpha\rangle = \alpha|\alpha\rangle</math> | |||
It is important to note that the annihilation operator is not [[Hermitian]]; therefore its eigenvalues <math>\alpha</math> can be complex. This has important consequences. | |||
Finally, the [[photon number]] is given by the operator <math> \widehat{N} = \widehat{a}^{\dagger} \widehat{a},</math> which gives the number of photons in the given (spatial-temporal) mode '''u'''. | |||
==Quadratures== | |||
[[Operator (mathematics)|Operators]] given by | |||
:<math> \widehat q = \tfrac 1 {\sqrt 2}(\widehat a^\dagger + \widehat a)</math> | |||
and | |||
:<math> \widehat p = \tfrac i {\sqrt 2}(\widehat a^\dagger - \widehat a)</math> | |||
are called the quadratures and they represent the [[real number|real]] and [[imaginary number|imaginary]] parts of the complex amplitude represented by <math> \widehat a</math>.<ref name="Measuring the Quantum State of Light"/> The commutation relation between the two quadratures can easily be calculated: | |||
:<math> | |||
\begin{align} | |||
\left[ \widehat q, \widehat p \right] | |||
&= \tfrac i 2 [\widehat a^\dagger + \widehat a, \widehat a^\dagger - \widehat a] \\ | |||
&= \tfrac i 2 ([\widehat a^\dagger, \widehat a^\dagger] - [\widehat a^\dagger, \widehat a] + | |||
[\widehat a, \widehat a^\dagger] - [\widehat a, \widehat a]) \\ | |||
&= \tfrac i 2 (-(-1) + 1) \\ | |||
&= i | |||
\end{align} | |||
</math> | |||
This looks very similar to the commutation relation of the position and momentum operator. Thus, it can be useful to think of and treat the quadratures as the position and momentum of the oscillator although in fact they are the "in-phase and out-of-phase components of the electric field amplitude of the spatial-temporal mode", or '''u''', and have nothing really to do with the position or momentum of the electromagnetic oscillator (as it is hard to define what is meant by position and momentum for an electromagnetic oscillator).<ref name="Measuring the Quantum State of Light"/> | |||
===Properties of quadratures=== | |||
The [[eigenstates]] of the quadrature operators <math>\widehat{q}</math> and <math>\widehat{p}</math> are called the quadrature states. They satisfy the relations: | |||
:*<math> \widehat{q}|q\rangle = q |q\rangle</math> and <math>\widehat{p}|p\rangle = p |p\rangle</math> | |||
:*<math> \langle q | q'\rangle = \delta(q-q')</math> and <math>\langle p | p'\rangle = \delta(p-p')</math> | |||
:*<math> \int_{-\infty}^{\infty} |q\rangle \langle q| dq = 1 </math> and <math>\int_{-\infty}^{\infty} |p\rangle \langle p| dp = 1 </math> | |||
as these form [[Orthonormal basis|complete basis]] sets. | |||
===Important result=== | |||
The following is an important relation that can be derived from the above which justifies our interpretation that the quadratures are the real and imaginary parts of a complex <math>\alpha</math> (i.e. the in-phase and out-of-phase components of the electromagnetic oscillator) | |||
:<math> \langle\alpha|\widehat{q}|\alpha\rangle = 2^{-1/2}(\langle\alpha|\widehat{a}^{\dagger}|\alpha\rangle + \langle\alpha|\widehat{a}|\alpha\rangle) = 2^{-1/2}(\alpha^{*}\langle\alpha|\alpha\rangle + \alpha\langle\alpha|\alpha\rangle) </math> | |||
The following is a relationship that can be used to help evaluate the above and is given by: | |||
:<math>\langle\alpha'|\alpha\rangle = e^{(-1/2)(|\alpha'|^{2}+|\alpha|^{2}) + \alpha'^{*}\alpha}</math><ref name="Measuring the Quantum State of Light"/> | |||
This gives us that: | |||
:<math> \langle\alpha|\widehat{q}|\alpha\rangle = 2^{-1/2}(\alpha^{*} + \alpha) = q_{\alpha}</math> | |||
:<math> \langle\alpha|\widehat{p}|\alpha\rangle = i2^{-1/2}(\alpha^{*} - \alpha) = p_{\alpha} </math> by a similar method as above. | |||
:<math> \alpha = 2^{-1/2}(\langle\alpha|\widehat{q}|\alpha\rangle + i\langle\alpha|\widehat{p}|\alpha\rangle) = 2^{-1/2}(q_{\alpha} + ip_{\alpha}) </math> | |||
Thus, <math>\alpha</math> is just a composition of the quadratures. | |||
Another very important property of the coherent states becomes very apparent in this formalism. A coherent state is not a point in the optical phase space but rather a distribution on it. This can be seen via | |||
:<math>q_{\alpha} = \langle\alpha|\widehat{q}|\alpha\rangle</math> | |||
and | |||
:<math>p_{\alpha} = \langle\alpha|\widehat{p}|\alpha\rangle</math>. | |||
These are only the expectation values of <math>\widehat{q}</math> and <math>\widehat{p}</math> for the state <math>|\alpha\rangle</math>. | |||
It can be shown that the quadratures obey [[Heisenberg's Uncertainty Principle]] given by: | |||
:<math>\Delta q\Delta p \ge 1/2</math><ref name="Measuring the Quantum State of Light"/> (where <math>\Delta q</math> and <math>\Delta p</math> are the [[variance]]s of the distributions of q and p, respectively) | |||
This inequality does not necessarily have to be saturated and a common example of such states are [[squeezed coherent states]]. The coherent states are [[Gaussian probability distribution]]s over the phase space localized around <math>\alpha</math>. | |||
==Operators on phase space== | |||
It is possible to define operators to move the coherent states around the phase space. These can produce new coherent states and allow us to move around phase space. | |||
===Phase-shifting operator=== | |||
[[File:Rotation operator.jpg|thumb|350px|right|Phase shifting operator acting on a coherent state rotating it by an angle <math>\theta</math> in phase space.]] | |||
The phase-shifting operator rotates the coherent state by an angle <math>\theta</math> in the optical phase space. This operator is given by: | |||
:<math> \widehat{U}(\theta) = e^{-i\theta\widehat{N}} </math> <ref name="Measuring the Quantum State of Light"/> | |||
The important relationship | |||
:<math> \widehat{U}(\theta)^{\dagger}\widehat{a}\widehat{U}(\theta) = \widehat{a}e^{-i\theta} </math> | |||
is derived as follows: | |||
:<math> d/d\theta (\widehat{U}^{\dagger}\widehat{a}\widehat{U}) = i\widehat{n}\widehat{U}^{\dagger}\widehat{a}\widehat{U} - i\widehat{U}^{\dagger}\widehat{a}\widehat{U}\widehat{N} = \widehat{U}^{\dagger}i[\widehat{N},\widehat{a}]\widehat{U}</math> | |||
:<math>= \widehat{U}^{\dagger}i(\widehat{a}^{\dagger}\widehat{a}\widehat{a} - \widehat{a}\widehat{a}^{\dagger}\widehat{a})\widehat{U} = \widehat{U}^{\dagger}i[\widehat{a}^{\dagger},\widehat{a}]\widehat{a}\widehat{U} = -i\widehat{U}^{\dagger}\widehat{a}\widehat{U}</math> | |||
and solving this [[differential equation]] yields the desired result. | |||
Thus, using the above it becomes clear that | |||
:<math>\widehat{U}(\theta)|\alpha\rangle = |\alpha e^{-i\theta}\rangle</math>, | |||
or a rotation by an angle theta on the coherent state in phase space. The following illustrates this more clearly: | |||
:<math>\widehat{a}(\widehat{U}|\alpha\rangle) = \widehat{U}\widehat{a}e^{-i\theta}|\alpha\rangle </math> | |||
(which is obtained using the fact that the phase-shifting operator is [[unitary]]{{Disambiguation needed|date=January 2012}}) | |||
:<math> \widehat{a}(\widehat{U}|\alpha\rangle) = \widehat{U} \alpha e^{-i\theta}|\alpha\rangle = \alpha e^{-i\theta}(\widehat{U}|\alpha\rangle) </math> | |||
Thus, | |||
:<math>(\alpha e^{-i\theta}, \widehat{U}|\alpha\rangle) </math> | |||
is the [[Eigenvalue, eigenvector and eigenspace|eigenpair]] of | |||
:<math> \widehat{a}\widehat{U}|\alpha\rangle</math>. | |||
From this it is possible to see that | |||
:<math> (\alpha e^{-i\theta} = 2^{-1/2}[q_{\alpha} cos(\theta) + p_{\alpha} sin(\theta)] + i2^{-1/2}[-q_{\alpha} csin(\theta) + p_{\alpha} cos(\theta)], \widehat{U}|\alpha\rangle = |\alpha e^{-i\theta}\rangle)</math> | |||
which is another way of expressing the eigenpair which more clearly illustrates the effects of the phase-shifting operator on coherent states. | |||
===Displacement operator=== | |||
[[File:Displacement operator.jpg|thumb|350px|right|Displacement operator acting on a coherent state displacing it by some value <math>\alpha</math> in phase space.]] | |||
The displacement operator takes a coherent state and moves it (by some value) to another coherent state somewhere in the phase space. The displacement operator is given by: | |||
:<math>\widehat{D}(\alpha) = e^{\alpha\widehat{a}^{\dagger} - \alpha^{*}\widehat{a}}</math> | |||
The relationship | |||
:<math> \widehat{D}^{\dagger}\widehat{a}\widehat{D} = \widehat{a} + \alpha</math>.<ref name="Measuring the Quantum State of Light"/> | |||
can be derived quite easily. | |||
To do this, take an infinitesimal displacement <math>\delta\alpha</math>. | |||
The operators <math>\widehat{D}</math> and <math>\widehat{D}^{\dagger}</math> can be expanded in terms of the identity | |||
:<math>e^{x} = \sum_{0}^{\infty}x^{i}/i!</math> | |||
and look at the first order terms and ignore all the higher order terms (all higher order terms are very close to zero as <math>\delta\alpha</math> is very small). | |||
Thus: | |||
:<math> \widehat{D}^{\dagger}(\delta\alpha)\widehat{a}\widehat{D}(\delta\alpha) = \sum_{i,j}(\delta\alpha^{*}\widehat{a} - \delta\alpha\widehat{a}^{\dagger})^{i}\widehat{a}(\delta\alpha\widehat{a}^{\dagger}-\delta\alpha^{*}\widehat{a})^{j}/i!j!</math> | |||
:<math>=\widehat{a} + (\delta\alpha^{*}\widehat{a} - \delta\alpha\widehat{a}^{\dagger})\widehat{a} + \widehat{a}(\delta\alpha\widehat{a}^{\dagger} - \delta\alpha^{*}\widehat{a}) + O(\delta\alpha^{2},(\delta\alpha^{*})^{2})</math> (but as given above, the higher order terms are very close to zero and therefore neglected) | |||
:<math>=\widehat{a} + \widehat{a}(\delta\alpha\widehat{a}^{\dagger} - \delta\alpha^{*}\widehat{a}) - (\delta\alpha\widehat{a}^{\dagger} - \delta\alpha^{*}\widehat{a})\widehat{a}</math> | |||
:<math>=\widehat{a} + [\widehat{a},\delta\alpha\widehat{a}^{\dagger} - \delta\alpha^{*}\widehat{a}] = \widehat{a} + \delta\alpha[\widehat{a},\widehat{a}^{\dagger}] - \delta\alpha^{*}[\widehat{a},\widehat{a}]</math> (use the identity from above) | |||
:<math> \widehat{D}^{\dagger}(\delta\alpha)\widehat{a}\widehat{D}(\delta\alpha)=\widehat{a} + \delta\alpha</math> | |||
The above identity can be applied repeatedly in the following fashion to derive the following: | |||
:<math> (\widehat{D}^{\dagger}(\delta\alpha))^{k}\widehat{a}(\widehat{D}(\delta\alpha))^{k} = \widehat{a} + k\delta\alpha</math> | |||
Thus, the above identity suggests that repeated use of the displacement operator generates translations in phase space. | |||
====Important consequence==== | |||
The following is an important consequence of the displacement vector. | |||
First note that the displacement operator is a [[unitary operator]]. Use | |||
:<math> \widehat{D}^{\dagger}(\delta\alpha)\widehat{a}\widehat{D}(\delta\alpha)=\widehat{a} + \delta\alpha</math> | |||
to get: | |||
:<math>\widehat{a}\widehat{D}(-\alpha)|\alpha\rangle = \widehat{D}(-\alpha)(\widehat{a} - \alpha)|\alpha\rangle</math> | |||
:<math>=\widehat{D}(-\alpha)(\widehat{a}|\alpha\rangle - \alpha|\alpha\rangle)</math> | |||
:<math>=\widehat{D}(-\alpha)(\alpha|\alpha\rangle - \alpha|\alpha\rangle)</math> | |||
Thus, | |||
:<math>\widehat{a}(\widehat{D}(-\alpha)|\alpha\rangle)=0</math> | |||
or it follows that | |||
:<math>\widehat{D}(-\alpha)|\alpha\rangle = |0\rangle</math> | |||
which leads to | |||
:<math>|\alpha\rangle=\widehat{D}(\alpha)|0\rangle</math>. | |||
This is important as it suggests that all coherent states are just displacements of the [[ground state]], which in optics is also the [[vacuum state]]. That is, any coherent state can be generated via the displacement of the ground state of the electromagnetic oscillator from above. | |||
==See also== | |||
* [[Nonclassical light]] | |||
* [[Rotation operator (quantum mechanics)]] | |||
* [[Quantum harmonic oscillator]] | |||
* [[Quasiprobability distribution]] | |||
* [[Husimi Q representation]] | |||
* [[Squeezed coherent state]] | |||
* [[Wigner function]] | |||
==References== | |||
{{reflist}} | |||
[[Category:Quantum optics| ]] | |||
[[Category:Optics]] | |||
Revision as of 21:29, 28 January 2014
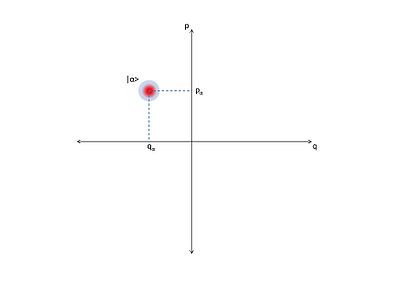
In quantum optics, an optical phase space is a phase space in which all quantum states of an optical system are described. Each point in the optical phase space corresponds to a unique state of an optical system. For any such system, a plot of the quadratures against each other, possibly as functions of time, is called a phase diagram. If the quadratures are functions of time then the optical phase diagram can show the evolution of a quantum optical system with time.
An optical phase diagram can give insight into the properties and behaviors of the system that might otherwise not be obvious. This can allude to qualities of the system that can be of interest to an individual studying an optical system that would be very hard to deduce otherwise. Another use for an optical phase diagram is that it shows the evolution of the state of an optical system. This can be used to determine the state of the optical system at any point in time.
Background information
When discussing the quantum theory of light, it is very common to use an electromagnetic oscillator as a model.[1] An electromagnetic oscillator describes an oscillation of the electric field. Since the magnetic field is proportional to the rate of change of the electric field, this too oscillates. Such oscillations describe light. Systems composed of such oscillators can be described by an optical phase space.
Let u(x,t) be a vector function describing a single mode of an electromagnetic oscillator. For simplicitity, it is assumed that this electromagnetic oscillator is in vacuum. An example is the plane wave given by
where u0 is the polarization vector, k is the wave vector, w the frequency, and AB denotes the dot product between the vectors A and B. This is the equation for a plane wave and is a simple example of such an electromagnetic oscillator. The oscillators being examined could either be free waves in space or some normal mode contained in some cavity.
A single mode of the electromagnetic oscillator is isolated from the rest of the system and examined. Such an oscillator, when quantized, is described by the mathematics of a quantum harmonic oscillator.[1] Quantum oscillators are described using creation and annihilation operators and . Physical quantities, such as the electric field strength, then become quantum operators.
In order to distinguish a physical quantity from the quantum mechanical operator used to describe it, a "hat" is used over the operator symbols. Thus, for example, where might represent (one component of) the electric field, the symbol denotes the quantum-mechanical operator that describes . This convention is used throughout this article, but is not in common use in more advanced texts, which avoid the hat, as it simply clutters the text.
In the quantum oscillator mode, most operators representing physical quantities are typically expressed in terms of the creation and annihilation operators. In this example, the electric field strength is given by:
(where xi is a single component of x, position). The Hamiltonian for an electromagnetic oscillator is found by quantizing the electromagnetic field for this oscillator and the formula is given by:
where is the frequency of the (spatio-temportal) mode. The annihilation operator is the bosonic annihilation operator and so it obeys the canonical commutation relation given by:
The eigenstates of the annihilation operator are called coherent states:
It is important to note that the annihilation operator is not Hermitian; therefore its eigenvalues can be complex. This has important consequences.
Finally, the photon number is given by the operator which gives the number of photons in the given (spatial-temporal) mode u.
Quadratures
Operators given by
and
are called the quadratures and they represent the real and imaginary parts of the complex amplitude represented by .[1] The commutation relation between the two quadratures can easily be calculated:
This looks very similar to the commutation relation of the position and momentum operator. Thus, it can be useful to think of and treat the quadratures as the position and momentum of the oscillator although in fact they are the "in-phase and out-of-phase components of the electric field amplitude of the spatial-temporal mode", or u, and have nothing really to do with the position or momentum of the electromagnetic oscillator (as it is hard to define what is meant by position and momentum for an electromagnetic oscillator).[1]
Properties of quadratures
The eigenstates of the quadrature operators and are called the quadrature states. They satisfy the relations:
as these form complete basis sets.
Important result
The following is an important relation that can be derived from the above which justifies our interpretation that the quadratures are the real and imaginary parts of a complex (i.e. the in-phase and out-of-phase components of the electromagnetic oscillator)
The following is a relationship that can be used to help evaluate the above and is given by:
This gives us that:
Thus, is just a composition of the quadratures.
Another very important property of the coherent states becomes very apparent in this formalism. A coherent state is not a point in the optical phase space but rather a distribution on it. This can be seen via
and
These are only the expectation values of and for the state .
It can be shown that the quadratures obey Heisenberg's Uncertainty Principle given by:
This inequality does not necessarily have to be saturated and a common example of such states are squeezed coherent states. The coherent states are Gaussian probability distributions over the phase space localized around .
Operators on phase space
It is possible to define operators to move the coherent states around the phase space. These can produce new coherent states and allow us to move around phase space.
Phase-shifting operator
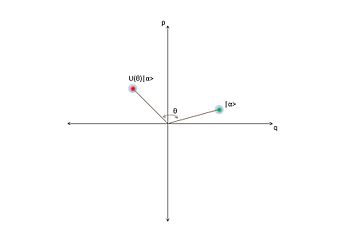
The phase-shifting operator rotates the coherent state by an angle in the optical phase space. This operator is given by:
The important relationship
is derived as follows:
and solving this differential equation yields the desired result.
Thus, using the above it becomes clear that
or a rotation by an angle theta on the coherent state in phase space. The following illustrates this more clearly:
(which is obtained using the fact that the phase-shifting operator is unitaryTemplate:Disambiguation needed)
Thus,
is the eigenpair of
From this it is possible to see that
which is another way of expressing the eigenpair which more clearly illustrates the effects of the phase-shifting operator on coherent states.
Displacement operator

The displacement operator takes a coherent state and moves it (by some value) to another coherent state somewhere in the phase space. The displacement operator is given by:
The relationship
- .[1]
can be derived quite easily.
To do this, take an infinitesimal displacement .
The operators and can be expanded in terms of the identity
and look at the first order terms and ignore all the higher order terms (all higher order terms are very close to zero as is very small).
Thus:
The above identity can be applied repeatedly in the following fashion to derive the following:
Thus, the above identity suggests that repeated use of the displacement operator generates translations in phase space.
Important consequence
The following is an important consequence of the displacement vector.
First note that the displacement operator is a unitary operator. Use
to get:
Thus,
or it follows that
which leads to
This is important as it suggests that all coherent states are just displacements of the ground state, which in optics is also the vacuum state. That is, any coherent state can be generated via the displacement of the ground state of the electromagnetic oscillator from above.
See also
- Nonclassical light
- Rotation operator (quantum mechanics)
- Quantum harmonic oscillator
- Quasiprobability distribution
- Husimi Q representation
- Squeezed coherent state
- Wigner function
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 2.0 2.1 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534









![{\displaystyle [{\widehat {a}},{\widehat {a}}^{\dagger }]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6fe4cd3c1a473006a6cfe0cbe5dc6221781dfeb)





![{\displaystyle {\begin{aligned}\left[{\widehat {q}},{\widehat {p}}\right]&={\tfrac {i}{2}}[{\widehat {a}}^{\dagger }+{\widehat {a}},{\widehat {a}}^{\dagger }-{\widehat {a}}]\\&={\tfrac {i}{2}}([{\widehat {a}}^{\dagger },{\widehat {a}}^{\dagger }]-[{\widehat {a}}^{\dagger },{\widehat {a}}]+[{\widehat {a}},{\widehat {a}}^{\dagger }]-[{\widehat {a}},{\widehat {a}}])\\&={\tfrac {i}{2}}(-(-1)+1)\\&=i\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a46ea7c8ca86e109ea8a5f65884b4d8560080c3)






















![d/d\theta ({\widehat {U}}^{{\dagger }}{\widehat {a}}{\widehat {U}})=i{\widehat {n}}{\widehat {U}}^{{\dagger }}{\widehat {a}}{\widehat {U}}-i{\widehat {U}}^{{\dagger }}{\widehat {a}}{\widehat {U}}{\widehat {N}}={\widehat {U}}^{{\dagger }}i[{\widehat {N}},{\widehat {a}}]{\widehat {U}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6b1c46ce4a3ab6110368954e207ce3c649449d5)
![{\displaystyle ={\widehat {U}}^{\dagger }i({\widehat {a}}^{\dagger }{\widehat {a}}{\widehat {a}}-{\widehat {a}}{\widehat {a}}^{\dagger }{\widehat {a}}){\widehat {U}}={\widehat {U}}^{\dagger }i[{\widehat {a}}^{\dagger },{\widehat {a}}]{\widehat {a}}{\widehat {U}}=-i{\widehat {U}}^{\dagger }{\widehat {a}}{\widehat {U}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e01dbefc43dbd3190b35020b954014a6e3bd5a79)





![{\displaystyle (\alpha e^{-i\theta }=2^{-1/2}[q_{\alpha }cos(\theta )+p_{\alpha }sin(\theta )]+i2^{-1/2}[-q_{\alpha }csin(\theta )+p_{\alpha }cos(\theta )],{\widehat {U}}|\alpha \rangle =|\alpha e^{-i\theta }\rangle )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/621b1ca37ecb4f0b2b57b38c2f8424438d357435)









![{\displaystyle ={\widehat {a}}+[{\widehat {a}},\delta \alpha {\widehat {a}}^{\dagger }-\delta \alpha ^{*}{\widehat {a}}]={\widehat {a}}+\delta \alpha [{\widehat {a}},{\widehat {a}}^{\dagger }]-\delta \alpha ^{*}[{\widehat {a}},{\widehat {a}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfa3b45ed56d115eaef8c29f8838d3ff2c88be66)







