Torsion-free abelian group

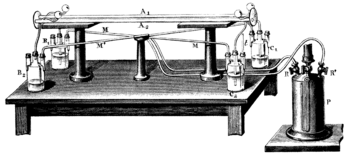
The Fizeau experiment was carried out by Hippolyte Fizeau in 1851 to measure the relative speeds of light in moving water. Fizeau used a special interferometer arrangement to measure the effect of movement of a medium upon the speed of light.^{[P 1]}^{[P 2]}

According to the theories prevailing at the time, light traveling through a moving medium would be dragged along by the medium, so that the measured speed of the light would be a simple sum of its speed through the medium plus the speed of the medium. Fizeau indeed detected a dragging effect, but the magnitude of the effect that he observed was far lower than expected. His results seemingly supported the partial aether-drag hypothesis of Fresnel, a situation that was disconcerting to most physicists. Over half a century passed before a satisfactory explanation of Fizeau's unexpected measurement was developed with the advent of Albert Einstein's theory of special relativity. Einstein later pointed out the importance of the experiment for special relativity.^{[S 1]}^{[S 2]}^{[S 3]}

Although it is referred to as the Fizeau experiment, Fizeau was an active experimenter who carried out a wide variety of different experiments involving measuring the speed of light in different situations.

Experimental setup

A light ray emanating from the source S' is reflected by a beam splitter G and is collimated into a parallel beam by lens L. After passing the slits O₁ and O₂, two rays of light travel through the tubes A₁ and A₂, through which water is streaming back and forth as shown by the arrows. The rays reflect off a mirror m at the focus of lens L', so that one ray always propagates in the same direction as the water stream, and the other ray opposite to the direction of the water stream. After passing back and forth through the tubes, both rays unite at S, where they produce interference fringes that can be visualized through the illustrated eyepiece. The interference pattern can be analyzed to determine the speed of light traveling along each leg of the tube.

Fresnel drag coefficient

Assume that water flows in the pipes at velocity v. According to the non-relativistic theory of the luminiferous aether, the speed of light should be increased when "dragged" along by the water, and decreased when "overcoming" the resistance of the water. The overall speed of a beam of light should be a simple additive sum of its speed through the water plus the speed of the water.

That is, if n is the index of refraction of water, so that c/n is the velocity of light in stationary water, then the predicted speed of light w in one arm would be

w_{+} = \frac{c}{n} + v,

and the predicted speed in the other arm would be

w_{-} = \frac{c}{n} - v,

Hence light traveling against the flow of water should be slower than light traveling with the flow of water.

The interference pattern between the two beams when the light is recombined at the observer depends upon the transit times over the two paths, and can be used to calculate the speed of light as a function of the speed of the water.^{[S 4]}

Fizeau found that

w_{+} = \frac{c}{n} + v (1 - \frac{1}{n^{2}}) .

In other words, light appeared to be dragged by the water, but the magnitude of the dragging was much lower than expected.

The Fizeau experiment forced physicists to accept the empirical validity of an old, theoretically unsatisfactory theory of Augustin-Jean Fresnel (1818) that had been invoked to explain an 1810 experiment by Arago, namely, that a medium moving through the stationary aether drags light propagating through it with only a fraction of the medium's speed, with a dragging coefficient f given by

f = (1 - \frac{1}{n^{2}}) .

In 1895, Hendrik Lorentz predicted the existence of an extra term due to dispersion:^{[S 5]}

w_{+} = \frac{c}{n} + v (1 - \frac{1}{n^{2}} - \frac{λ}{n} \cdot \frac{d n}{d λ})

.

Repetitions

Improved Fizeau type experiment by Michelson and Morley in 1886. Collimated light from source a falls on beam splitter b where it divides: one part follows the path **b c d e f b g** and the other the path **b f e d c b g**.

Albert Michelson and Edward Morley (1886)^{[P 3]} repeated Fizeau's experiment with improved accuracy, addressing several concerns with Fizeau's original experiment: (1) Deformation of the optical components in Fizeau's apparatus could cause artifactual fringe displacement; (2) observations were rushed, since the pressurized flow of water lasted only a short time; (3) Fizeau's tubes were of small diameter resulting in observational difficulties; (4) there were uncertainties in Fizeau's determination of flow rate. Michelson redesigned Fizeau's apparatus with larger diameter tubes and a large reservoir providing three minutes of steady water flow. His common path interferometer design provided automatic compensation of path length, so that white light fringes were visible at once as soon as the optical elements were aligned. Topologically, the light path was that of a Sagnac interferometer with an even number of reflections in each light path.^{[S 6]} This offered extremely stable fringes that were, to first order, completely insensitive to any movement of its optical components. The stability was such that it was possible for him to insert a glass plate at h or even to hold a lighted match in the light path without displacing the center of the fringe system. Using this apparatus, Michelson and Morley were able to completely confirm Fizeau's results.

Other experiments were conducted by Pieter Zeeman in 1914–1915. Using a scaled-up version of Michelson's apparatus connected directly to Amsterdam's main water conduit, Zeeman was able to perform extended measurements using monochromatic light ranging from violet (4358 Å) through red (6870 Å) to confirm Lorentz's modified coefficient.^{[P 4]}^{[P 5]} In 1910, Franz Harress used a rotating device and overall confirmed Fresnel's dragging coefficient. However, he additionally found a "systematic bias" in the data, which later turned out to be the Sagnac effect.^{[S 7]}

Since then, many experiments have been conducted measuring such dragging coefficients, often in combination with the Sagnac effect.^{[S 8]} For instance, in experiments using ring lasers together with rotating disks,^{[P 6]}^{[P 7]}^{[P 8]}^{[P 9]} or in neutron interferometric experiments.^{[P 10]}^{[P 11]}^{[P 12]} Also a transverse dragging effect was observed, i.e. when the medium is moving at right angles to the direction of the incident light.^{[P 13]}^{[P 14]}

Hoek experiment

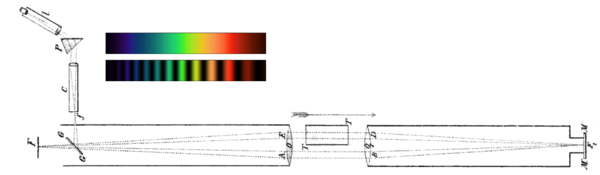
An indirect confirmation of Fresnel's dragging coefficient was provided by Martin Hoek (1868).^{[P 15]}^{[S 9]} His apparatus was similar to Fizeau's, though in his version only one arm contained an area filled with resting water, while the other arm was in the air. As seen by an observer resting in the aether, Earth and hence the water is in motion. So the following travel times of two light rays traveling in opposite direction were calculated by Hoek (neglecting the transverse direction, see image):

$t_{1} = \frac{A B}{c + v} + \frac{D E}{\frac{c}{n} - v}$

$t_{2} = \frac{A B}{c - v} + \frac{D E}{\frac{c}{n} + v}$

The travel times are not the same, which should be indicated by an interference shift. However, if Fresnel's dragging coefficient is applied to the water in the aether frame, the travel time difference (to first order in v/c) vanishes. Using different setups Hoek actually obtained a null result, confirming Fresnel's dragging coefficient. (For a similar experiment refuting the possibility of shielding the aether wind, see Hammar experiment).

In the particular version of the experiment shown here, Hoek used a prism P to disperse light from a slit into a spectrum which passed through a collimator C before entering the apparatus. With the apparatus oriented parallel to the hypothetical aether wind, Hoek expected the light in one circuit to be retarded 7/600 mm with respect to the other. Where this retardation represented an integral number of wavelengths, he expected to see constructive interference; where this retardation represented a half-integral number of wavelengths, he expected to see destructive interference. In the absence of dragging, his expectation was for the observed spectrum to be continuous with the apparatus oriented transversely to the aether wind, and to be banded with the apparatus oriented parallel to the aether wind. His actual experimental results were completely negative.

Controversy

Although Fresnel's hypothesis was empirically successful in explaining Fizeau's results, many leading experts in the field, including Fizeau (1851), Éleuthère Mascart (1872), Ketteler (1873), Veltmann (1873), and Lorentz (1886) were united in considering Fresnel's partial aether-dragging hypothesis to be on shaky theoretical grounds. For example, Veltmann (1870) demonstrated that Fresnel's formula implies that the aether would have to be dragged by different amounts for different colors of light, since the index of refraction depends on wavelength; Mascart (1872) demonstrated a similar result for polarized light traveling through a birefringent medium. In other words, the aether must be capable of sustaining different motions at the same time.^{[S 10]}

Fizeau's dissatisfaction with the result of his own experiment is easily discerned in the conclusion to his report:

The success of the experiment seems to me to render the adoption of Fresnel's hypothesis necessary, or at least the law which he found for the expression of the alteration of the velocity of light by the effect of motion of a body; for although that law being found true may be a very strong proof in favour of the hypothesis of which it is only a consequence, perhaps the conception of Fresnel may appear so extraordinary, and in some respects so difficult, to admit, that other proofs and a profound examination on the part of geometricians will still be necessary before adopting it as an expression of the real facts of the case.^{[P 1]}

Despite the dissatisfaction of most physicists with Fresnel's partial aether-dragging hypothesis, repetitions and improvements to his experiment (see section above) by others confirmed his results to high accuracy.

Besides the problems of the partial aether-dragging hypothesis, another major problem arose with the Michelson-Morley experiment (1887). In Fresnel's theory, the aether is almost stationary, so the experiment should have given a positive result. However, the result of this experiment was negative. Thus from the viewpoint of the aether models at that time, the experimental situation was contradictory: On one hand, the Aberration of light, the Fizeau experiment and the repetition by Michelson and Morley in 1886 appeared to prove the (almost) stationary aether with partial aether-dragging. On the other hand, the Michelson-Morley experiment of 1887 appeared to prove that the aether is at rest with respect to Earth, apparently supporting the idea of complete aether-dragging (see aether drag hypothesis).^{[S 2]} So the very success of Fresnel's hypothesis in explaining Fizeau's results helped lead to a theoretical crisis, which was not resolved until the development of the theory of special relativity.^{[S 10]}

Lorentz's interpretation

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. In 1892, Hendrik Lorentz proposed a modification of Fresnel's model, in which the aether is completely stationary. He succeeded in deriving Fresnel's dragging coefficient by the reaction of the moving water upon the interfering waves, without the need of any aether entrainment.^{[S 1]}^{[S 2]} He also discovered that the transition from one to another reference frame could be simplified by using an auxiliary time variable which he called local time:

t^{'} = t - \frac{v x}{c^{2}}

In 1895, Lorentz more generally explained Fresnel's coefficient based on the concept of local time. However, Lorentz's theory had the same fundamental problem as Fresnel's: a stationary aether contradicted the Michelson-Morley experiment. So in 1892 Lorentz proposed that moving bodies contract in the direction of motion (FitzGerald-Lorentz contraction hypothesis, since George FitzGerald had already arrived in 1889 at this conclusion).^{[S 1]}^{[S 2]} The equations that he used to describe these effects were further developed by him until 1904. These are now called the Lorentz transformations in his honor, and are identical in form to the equations that Einstein were later to derive from first principles. Unlike Einstein's equations, however, Lorentz's transformations were strictly ad hoc, their only justification being that they seemed to work.

Derivation in special relativity

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. Einstein showed how Lorentz's equations could be derived as the logical outcome of a set of two simple starting postulates. In addition Einstein recognized that the stationary aether concept has no place in special relativity, and that the Lorentz transformation concerns the nature of space and time. Together with the moving magnet and conductor problem, the negative aether drift experiments, and the aberration of light, the Fizeau experiment was one of the key experimental results that shaped Einstein's thinking about relativity.^{[S 11]} Robert S. Shankland reported some conversations with Einstein, in which Einstein emphasized the importance of the Fizeau experiment:^{[S 12]}

31 year-old Systems Analyst Bud from Deep River, spends time with pursuits for instance r/c cars, property developers new condo in singapore singapore and books. Last month just traveled to Orkhon Valley Cultural Landscape.

Max von Laue (1907) demonstrated that the Fresnel drag coefficient can be easily explained as a natural consequence of the relativistic formula for addition of velocities,^{[S 13]} namely:

The speed of light in immobile water is c/n.

From the velocity composition law it follows that the speed of light observed in the laboratory, where water is flowing with speed v (in the same direction as light) is

V_{L A B} = \frac{\frac{c}{n} + v}{1 + \frac{\frac{c}{n} v}{c^{2}}} = \frac{\frac{c}{n} + v}{1 + \frac{v}{c n}}

Thus the difference in speed is (assuming v is small comparing to c, approximating to the first non-trivial correction)

V_{L A B} - \frac{c}{n} = \frac{\frac{c}{n} + v}{1 + \frac{v}{c n}} - \frac{c}{n} = \frac{\frac{c}{n} + v - \frac{c}{n} (1 + \frac{v}{c n})}{1 + \frac{v}{c n}}

= \frac{v (1 - \frac{1}{n^{2}})}{1 + \frac{v}{c n}} \approx v (1 - \frac{1}{n^{2}})

This is accurate when v/c << 1, and agrees with the formula based upon Fizeau's measurements, which satisfied the condition v/c << 1.

Fizeau's experiment is hence supporting evidence for the collinear case of Einstein's velocity addition formula.^{[P 16]}

References

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.

Secondary sources

↑ ^1.0 ^1.1 ^1.2 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
↑ ^2.0 ^2.1 ^2.2 ^2.3 Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.

Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.

In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.

Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region

Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.

15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.

To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang; see pp. 631-634, and references therein.
↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
↑ ^10.0 ^10.1 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
↑ Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.

Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.

In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.

Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region

Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.

15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.

To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534

Primary sources

↑ ^1.0 ^1.1 One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
English: One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
English: One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
↑ Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.

Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.

In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.

Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region

Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.

15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.

To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010

Template:Tests of special relativity

[mil-3] 1.0 ^1.1 ^1.2 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534

[jan-4] 2.0 ^2.1 ^2.2 ^2.3 Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.

Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.

In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.

Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region

Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.

15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.

To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010

[lah-5] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[Wood-6] 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534

[paul-7] 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534

[Hariharan2007-9] 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534

[and-12] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[sted-13] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang; see pp. 631-634, and references therein.

[ferr-24] 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534

[Stachel2005-25] 10.0 ^10.1 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534

[norton-26] Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.

Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.

In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.

Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region

Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.

15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.

To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010

[shank-27] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[Mermin-28] 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

My blog: http://www.primaboinca.com/view_profile.php?userid=5889534

[fiz1-1] 1.0 ^1.1 One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
English: One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[fiz2-2] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang
English: One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[mich-8] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[zee1-10] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[zee2-11] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[macek-14] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[bilger1-15] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[bilger2-16] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[sanders-17] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[klein-18] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[bonse-19] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[arif-20] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[jones1-21] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[jones2-22] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[hoek-23] One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting

In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang

Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules

Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.

A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running

The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more

There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang

[laue-29] Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.

Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.

In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.

Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region

Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.

15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.

To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010

[P 1]

[P 2]

[S 1]

[S 2]

[S 3]

[S 4]

[S 5]

[P 3]

[S 6]

[P 4]

[P 5]

[S 7]

[S 8]

[P 6]

[P 7]

[P 8]

[P 9]

[P 10]

[P 11]

[P 12]

[P 13]

[P 14]

[P 15]

[S 9]

[S 10]

[S 11]

[S 12]

[S 13]

[P 16]

Torsion-free abelian group

Contents

Experimental setup

Fresnel drag coefficient

Repetitions

Hoek experiment

Controversy

Lorentz's interpretation

Derivation in special relativity

See also

References

Navigation menu

Torsion-free abelian group

Experimental setup

Fresnel drag coefficient

Repetitions

Hoek experiment

Controversy

Lorentz's interpretation

Derivation in special relativity

See also

References

Navigation menu

Search