Principal–agent problem: Difference between revisions
en>Hires an editor m small edits |
en>Trivialist {{multiple issues}} Copyedit (minor) |
||
| Line 1: | Line 1: | ||
{{Summarize|to|Optics|date=June 2009}} | |||
'''Geometrical optics''', or '''ray optics''', describes [[light]] [[Wave propagation|propagation]] in terms of "[[ray (optics)|rays]]". The "ray" in geometric optics is an [[abstract object|abstraction]], or "[[instrumentalism|instrument]]", which can be used to approximately model how light will propagate. Light rays are defined to propagate in a rectilinear path as they travel in a homogeneous medium. Rays bend (and may split in two) at the [[wiktionary:interface|interface]] between two dissimilar [[optical medium|media]], may curve in a medium where the [[refractive index]] changes, and may be absorbed and reflected. Geometrical optics provides rules, which may depend on the color (wavelength) of the ray, for propagating these rays through an optical system. This is a significant simplification of optics that fails to account for optical effects such as [[diffraction]] and [[Interference (wave propagation)|interference]]. It is an excellent approximation, however, when the wavelength is very small compared with the size of structures with which the light interacts. Geometric optics can be used to describe the geometrical aspects of [[Image|imaging]], including [[optical aberration]]s. | |||
==Explanation== | |||
[[Image:Plane wave wavefronts 3D.svg|thumb|right|As light travels through space, it [[oscillation|oscillates]] in [[amplitude]]. In this image, each maximum amplitude [[crest (physics)|crest]] is marked with a [[plane (geometry)|plane]] to illustrate the [[wavefront]]. The [[ray (optics)|ray]] is the arrow [[perpendicular]] to these [[parallel (geometry)|parallel]] surfaces.]] | |||
A light ray is a [[Line (geometry)|line]] or [[curve]] that is [[perpendicular]] to the light's [[wavefront]]s (and is therefore [[wiktionary:collinear|collinear]] with the [[wave vector]]). | |||
A slightly more rigorous definition of a light ray follows from [[Fermat's principle]], which states that the path taken between two points by a ray of light is the path that can be traversed in the least time.<ref>Arthur Schuster, ''An Introduction to the Theory of Optics'', London: Edward Arnold, 1904 [http://books.google.com/books?vid=OCLC03146755&id=X0AcBd-bcCwC&pg=PA41&lpg=PA41&dq=fermat%27s-principle online].</ref> | |||
Geometrical optics is often simplified by making the [[paraxial approximation]], or "small angle approximation." The mathematical behavior then becomes [[Linear system|linear]], allowing optical components and systems to be described by simple matrices. This leads to the techniques of [[Gaussian optics]] and ''paraxial [[ray tracing (physics)|ray tracing]]'', which are used to find basic properties of optical systems, such as approximate [[image]] and object positions and [[magnification]]s.<ref name=Greivenkamp>{{cite isbn|0819452947|pages=19–20}}</ref> | |||
==Reflection== | |||
{{main|Reflection (physics)}} | |||
[[Image:Reflection angles.svg|frame|Diagram of [[specular reflection]]]] | |||
Glossy surfaces such as [[mirror]]s reflect light in a simple, predictable way. This allows for production of reflected images that can be associated with an actual ([[real image|real]]) or extrapolated ([[virtual image|virtual]]) location in space. | |||
With such surfaces, the direction of the reflected ray is determined by the angle the incident ray makes with the [[surface normal]], a line perpendicular to the surface at the point where the ray hits. The incident and reflected rays lie in a single plane, and the angle between the reflected ray and the surface normal is the same as that between the incident ray and the normal.<ref name=Geoptics>{{cite book|title=University Physics 8e|author=Hugh D. Young|publisher=Addison-Wesley|date=1992|isbn=0-201-52981-5}}Chapter 35</ref> This is known as the [[Law of Reflection]]. | |||
For [[Plane mirror|flat mirrors]], the law of reflection implies that images of objects are upright and the same distance behind the mirror as the objects are in front of the mirror. The image size is the same as the object size. (The [[magnification]] of a flat mirror is equal to one.) The law also implies that [[mirror image]]s are [[Parity (physics)|parity inverted]], which is perceived as a left-right inversion. | |||
[[Curved mirror|Mirrors with curved surfaces]] can be modeled by [[ray tracing (physics)|ray tracing]] and using the law of reflection at each point on the surface. For [[Parabolic reflector|mirrors with parabolic surfaces]], parallel rays incident on the mirror produce reflected rays that converge at a common [[focus (optics)|focus]]. Other curved surfaces may also focus light, but with aberrations due to the diverging shape causing the focus to be smeared out in space. In particular, spherical mirrors exhibit [[spherical aberration]]. Curved mirrors can form images with magnification greater than or less than one, and the image can be upright or inverted. An upright image formed by reflection in a mirror is always virtual, while an inverted image is real and can be projected onto a screen.<ref name=Geoptics /> | |||
==Refraction== | |||
{{Summarize|date=June 2009}} | |||
{{main|Refraction}} | |||
[[Image:Snells law.svg|thumb|300px|Illustration of Snell's Law]] | |||
Refraction occurs when light travels through an area of space that has a changing index of refraction. The simplest case of refraction occurs when there is an interface between a uniform medium with index of refraction <math>n_1</math> and another medium with index of refraction <math>n_2</math>. In such situations, [[Snell's Law]] describes the resulting deflection of the light ray: | |||
:<math>n_1\sin\theta_1 = n_2\sin\theta_2\ </math> | |||
where <math>\theta_1</math> and <math>\theta_2</math> are the angles between the normal (to the interface) and the incident and refracted waves, respectively. This phenomenon is also associated with a changing speed of light as seen from the definition of index of refraction provided above which implies: | |||
:<math>v_1\sin\theta_2\ = v_2\sin\theta_1</math> | |||
where <math>v_1</math> and <math>v_2</math> are the wave velocities through the respective media.<ref name=Geoptics /> | |||
Various consequences of Snell's Law include the fact that for light rays traveling from a material with a high index of refraction to a material with a low index of refraction, it is possible for the interaction with the interface to result in zero transmission. This phenomenon is called [[total internal reflection]] and allows for [[fiber optics]] technology. As light signals travel down a fiber optic cable, it undergoes total internal reflection allowing for essentially no light lost over the length of the cable. It is also possible to produce [[plane polarization|polarized light rays]] using a combination of reflection and refraction: When a refracted ray and the reflected ray form a [[right angle]], the reflected ray has the property of "plane polarization". The angle of incidence required for such a scenario is known as [[Brewster's angle]].<ref name=Geoptics /> | |||
Snell's Law can be used to predict the deflection of light rays as they pass through "linear media" as long as the indexes of refraction and the geometry of the media are known. For example, the propagation of light through a [[prism (optics)|prism]] results in the light ray being deflected depending on the shape and orientation of the prism. Additionally, since different frequencies of light have slightly different indexes of refraction in most materials, refraction can be used to produce [[dispersion (optics)|dispersion]] [[spectrum|spectra]] that appear as rainbows. The discovery of this phenomenon when passing light through a prism is famously attributed to [[Isaac Newton]].<ref name=Geoptics /> | |||
Some media have an index of refraction which varies gradually with position and, thus, light rays curve through the medium rather than travel in straight lines. This effect is what is responsible for [[mirage]]s seen on hot days where the changing index of refraction of the air causes the light rays to bend creating the appearance of specular reflections in the distance (as if on the surface of a pool of water). Material that has a varying index of refraction is called a gradient-index (GRIN) material and has many useful properties used in modern optical scanning technologies including [[photocopiers]] and [[scanners]]. The phenomenon is studied in the field of [[gradient-index optics]].<ref>E. W. Marchand, Gradient Index Optics, New York, NY, Academic Press, 1978.</ref> | |||
[[Image:lens3b.svg|360px|thumb|A ray tracing diagram for a simple converging lens.]] | |||
A device which produces converging or diverging light rays due to refraction is known as a [[lens (optics)|lens]]. Thin lenses produce focal points on either side that can be modeled using the [[lensmaker's equation]].<ref name=hecht>{{cite book | first=Eugene|last=Hecht|year=1987|title=Optics|edition=2nd ed.|publisher=Addison Wesley|isbn=0-201-11609-X}} Chapters 5 & 6.</ref> In general, two types of lenses exist: [[convex lens]]es, which cause parallel light rays to converge, and [[concave lens]]es, which cause parallel light rays to diverge. The detailed prediction of how images are produced by these lenses can be made using ray-tracing similar to curved mirrors. Similarly to curved mirrors, thin lenses follow a simple equation that determines the location of the images given a particular focal length (<math>f</math>) and object distance (<math>S_1</math>): | |||
:<math>\frac{1}{S_1} + \frac{1}{S_2} = \frac{1}{f} </math> | |||
where <math>S_2</math> is the distance associated with the image and is considered by convention to be negative if on the same side of the lens as the object and positive if on the opposite side of the lens.<ref name=hecht /> The focal length f is considered negative for concave lenses. | |||
Incoming parallel rays are focused by a convex lens into an inverted real image one focal length from the lens, on the far side of the lens. Rays from an object at finite distance are focused further from the lens than the focal distance; the closer the object is to the lens, the further the image is from the lens. With concave lenses, incoming parallel rays diverge after going through the lens, in such a way that they seem to have originated at an upright virtual image one focal length from the lens, on the same side of the lens that the parallel rays are approaching on. Rays from an object at finite distance are associated with a virtual image that is closer to the lens than the focal length, and on the same side of the lens as the object. The closer the object is to the lens, the closer the virtual image is to the lens. | |||
Likewise, the magnification of a lens is given by | |||
:<math> M = - \frac{S_2}{S_1} = \frac{f}{f - S_1} </math> | |||
where the negative sign is given, by convention, to indicate an upright object for positive values and an inverted object for negative values. Similar to mirrors, upright images produced by single lenses are virtual while inverted images are real.<ref name=Geoptics /> | |||
Lenses suffer from [[optical aberration|aberrations]] that distort images and focal points. These are due to both to geometrical imperfections and due to the changing index of refraction for different wavelengths of light ([[chromatic aberration]]).<ref name=Geoptics /> | |||
==Underlying mathematics== | |||
{{section refimprove|date=August 2013}} | |||
{{Expert-subject|Mathematics|date=June 2009}}<!--The author neglected to define his variables..--> | |||
As a mathematical study, geometrical optics emerges as a short-[[wavelength]] limit for solutions to [[hyperbolic partial differential equation]]s. In this short-wavelength limit, it is possible to approximate the solution locally by | |||
:<math>u(t,x) \approx a(t,x)e^{i(k\cdot x - \omega t)}</math> | |||
where <math>k, \omega</math> satisfy a [[dispersion relation]], and the amplitude <math>a(t,x)</math> varies slowly. More precisely, the [[Leading-order term|leading order]] solution takes the form | |||
:<math>a_0(t,x) e^{i\varphi(t,x)/\varepsilon}.</math> | |||
The phase <math>\varphi(t,x)/\varepsilon</math> can be linearized to recover large wavenumber <math>k:= \nabla_x \varphi</math>, and frequency <math>\omega := -\partial_t \varphi</math>. The amplitude <math>a_0</math> satisfies a [[transport equation]]. The small parameter <math>\varepsilon\,</math> enters the scene due to highly oscillatory initial conditions. Thus, when initial conditions oscillate much faster than the coefficients of the differential equation, solutions will be highly oscillatory, and transported along rays. Assuming coefficients in the differential equation are smooth, the rays will be too. In other words, [[refraction]] does not take place. The motivation for this technique comes from studying the typical scenario of light propagation where short wavelength light travels along rays that minimize (more or less) its travel time. Its full application requires tools from [[microlocal analysis]]. | |||
===A simple example=== | |||
Starting with the wave equation for <math>(t,x) \in \mathbb{R}\times\mathbb{R}^n</math> | |||
:<math>L(\partial_t, \nabla_x) u := \left( \frac{\partial^2}{\partial t^2} - c(x)^2 \Delta \right)u(t,x) = 0, \;\; u(0,x) = u_0(x),\;\; u_t(0,x) = 0</math> | |||
assume an [[asymptotic]] series solution of the form | |||
:<math>u(t,x) \sim a_\varepsilon(t,x)e^{i\varphi(t,x)/\varepsilon} = \sum_{j=0}^\infty i^j \varepsilon^j a_j(t,x) e^{i\varphi(t,x)/\varepsilon}.</math> | |||
Check that | |||
:<math>L(\partial_t,\nabla_x)(e^{i\varphi(t,x)/\varepsilon}) a_\varepsilon(t,x) = e^{i\varphi(t,x)/\varepsilon} | |||
\left( \left(\frac{i}{\varepsilon} \right)^2 L(\varphi_t, \nabla_x\varphi)a_\varepsilon + \frac{2i}{\varepsilon} V(\partial_t,\nabla_x)a_\varepsilon + \frac{i}{\varepsilon} (a_\varepsilon L(\partial_t,\nabla_x)\varphi) + L(\partial_t,\nabla_x)a_\varepsilon \right)</math> | |||
with | |||
:<math>V(\partial_t,\nabla_x) := \frac{\partial \varphi}{\partial t} \frac{\partial}{\partial t} - c^2(x)\sum_j \frac{\partial \varphi}{\partial x_j} \frac{\partial}{\partial x_j}</math> | |||
Plugging the series into this equation, and equating powers of <math>\varepsilon</math>, the most singular term <math>O(\varepsilon^{-2})</math> satisfies the [[eikonal equation]] (in this case called a dispersion relation), | |||
:<math>0 = L(\varphi_t,\nabla_x\varphi) = (\varphi_t)^2 - c(x)^2(\nabla_x \varphi)^2.</math> | |||
To order <math>\varepsilon^{-1}</math>, the leading-order amplitude must satisfy a transport equation | |||
:<math>2V a_0 + (L\varphi)a_0 = 0 </math> | |||
With the definition <math>k : = \nabla_x \varphi</math>, <math>\omega := -\varphi_t</math>, the eikonal equation is precisely the dispersion relation that results by plugging the plane wave solution <math>e^{i(k\cdot x - \omega t)}</math> into the wave equation. The value of this more complicated expansion is that plane waves cannot be solutions when the wavespeed <math>c</math> is non-constant. However, it can be shown that the amplitude <math>a_0</math> and phase <math>\varphi</math> are smooth, so that on a local scale there are plane waves. | |||
To justify this technique, the remaining terms must be shown to be small in some sense. This can be done using energy estimates, and an assumption of rapidly oscillating initial conditions. It also must be shown that the series converges in some sense. | |||
==See also== | |||
* [[Hamiltonian optics]] | |||
==References== | |||
{{reflist}} | |||
==Further reading== | |||
* [[Robert Alfred Herman]] (1900) [http://archive.org/details/atreatiseongeom00hermgoog A Treatise on Geometrical optics] from [[Archive.org]]. | |||
*[http://www.wdl.org/en/item/2852 "The Light of the Eyes and the Enlightened Landscape of Vision"] is a manuscript, in Arabic, about geometrical optics, dating from the 16th century. | |||
*[http://books.google.com/books?id=TpY_AAAAYAAJ&pg=PA69#v=onepage&q&f=false Theory of Systems of Rays] - W.R. Hamilton in ''Transactions of the Royal Irish Academy'', Vol. XV, 1828. | |||
English translations of some early books and papers: | |||
*[http://neo-classical-physics.info/uploads/3/0/6/5/3065888/bruns_-_the_eikonal.pdf H. Bruns, "Das Eikonal"] | |||
*[http://neo-classical-physics.info/uploads/3/0/6/5/3065888/malus_-_optics.pdf M. Malus, "Optique"] | |||
*[http://neo-classical-physics.info/uploads/3/0/6/5/3065888/plucker_-_general_form_of_light_rays.pdf J. Plucker, "Discussion of the general form for light waves"] | |||
*[http://neo-classical-physics.info/uploads/3/0/6/5/3065888/kummer_-_rectilinear_ray_systems.pdf E. Kummer, "General theory of rectilinear ray systems"] | |||
*[http://neo-classical-physics.info/uploads/3/0/6/5/3065888/kummer_-_rectilinear_systems_of_light_rays.pdf E. Kummer, presentation on optically-realizable rectilinear ray systems] | |||
*[http://neo-classical-physics.info/uploads/3/0/6/5/3065888/meibauer_-_rectilinear_ray_systems.pdf R. Meibauer, "Theory of rectilinear systems of light rays"] | |||
*[http://neo-classical-physics.info/uploads/3/0/6/5/3065888/pasch_-_focal_and_singularity_surfaces.pdf M. Pasch, "On the focal surfaces of ray systems and the singularity surfaces of complexes"] | |||
*[http://neo-classical-physics.info/uploads/3/0/6/5/3065888/levistal_-_geometrical_optics.pdf A. Levistal, "Research in geometrical optics"] | |||
*[http://neo-classical-physics.info/uploads/3/0/6/5/3065888/klein_-_bruns_eikonal.pdf F. Klein, "On the Bruns eikonal"] | |||
*[http://neo-classical-physics.info/uploads/3/0/6/5/3065888/dontot_-_integral_invariants_and_geom._opt..pdf R. Dontot, "On integral invariants and some points of geometrical optics"] | |||
*[http://neo-classical-physics.info/uploads/3/0/6/5/3065888/de_donder_-_int._inv._in_optics.pdf T. de Donder, "On the integral invariants of optics"] | |||
==External links== | |||
*[http://spie.org/Documents/Publications/00%20STEP%20Module%2003.pdf Fundamentals of Photonics - Module on Basic Geometrical Optics] | |||
[[Category:Geometrical optics]] | |||
Revision as of 17:04, 21 October 2013
Template:Summarize Geometrical optics, or ray optics, describes light propagation in terms of "rays". The "ray" in geometric optics is an abstraction, or "instrument", which can be used to approximately model how light will propagate. Light rays are defined to propagate in a rectilinear path as they travel in a homogeneous medium. Rays bend (and may split in two) at the interface between two dissimilar media, may curve in a medium where the refractive index changes, and may be absorbed and reflected. Geometrical optics provides rules, which may depend on the color (wavelength) of the ray, for propagating these rays through an optical system. This is a significant simplification of optics that fails to account for optical effects such as diffraction and interference. It is an excellent approximation, however, when the wavelength is very small compared with the size of structures with which the light interacts. Geometric optics can be used to describe the geometrical aspects of imaging, including optical aberrations.
Explanation

A light ray is a line or curve that is perpendicular to the light's wavefronts (and is therefore collinear with the wave vector).
A slightly more rigorous definition of a light ray follows from Fermat's principle, which states that the path taken between two points by a ray of light is the path that can be traversed in the least time.[1]
Geometrical optics is often simplified by making the paraxial approximation, or "small angle approximation." The mathematical behavior then becomes linear, allowing optical components and systems to be described by simple matrices. This leads to the techniques of Gaussian optics and paraxial ray tracing, which are used to find basic properties of optical systems, such as approximate image and object positions and magnifications.[2]
Reflection
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

Glossy surfaces such as mirrors reflect light in a simple, predictable way. This allows for production of reflected images that can be associated with an actual (real) or extrapolated (virtual) location in space.
With such surfaces, the direction of the reflected ray is determined by the angle the incident ray makes with the surface normal, a line perpendicular to the surface at the point where the ray hits. The incident and reflected rays lie in a single plane, and the angle between the reflected ray and the surface normal is the same as that between the incident ray and the normal.[3] This is known as the Law of Reflection.
For flat mirrors, the law of reflection implies that images of objects are upright and the same distance behind the mirror as the objects are in front of the mirror. The image size is the same as the object size. (The magnification of a flat mirror is equal to one.) The law also implies that mirror images are parity inverted, which is perceived as a left-right inversion.
Mirrors with curved surfaces can be modeled by ray tracing and using the law of reflection at each point on the surface. For mirrors with parabolic surfaces, parallel rays incident on the mirror produce reflected rays that converge at a common focus. Other curved surfaces may also focus light, but with aberrations due to the diverging shape causing the focus to be smeared out in space. In particular, spherical mirrors exhibit spherical aberration. Curved mirrors can form images with magnification greater than or less than one, and the image can be upright or inverted. An upright image formed by reflection in a mirror is always virtual, while an inverted image is real and can be projected onto a screen.[3]
Refraction
Template:Summarize Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
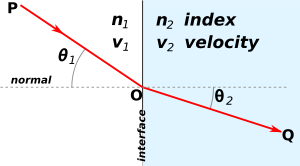
Refraction occurs when light travels through an area of space that has a changing index of refraction. The simplest case of refraction occurs when there is an interface between a uniform medium with index of refraction and another medium with index of refraction . In such situations, Snell's Law describes the resulting deflection of the light ray:
where and are the angles between the normal (to the interface) and the incident and refracted waves, respectively. This phenomenon is also associated with a changing speed of light as seen from the definition of index of refraction provided above which implies:
where and are the wave velocities through the respective media.[3]
Various consequences of Snell's Law include the fact that for light rays traveling from a material with a high index of refraction to a material with a low index of refraction, it is possible for the interaction with the interface to result in zero transmission. This phenomenon is called total internal reflection and allows for fiber optics technology. As light signals travel down a fiber optic cable, it undergoes total internal reflection allowing for essentially no light lost over the length of the cable. It is also possible to produce polarized light rays using a combination of reflection and refraction: When a refracted ray and the reflected ray form a right angle, the reflected ray has the property of "plane polarization". The angle of incidence required for such a scenario is known as Brewster's angle.[3]
Snell's Law can be used to predict the deflection of light rays as they pass through "linear media" as long as the indexes of refraction and the geometry of the media are known. For example, the propagation of light through a prism results in the light ray being deflected depending on the shape and orientation of the prism. Additionally, since different frequencies of light have slightly different indexes of refraction in most materials, refraction can be used to produce dispersion spectra that appear as rainbows. The discovery of this phenomenon when passing light through a prism is famously attributed to Isaac Newton.[3]
Some media have an index of refraction which varies gradually with position and, thus, light rays curve through the medium rather than travel in straight lines. This effect is what is responsible for mirages seen on hot days where the changing index of refraction of the air causes the light rays to bend creating the appearance of specular reflections in the distance (as if on the surface of a pool of water). Material that has a varying index of refraction is called a gradient-index (GRIN) material and has many useful properties used in modern optical scanning technologies including photocopiers and scanners. The phenomenon is studied in the field of gradient-index optics.[4]

A device which produces converging or diverging light rays due to refraction is known as a lens. Thin lenses produce focal points on either side that can be modeled using the lensmaker's equation.[5] In general, two types of lenses exist: convex lenses, which cause parallel light rays to converge, and concave lenses, which cause parallel light rays to diverge. The detailed prediction of how images are produced by these lenses can be made using ray-tracing similar to curved mirrors. Similarly to curved mirrors, thin lenses follow a simple equation that determines the location of the images given a particular focal length () and object distance ():
where is the distance associated with the image and is considered by convention to be negative if on the same side of the lens as the object and positive if on the opposite side of the lens.[5] The focal length f is considered negative for concave lenses.
Incoming parallel rays are focused by a convex lens into an inverted real image one focal length from the lens, on the far side of the lens. Rays from an object at finite distance are focused further from the lens than the focal distance; the closer the object is to the lens, the further the image is from the lens. With concave lenses, incoming parallel rays diverge after going through the lens, in such a way that they seem to have originated at an upright virtual image one focal length from the lens, on the same side of the lens that the parallel rays are approaching on. Rays from an object at finite distance are associated with a virtual image that is closer to the lens than the focal length, and on the same side of the lens as the object. The closer the object is to the lens, the closer the virtual image is to the lens.
Likewise, the magnification of a lens is given by
where the negative sign is given, by convention, to indicate an upright object for positive values and an inverted object for negative values. Similar to mirrors, upright images produced by single lenses are virtual while inverted images are real.[3]
Lenses suffer from aberrations that distort images and focal points. These are due to both to geometrical imperfections and due to the changing index of refraction for different wavelengths of light (chromatic aberration).[3]
Underlying mathematics
Template:Section refimprove Template:Expert-subject As a mathematical study, geometrical optics emerges as a short-wavelength limit for solutions to hyperbolic partial differential equations. In this short-wavelength limit, it is possible to approximate the solution locally by
where satisfy a dispersion relation, and the amplitude varies slowly. More precisely, the leading order solution takes the form
The phase can be linearized to recover large wavenumber , and frequency . The amplitude satisfies a transport equation. The small parameter enters the scene due to highly oscillatory initial conditions. Thus, when initial conditions oscillate much faster than the coefficients of the differential equation, solutions will be highly oscillatory, and transported along rays. Assuming coefficients in the differential equation are smooth, the rays will be too. In other words, refraction does not take place. The motivation for this technique comes from studying the typical scenario of light propagation where short wavelength light travels along rays that minimize (more or less) its travel time. Its full application requires tools from microlocal analysis.
A simple example
Starting with the wave equation for
assume an asymptotic series solution of the form
Check that
with
Plugging the series into this equation, and equating powers of , the most singular term satisfies the eikonal equation (in this case called a dispersion relation),
To order , the leading-order amplitude must satisfy a transport equation
With the definition , , the eikonal equation is precisely the dispersion relation that results by plugging the plane wave solution into the wave equation. The value of this more complicated expansion is that plane waves cannot be solutions when the wavespeed is non-constant. However, it can be shown that the amplitude and phase are smooth, so that on a local scale there are plane waves.
To justify this technique, the remaining terms must be shown to be small in some sense. This can be done using energy estimates, and an assumption of rapidly oscillating initial conditions. It also must be shown that the series converges in some sense.
See also
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
Further reading
- Robert Alfred Herman (1900) A Treatise on Geometrical optics from Archive.org.
- "The Light of the Eyes and the Enlightened Landscape of Vision" is a manuscript, in Arabic, about geometrical optics, dating from the 16th century.
- Theory of Systems of Rays - W.R. Hamilton in Transactions of the Royal Irish Academy, Vol. XV, 1828.
English translations of some early books and papers:
- H. Bruns, "Das Eikonal"
- M. Malus, "Optique"
- J. Plucker, "Discussion of the general form for light waves"
- E. Kummer, "General theory of rectilinear ray systems"
- E. Kummer, presentation on optically-realizable rectilinear ray systems
- R. Meibauer, "Theory of rectilinear systems of light rays"
- M. Pasch, "On the focal surfaces of ray systems and the singularity surfaces of complexes"
- A. Levistal, "Research in geometrical optics"
- F. Klein, "On the Bruns eikonal"
- R. Dontot, "On integral invariants and some points of geometrical optics"
- T. de Donder, "On the integral invariants of optics"
External links
- ↑ Arthur Schuster, An Introduction to the Theory of Optics, London: Edward Arnold, 1904 online.
- ↑ Template:Cite isbn
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534Chapter 35 - ↑ E. W. Marchand, Gradient Index Optics, New York, NY, Academic Press, 1978.
- ↑ 5.0 5.1 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 Chapters 5 & 6.



































