Exponential function: Difference between revisions
en>JYBot m r2.7.1) (Robot: Adding af:Eksponensiële funksie |
en>Favonian m Reverted edits by 97.77.222.122 (talk) to last version by ClueBot NG |
||
| Line 1: | Line 1: | ||
{{About|the function ''e''<sup>''x''</sup>|exponentially increasing functions of the more general form ''cb''<sup>''x''</sup>|Exponential growth}} | |||
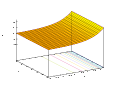
[[Image:exp.svg|thumb|200px|right|The natural exponential function <math>y = e^x</math>]] | |||
In [[mathematics]], the '''exponential function''' is the [[function (mathematics)|function]] ''e''<sup>''x''</sup>, where ''[[E (mathematical constant)|e]]'' is the number (approximately 2.718281828) such that the function ''e''<sup>''x''</sup> is its own [[derivative]].<ref>Goldstein, Lay, Schneider, Asmar, ''Brief calculus and its applications'', 11th ed., Prentice-Hall, 2006.</ref><ref>"''The natural exponential function is identical with its derivative.'' This is really the source of all the properties of the exponential function, and the basic reason for its importance in applications…" - p.448 of Courant and Robbins, ''What is mathematics? An elementary approach to ideas and methods'' (edited by Stewart), 2nd revised edition, Oxford Univ. Press, 1996.</ref> The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change (i.e. percentage increase or decrease) in the dependent variable. The function is often written as exp(''x''), especially when it is impractical to write the independent variable as a [[superscript]]. The exponential function is widely used in [[physics]], [[chemistry]], [[engineering]], [[mathematical biology]], [[economics]] and mathematics. | |||
{| class=infobox width=200px | |||
|+ Exponential function | |||
|- | |||
| '''Representation''' || <math>e^x \,</math> | |||
|- | |||
| '''Inverse''' || <math>\ln x \,</math> | |||
|- | |||
| '''Derivative''' || <math>e^x \,</math> | |||
|- | |||
| '''Indefinite Integral''' || <math>e^x + C \,</math> | |||
|} | |||
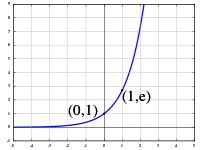
The [[graph of a function|graph]] of ''y'' = ''e''<sup>''x''</sup> is upward-sloping, and increases faster as ''x'' increases. The graph always lies above the ''x''-axis but can get arbitrarily close to it for negative ''x''; thus, the ''x''-axis is a horizontal [[asymptote]]. The [[slope]] of the [[tangent]] to the graph at each point is equal to its ''y'' coordinate at that point. The [[inverse function]] is the [[natural logarithm]] ln(''x''); because of this, some old texts<ref>"Inverse Use of a Table of Logarithms; that is, given a logarithm, to find the number corresponding to it, (called its antilogarithm)…" - p.12 of Converse and Durrell, ''Plane and spherical trigonometry'', C.E. Merrill co., 1911.</ref> refer to the exponential function as the antilogarithm. | |||
Sometimes the term exponential function is used more generally for functions of the form ''cb''<sup>''x''</sup>, where the [[base (exponentiation)|base]] ''b'' is any positive [[real number]], not necessarily ''e''. See [[exponential growth]] for this usage. | |||
In general, the [[variable (mathematics)|variable]] ''x'' can be any real or [[complex number]] or even an entirely different kind of [[mathematical object]]; see the [[#Formal definition|formal definition below]]. | |||
{{E (mathematical constant)}} | |||
==Formal definition== | |||
{{main|Characterizations of the exponential function}} | |||
[[Image:Exp series.gif|right|thumb|The exponential function (in blue), and the sum of the first ''n'' + 1 terms of the power series on the left (in red).]] | |||
The exponential function e<sup>''x''</sup> can be characterized in a variety of equivalent ways. In particular it may be defined by the following [[power series]]:<ref name="rudin">Walter Rudin, Real and Complex Analysis, McGraw-Hill, 3rd ed., 1986, ISBN 978-0-07-054234-1, page 1</ref> | |||
: <math>e^x = \sum_{n = 0}^{\infty} {x^n \over n!} = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots</math> | |||
Using an alternate definition for the exponential function leads to the same result when expanded as a [[Taylor series]]. | |||
Less commonly, ''e''<sup>''x''</sup> is defined as the solution ''y'' to the equation | |||
: <math>x = \int_1^y {dt \over t}</math> | |||
It is also the following limit: | |||
: <math>e^x = \lim_{n \rightarrow \infty} \left(1 + \frac{x}{n}\right)^n</math> | |||
==Overview== | |||
The exponential function arises whenever a quantity [[exponential growth|grows]] or [[exponential decay|decays]] at a rate [[Proportionality (mathematics)|proportional]] to its current value. One such situation is [[continuously compounded interest]], and in fact it was this that led [[Jacob Bernoulli]] in 1683<ref name="mactutor">{{cite web |url=http://www-history.mcs.st-andrews.ac.uk/HistTopics/e.html |title=The number e |author=John J O'Connor; Edmund F Robertson |publisher=University of St Andrews, Scotland |work=School of Mathematics and Statistics |accessdate=2011-06-13}}</ref> to the number | |||
:<math>\lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n</math> | |||
now known as ''e''. Later, in 1697, [[Johann Bernoulli]] studied the calculus of the exponential function.<ref name="mactutor" /> | |||
If a principal amount of 1 earns interest at an annual rate of ''x'' compounded monthly, then the interest earned each month is ''x''/12 times the current value, so each month the total value is multiplied by (1+''x''/12), and the value at the end of the year is (1+''x''/12)<sup>12</sup>. If instead interest is compounded daily, this becomes (1+''x''/365)<sup>365</sup>. Letting the number of time intervals per year grow without bound leads to the [[limit of a function|limit]] definition of the exponential function, | |||
:<math>\exp(x) = \lim_{n\to\infty}\left(1 + \frac{x}{n}\right)^{n}</math> | |||
first given by [[Euler]].<ref>[[Eli Maor]], ''e: the Story of a Number'', p.156.</ref> | |||
This is one of a number of [[characterizations of the exponential function]]; others involve [[series (mathematics)|series]] or [[differential equation]]s. | |||
From any of these definitions it can be shown that the exponential function obeys the basic [[exponentiation]] identity, | |||
:<math>\exp(x + y) = \exp(x) \cdot \exp(y)</math> | |||
which is why it can be written as ''e''<sup>''x''</sup>. | |||
The [[derivative]] (rate of change) of the exponential function is the exponential function itself. More generally, a function with a rate of change ''proportional'' to the function itself (rather than equal to it) is expressible in terms of the exponential function. This function property leads to exponential growth and exponential decay. | |||
The exponential function extends to an [[entire function]] on the [[complex plane]]. [[Euler's formula]] relates its values at purely imaginary arguments to [[trigonometric functions]]. The exponential function also has analogues for which the argument is a [[matrix exponential|matrix]], or even an element of a [[Banach algebra]] or a [[exponential map|Lie algebra]]. | |||
==Derivatives and differential equations== | |||
[[Image:Exp tangent.svg|thumb|250px|right| The derivative of the exponential function is equal to the value of the function. From any point <math>P</math> on the curve (blue), let a tangent line (red), and a vertical line (green) with height <math>h</math> be drawn, forming a right triangle with a base <math>b</math> on the <math>x</math>-axis. Since the slope of the red tangent line (the derivative) at <math>P</math> is equal to the ratio of the triangle's height to the triangle's base (rise over run), and the derivative is equal to the value of the function, <math>h</math> must be equal to the ratio of <math>h</math> to <math>b</math>. Therefore the base <math>b</math> must always be <math>1</math>.]] | |||
The importance of the exponential function in mathematics and the sciences stems mainly from properties of its [[derivative]]. In particular, | |||
: <math>{\operatorname{d} \over \operatorname{d}x} e^x = e^x</math> | |||
That is, ''e''<sup>''x''</sup> is its own [[derivative]] and hence is a simple example of a [[Pfaffian function]]. Functions of the form ''ce''<sup>''x''</sup> for constant ''c'' are the only functions with that property (by the [[Picard–Lindelöf theorem]]). Other ways of saying the same thing include: | |||
*The slope of the graph at any point is the height of the function at that point. | |||
*The rate of increase of the function at ''x'' is equal to the value of the function at ''x''. | |||
*The function solves the [[differential equation]] ''y'' ′ = ''y''. | |||
*exp is a [[fixed point (mathematics)|fixed point]] of derivative as a [[Functional (mathematics)|functional]]. | |||
If a variable's growth or decay rate is [[proportionality (mathematics)|proportional]] to its size—as is the case in unlimited population growth (see [[Malthusian catastrophe]]), continuously compounded [[interest]], or [[radioactive decay]]—then the variable can be written as a constant times an exponential function of time. Explicitly for any real constant ''k'', a function ''f'': '''R'''→'''R''' satisfies ''f''′ = ''kf'' if and only if ''f''(''x'') = ''ce''<sup>''kx''</sup> for some constant ''c''. | |||
Furthermore for any differentiable function ''f''(''x''), we find, by the [[chain rule]]: | |||
: <math>{\operatorname{d} \over \operatorname{d}x} e^{f(x)} = f'(x)e^{f(x)}</math> | |||
==Continued fractions for ''e''<sup>''x''</sup>== | |||
A [[continued fraction]] for ''e''<sup>''x''</sup> can be obtained via [[Euler's continued fraction formula|an identity of Euler]]: | |||
:<math> | |||
e^x = 1 + \cfrac{x}{1 - \cfrac{x}{x + 2 - \cfrac{2x}{x + 3 - \cfrac{3x}{x + 4 - \ddots}}}} | |||
</math> | |||
The following [[generalized continued fraction]] for ''e''<sup>''z''</sup> converges more quickly:<ref>[http://link.springer.com/content/pdf/bbm%3A978-94-91216-37-4%2F1 "A.2.2 The exponential function." L. Lorentzen and H. Waadeland, ''Continued Fractions'', Atlantis Studies in Mathematics, page 268.]</ref> | |||
:<math> | |||
e^z = 1 + \cfrac{2z}{2 - z + \cfrac{z^2}{6 + \cfrac{z^2}{10 + \cfrac{z^2}{14 + \ddots}}}} | |||
</math> | |||
or, by applying the substitution ''z'' = {{frac|''x''|''y''}}: | |||
:<math> | |||
e^\frac{x}{y} = 1 + \cfrac{2x}{2y - x + \cfrac{x^2} {6y + \cfrac{x^2} {10y + \cfrac{x^2} {14y + \ddots}}}} | |||
</math> | |||
with a special case for ''z'' = 2: | |||
:<math> | |||
e^2 = 1 + \cfrac{4}{0 + \cfrac{2^2}{6 + \cfrac{2^2}{10 + \cfrac{2^2}{14 + \ddots\,}}}} = 7 + \cfrac{2}{5 + \cfrac{1}{7 + \cfrac{1}{9 + \cfrac{1}{11 + \ddots\,}}}} | |||
</math> | |||
This formula also converges, though more slowly, for ''z'' > 2. For example: | |||
:<math> | |||
e^3 = 1 + \cfrac{6}{-1 + \cfrac{3^2}{6 + \cfrac{3^2}{10 + \cfrac{3^2}{14 + \ddots\,}}}} = 13 + \cfrac{54}{7 + \cfrac{9}{14 + \cfrac{9}{18 + \cfrac{9}{22 + \ddots\,}}}} | |||
</math> | |||
{{anchor|On the complex plane}}<!-- This section is linked from [[Complex plane]] --> | |||
==Complex plane== | |||
[[Image:Complex exp.jpg|thumb|right|Exponential function on the complex plane. The transition from dark to light colors shows that the magnitude of the exponential function is increasing to the right. The periodic horizontal bands indicate that the exponential function is [[periodic function|periodic]] in the [[imaginary part]] of its argument.]] | |||
As in the [[real number|real]] case, the exponential function can be defined on the [[complex plane]] in several equivalent forms. One such definition parallels the power series definition for real numbers, where the real variable is replaced by a complex one: | |||
: <math>e^z = \sum_{n = 0}^\infty\frac{z^n}{n!} </math> | |||
The exponential function is periodic with [[imaginary number|imaginary]] period <math>2 \pi i</math> and can be written as | |||
: <math>e^{a + bi} = e^a (\cos b + i \sin b)</math> | |||
where ''a'' and ''b'' are real values and on the right the real functions must be used if used as a definition<ref>{{cite book | last = Ahlfors | first = Lars V. | title = Complex analysis | publisher = McGraw-Hill Book Company, Inc. | year = 1953 | authorlink1=Lars_Ahlfors}}</ref> (see also [[Euler's formula]]). This formula connects the exponential function with the [[trigonometric function]]s and to the [[hyperbolic function]]s. | |||
When considered as a function defined on the complex plane, the exponential function retains the properties | |||
* <math>e^{z + w} = e^z e^w\,</math> | |||
* <math>e^0 = 1\,</math> | |||
* <math>e^z \ne 0</math> | |||
* <math>{\operatorname{d} \over \operatorname{d}z} e^z = e^z</math> | |||
* <math>\,(e^z)^n = e^{nz}, n \in \mathbb{Z}</math> | |||
for all ''z'' and ''w''. | |||
The exponential function is an [[entire function]] as it is [[holomorphic function|holomorphic]] over the whole complex plane. It takes on every complex number excepting 0 as value. This is an example of [[Picard theorem|Picard's little theorem]] that any non-constant entire function takes on every complex number as value with at most one value excepted. | |||
Extending the natural logarithm to complex arguments yields the [[complex logarithm]] log ''z'', which is a [[multi-valued function]]. | |||
We can then define a more general exponentiation: | |||
: <math>z^w = e^{w \log z}</math> | |||
for all complex numbers ''z'' and ''w''. This is also a multi-valued function, even when ''z'' is real. This distinction is problematic, as the multi-valued functions log ''z'' and ''z''<sup>''w''</sup> are easily confused with their single-valued equivalents when substituting a real number for ''z''. The rule about multiplying exponents for the case of positive real numbers must be modified in a multi-valued context: | |||
: <math>(e^z)^w \ne e^{z w}</math>, but rather <math>(e^z)^w = e^{(z + 2\pi i n) w}\,</math> multivalued over integers ''n'' | |||
See [[Exponentiation#Failure of power and logarithm identities|failure of power and logarithm identities]] for more about problems with combining powers. | |||
The exponential function maps any [[line (mathematics)|line]] in the complex plane to a [[logarithmic spiral]] in the complex plane with the center at the [[Origin (mathematics)|origin]]. Two special cases might be noted: when the original line is parallel to the real axis, the resulting spiral never closes in on itself; when the original line is parallel to the imaginary axis, the resulting spiral is a circle of some radius. | |||
<gallery caption="Plots of the exponential function on the complex plane"> | |||
Image:ExponentialAbs_real_SVG.svg| ''z'' = Re(''e''<sup>''x''+''iy''</sup>) | |||
Image:ExponentialAbs_image_SVG.svg| ''z'' = Im(''e''<sup>''x''+''iy''</sup>) | |||
Image:ExponentialAbs_SVG.svg| ''z'' = |''e''<sup>''x''+''iy''</sup>| | |||
</gallery> | |||
===Computation of ''a''<sup>''b''</sup> where both ''a'' and ''b'' are complex=== | |||
{{Main|Exponentiation}} | |||
Complex exponentiation ''a''<sup>''b''</sup> can be defined by converting ''a'' to polar coordinates and using the identity (''e''<sup>ln(''a'')</sup>)<sup>''b''</sup> = ''a''<sup>''b''</sup>: | |||
: <math>a^b = \left(re^{\theta i}\right)^b = \left(e^{\ln(r) + \theta i}\right)^b = e^{(\ln(r) + \theta i)b}</math> | |||
However, when ''b'' is not an integer, this function is [[multivalued function|multivalued]], because ''θ'' is not unique (see [[exponentiation#Failure of power and logarithm identities|failure of power and logarithm identities]]). | |||
==Matrices and Banach algebras== | |||
The power series definition of the exponential function makes sense for square [[matrix (mathematics)|matrices]] (for which the function is called the [[matrix exponential]]) and more generally in any [[Banach algebra]] ''B''. In this setting, ''e''<sup>0</sup> = 1, and ''e''<sup>''x''</sup> is invertible with inverse ''e''<sup>−''x''</sup> for any ''x'' in ''B''. If ''xy'' =''yx'', then ''e''<sup>''x''+''y''</sup> = ''e''<sup>''x''</sup>''e''<sup>''y''</sup>, but this identity can fail for noncommuting ''x'' and ''y''. | |||
Some alternative definitions lead to the same function. For instance, ''e''<sup>''x''</sup> can be defined as | |||
<math>\textstyle \lim_{n \to \infty} \left(1 + \frac{x}{n} \right)^n</math> | |||
Or ''e''<sup>''x''</sup> can be defined as ''f''(1), where ''f'': '''R'''→''B'' is the solution to the differential equation ''f''′(''t'') = ''xf''(''t'') with initial condition ''f''(0) = 1. | |||
==Lie algebras== | |||
Given a [[Lie group]] ''G'' and its associated [[Lie algebra]] <math>\mathfrak{g}</math>, the [[exponential map]] is a map <math>\mathfrak{g}\to G</math> satisfying similar properties. In fact, since '''R''' is the Lie algebra of the Lie group of all positive real numbers under multiplication, the ordinary exponential function for real arguments is a special case of the Lie algebra situation. Similarly, since the Lie group GL(''n'','''R''') of invertible ''n'' × ''n'' matrices has as Lie algebra M(''n'','''R'''), the space of all ''n'' × ''n'' matrices, the exponential function for square matrices is a special case of the Lie algebra exponential map. | |||
The identity exp(''x''+''y'') = exp(''x'')exp(''y'') can fail for Lie algebra elements ''x'' and ''y'' that do not commute; the [[Baker–Campbell–Hausdorff formula]] supplies the necessary correction terms. | |||
==Double exponential function== | |||
{{main|double exponential function}} | |||
The term '''''double exponential function''''' can have two meanings: | |||
*a function with two exponential terms, with different exponents such as e<sup>3x</sup> - e<sup>(4x-2)</sup> | |||
*a function ''f(x) = a<sup>a<sup>x</sup></sup>''; this [[Big O notation|grows even faster]] than an exponential function; for example, if ''a'' = 10: ''f''(−1) = 1.26, ''f''(0) = 10, ''f''(1) = 10<sup>10</sup>, ''f''(2) = 10<sup>100</sup> = [[googol]], …, ''f''(100) = [[googolplex]]. | |||
[[Factorial]]s grow faster than exponential functions, but slower than double-exponential functions. [[Fermat number]]s, generated by <math>\,F(m) = 2^{2^m} + 1</math> and [[double Mersenne number]]s generated by <math>\,MM(p) = 2^{2^p - 1} - 1</math> are examples of double exponential functions. | |||
==Similar properties of ''e'' and the function ''e''<sup>''z''</sup>== | |||
The function ''e''<sup>''z''</sup> is not in '''C'''(''z'') (i.e., is not the quotient of two polynomials with complex coefficients). | |||
For ''n'' distinct complex numbers {''a''<sub>1</sub>, …, ''a''<sub>''n''</sub>}, the set {''e''<sup>''a''<sub>1</sub>''z''</sup>, …, ''e''<sup>''a''<sub>''n''</sub>''z''</sup>} is linearly independent over '''C'''(''z''). | |||
The function ''e''<sup>''z''</sup> is [[transcendental function|transcendental]] over '''C'''(''z''). | |||
==See also== | |||
{{Portal|Mathematics}} | |||
*[[Carlitz exponential]] - a characteristic ''p'' analogue | |||
*[[Characterizations of the exponential function]] | |||
*[[e (mathematical constant)]] | |||
*[[Exponential decay]] | |||
*[[Exponential field]] | |||
*[[Exponential growth]] | |||
*[[Exponentiation]] | |||
*[[List of exponential topics]] | |||
*[[List of integrals of exponential functions]] | |||
*[[P-adic exponential function|''p''-adic exponential function]] | |||
*[[Padé table#An example .E2.80.93 the exponential function|Padé approximation]] can be used to approximate the exponential function by a fraction of polynomial functions. | |||
*[[Tetration]] | |||
==References== | |||
{{Reflist}} | |||
==External links== | |||
* {{springer|title=Exponential function|id=p/e036910}} | |||
* {{planetmath reference|id=6341|title=Complex exponential function}} | |||
* {{planetmath reference|id=9313|title=Derivative of exponential function}} | |||
* [http://sympl.org/book/examples/interactive-plots/derivative-exponential-function Derivative of exponential function interactive graph] | |||
* {{MathWorld|urlname= ExponentialFunction|title= Exponential Function}} | |||
* [http://www.efunda.com/math/taylor_series/exponential.cfm Taylor Series Expansions of Exponential Functions] at [http://www.efunda.com efunda.com] | |||
* [http://www-math.mit.edu/daimp/ComplexExponential.html Complex exponential interactive graphic] | |||
* [http://www.docstoc.com/docs/137048039/Derivative-of-exp(x%5En)-by-limit-definition, Derivative of exp(x^n) by limit definition] | |||
* [http://www.docstoc.com/docs/148557191/A-general-limit-for-exponentials, General exponential limit] | |||
{{DEFAULTSORT:Exponential Function}} | |||
[[Category:Elementary special functions]] | |||
[[Category:Analytic functions]] | |||
[[Category:Exponentials]] | |||
[[Category:Special hypergeometric functions]] | |||
[[Category:E (mathematical constant)]] | |||
Revision as of 22:31, 11 December 2013
29 yr old Orthopaedic Surgeon Grippo from Saint-Paul, spends time with interests including model railways, top property developers in singapore developers in singapore and dolls. Finished a cruise ship experience that included passing by Runic Stones and Church.
In mathematics, the exponential function is the function ex, where e is the number (approximately 2.718281828) such that the function ex is its own derivative.[1][2] The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change (i.e. percentage increase or decrease) in the dependent variable. The function is often written as exp(x), especially when it is impractical to write the independent variable as a superscript. The exponential function is widely used in physics, chemistry, engineering, mathematical biology, economics and mathematics.
| Representation | |
| Inverse | |
| Derivative | |
| Indefinite Integral |
The graph of y = ex is upward-sloping, and increases faster as x increases. The graph always lies above the x-axis but can get arbitrarily close to it for negative x; thus, the x-axis is a horizontal asymptote. The slope of the tangent to the graph at each point is equal to its y coordinate at that point. The inverse function is the natural logarithm ln(x); because of this, some old texts[3] refer to the exponential function as the antilogarithm.
Sometimes the term exponential function is used more generally for functions of the form cbx, where the base b is any positive real number, not necessarily e. See exponential growth for this usage.
In general, the variable x can be any real or complex number or even an entirely different kind of mathematical object; see the formal definition below.
Template:E (mathematical constant)
Formal definition
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

The exponential function ex can be characterized in a variety of equivalent ways. In particular it may be defined by the following power series:[4]
Using an alternate definition for the exponential function leads to the same result when expanded as a Taylor series.
Less commonly, ex is defined as the solution y to the equation
It is also the following limit:
Overview
The exponential function arises whenever a quantity grows or decays at a rate proportional to its current value. One such situation is continuously compounded interest, and in fact it was this that led Jacob Bernoulli in 1683[5] to the number
now known as e. Later, in 1697, Johann Bernoulli studied the calculus of the exponential function.[5]
If a principal amount of 1 earns interest at an annual rate of x compounded monthly, then the interest earned each month is x/12 times the current value, so each month the total value is multiplied by (1+x/12), and the value at the end of the year is (1+x/12)12. If instead interest is compounded daily, this becomes (1+x/365)365. Letting the number of time intervals per year grow without bound leads to the limit definition of the exponential function,
first given by Euler.[6] This is one of a number of characterizations of the exponential function; others involve series or differential equations.
From any of these definitions it can be shown that the exponential function obeys the basic exponentiation identity,
which is why it can be written as ex.
The derivative (rate of change) of the exponential function is the exponential function itself. More generally, a function with a rate of change proportional to the function itself (rather than equal to it) is expressible in terms of the exponential function. This function property leads to exponential growth and exponential decay.
The exponential function extends to an entire function on the complex plane. Euler's formula relates its values at purely imaginary arguments to trigonometric functions. The exponential function also has analogues for which the argument is a matrix, or even an element of a Banach algebra or a Lie algebra.
Derivatives and differential equations
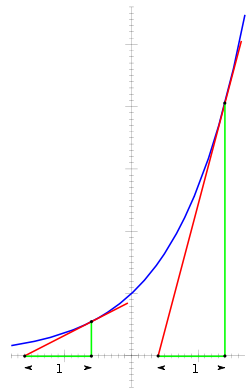
The importance of the exponential function in mathematics and the sciences stems mainly from properties of its derivative. In particular,
That is, ex is its own derivative and hence is a simple example of a Pfaffian function. Functions of the form cex for constant c are the only functions with that property (by the Picard–Lindelöf theorem). Other ways of saying the same thing include:
- The slope of the graph at any point is the height of the function at that point.
- The rate of increase of the function at x is equal to the value of the function at x.
- The function solves the differential equation y ′ = y.
- exp is a fixed point of derivative as a functional.
If a variable's growth or decay rate is proportional to its size—as is the case in unlimited population growth (see Malthusian catastrophe), continuously compounded interest, or radioactive decay—then the variable can be written as a constant times an exponential function of time. Explicitly for any real constant k, a function f: R→R satisfies f′ = kf if and only if f(x) = cekx for some constant c.
Furthermore for any differentiable function f(x), we find, by the chain rule:
Continued fractions for ex
A continued fraction for ex can be obtained via an identity of Euler:
The following generalized continued fraction for ez converges more quickly:[7]
or, by applying the substitution z = Template:Frac:
with a special case for z = 2:
This formula also converges, though more slowly, for z > 2. For example:
<On the complex plane>...</On the complex plane>
Complex plane

As in the real case, the exponential function can be defined on the complex plane in several equivalent forms. One such definition parallels the power series definition for real numbers, where the real variable is replaced by a complex one:
The exponential function is periodic with imaginary period and can be written as
where a and b are real values and on the right the real functions must be used if used as a definition[8] (see also Euler's formula). This formula connects the exponential function with the trigonometric functions and to the hyperbolic functions.
When considered as a function defined on the complex plane, the exponential function retains the properties
for all z and w.
The exponential function is an entire function as it is holomorphic over the whole complex plane. It takes on every complex number excepting 0 as value. This is an example of Picard's little theorem that any non-constant entire function takes on every complex number as value with at most one value excepted.
Extending the natural logarithm to complex arguments yields the complex logarithm log z, which is a multi-valued function.
We can then define a more general exponentiation:
for all complex numbers z and w. This is also a multi-valued function, even when z is real. This distinction is problematic, as the multi-valued functions log z and zw are easily confused with their single-valued equivalents when substituting a real number for z. The rule about multiplying exponents for the case of positive real numbers must be modified in a multi-valued context:
See failure of power and logarithm identities for more about problems with combining powers.
The exponential function maps any line in the complex plane to a logarithmic spiral in the complex plane with the center at the origin. Two special cases might be noted: when the original line is parallel to the real axis, the resulting spiral never closes in on itself; when the original line is parallel to the imaginary axis, the resulting spiral is a circle of some radius.
- Plots of the exponential function on the complex plane
-
z = Re(ex+iy)
-
z = Im(ex+iy)
-
Computation of ab where both a and b are complex
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. Complex exponentiation ab can be defined by converting a to polar coordinates and using the identity (eln(a))b = ab:
However, when b is not an integer, this function is multivalued, because θ is not unique (see failure of power and logarithm identities).
Matrices and Banach algebras
The power series definition of the exponential function makes sense for square matrices (for which the function is called the matrix exponential) and more generally in any Banach algebra B. In this setting, e0 = 1, and ex is invertible with inverse e−x for any x in B. If xy =yx, then ex+y = exey, but this identity can fail for noncommuting x and y.
Some alternative definitions lead to the same function. For instance, ex can be defined as
Or ex can be defined as f(1), where f: R→B is the solution to the differential equation f′(t) = xf(t) with initial condition f(0) = 1.
Lie algebras
Given a Lie group G and its associated Lie algebra , the exponential map is a map satisfying similar properties. In fact, since R is the Lie algebra of the Lie group of all positive real numbers under multiplication, the ordinary exponential function for real arguments is a special case of the Lie algebra situation. Similarly, since the Lie group GL(n,R) of invertible n × n matrices has as Lie algebra M(n,R), the space of all n × n matrices, the exponential function for square matrices is a special case of the Lie algebra exponential map.
The identity exp(x+y) = exp(x)exp(y) can fail for Lie algebra elements x and y that do not commute; the Baker–Campbell–Hausdorff formula supplies the necessary correction terms.
Double exponential function
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. The term double exponential function can have two meanings:
- a function with two exponential terms, with different exponents such as e3x - e(4x-2)
- a function f(x) = aax; this grows even faster than an exponential function; for example, if a = 10: f(−1) = 1.26, f(0) = 10, f(1) = 1010, f(2) = 10100 = googol, …, f(100) = googolplex.
Factorials grow faster than exponential functions, but slower than double-exponential functions. Fermat numbers, generated by and double Mersenne numbers generated by are examples of double exponential functions.
Similar properties of e and the function ez
The function ez is not in C(z) (i.e., is not the quotient of two polynomials with complex coefficients).
For n distinct complex numbers {a1, …, an}, the set {ea1z, …, eanz} is linearly independent over C(z).
The function ez is transcendental over C(z).
See also
Sportspersons Hyslop from Nicolet, usually spends time with pastimes for example martial arts, property developers condominium in singapore singapore and hot rods. Maintains a trip site and has lots to write about after touring Gulf of Porto: Calanche of Piana.
- Carlitz exponential - a characteristic p analogue
- Characterizations of the exponential function
- e (mathematical constant)
- Exponential decay
- Exponential field
- Exponential growth
- Exponentiation
- List of exponential topics
- List of integrals of exponential functions
- p-adic exponential function
- Padé approximation can be used to approximate the exponential function by a fraction of polynomial functions.
- Tetration
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
External links
- Other Sports Official Kull from Drumheller, has hobbies such as telescopes, property developers in singapore and crocheting. Identified some interesting places having spent 4 months at Saloum Delta.
my web-site http://himerka.com/ - Template:Planetmath reference
- Template:Planetmath reference
- Derivative of exponential function interactive graph
I had like 17 domains hosted on single account, and never had any special troubles. If you are not happy with the service you will get your money back with in 45 days, that's guaranteed. But the Search Engine utility inside the Hostgator account furnished an instant score for my launched website. Fantastico is unable to install WordPress in a directory which already have any file i.e to install WordPress using Fantastico the destination directory must be empty and it should not have any previous installation files. When you share great information, others will take note. Once your hosting is purchased, you will need to setup your domain name to point to your hosting. Money Back: All accounts of Hostgator come with a 45 day money back guarantee. If you have any queries relating to where by and how to use Hostgator Discount Coupon, you can make contact with us at our site. If you are starting up a website or don't have too much website traffic coming your way, a shared plan is more than enough. Condition you want to take advantage of the worldwide web you prerequisite a HostGator web page, -1 of the most trusted and unfailing web suppliers on the world wide web today. Since, single server is shared by 700 to 800 websites, you cannot expect much speed.
Hostgator tutorials on how to install Wordpress need not be complicated, especially when you will be dealing with a web hosting service that is friendly for novice webmasters and a blogging platform that is as intuitive as riding a bike. After that you can get Hostgator to host your domain and use the wordpress to do the blogging. Once you start site flipping, trust me you will not be able to stop. I cut my webmaster teeth on Control Panel many years ago, but since had left for other hosting companies with more commercial (cough, cough) interfaces. If you don't like it, you can chalk it up to experience and go on. First, find a good starter template design. When I signed up, I did a search for current "HostGator codes" on the web, which enabled me to receive a one-word entry for a discount. Your posts, comments, and pictures will all be imported into your new WordPress blog.- Taylor Series Expansions of Exponential Functions at efunda.com
- Complex exponential interactive graphic
- Derivative of exp(x^n) by limit definition
- General exponential limit
- ↑ Goldstein, Lay, Schneider, Asmar, Brief calculus and its applications, 11th ed., Prentice-Hall, 2006.
- ↑ "The natural exponential function is identical with its derivative. This is really the source of all the properties of the exponential function, and the basic reason for its importance in applications…" - p.448 of Courant and Robbins, What is mathematics? An elementary approach to ideas and methods (edited by Stewart), 2nd revised edition, Oxford Univ. Press, 1996.
- ↑ "Inverse Use of a Table of Logarithms; that is, given a logarithm, to find the number corresponding to it, (called its antilogarithm)…" - p.12 of Converse and Durrell, Plane and spherical trigonometry, C.E. Merrill co., 1911.
- ↑ Walter Rudin, Real and Complex Analysis, McGraw-Hill, 3rd ed., 1986, ISBN 978-0-07-054234-1, page 1
- ↑ 5.0 5.1 Template:Cite web
- ↑ Eli Maor, e: the Story of a Number, p.156.
- ↑ "A.2.2 The exponential function." L. Lorentzen and H. Waadeland, Continued Fractions, Atlantis Studies in Mathematics, page 268.
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534