Uses of trigonometry: Difference between revisions
en>Pharaoh of the Wizards m Reverted edits by 117.193.244.255 (talk) to last revision by Fraggle81 (HG) |
en>Donner60 Reverted 2 edits by 92.98.43.109 (talk) to last revision by 122.172.6.125. (TW) |
||
| Line 1: | Line 1: | ||
[[File:Fano plane Hasse diagram.svg|thumb|[[Hasse diagram]] of a complemented lattice<br>A point and a line of the [[Fano plane]] are complements, when <math>~p \notin l~</math>]] | |||
In the [[mathematics|mathematical]] discipline of [[order theory]], a '''complemented lattice''' is a bounded [[lattice (order)|lattice]] (with [[least element]] 0 and [[greatest element]] 1), in which every element ''a'' has a '''complement''', i.e. an element ''b'' satisfying ''a'' ∨ ''b'' = 1 and ''a'' ∧ ''b'' = 0. | |||
A '''relatively complemented lattice''' is a lattice such that every [[Partially_ordered_set#Interval|interval]] [''c'', ''d''] is complemented. Complements need not be unique. | |||
An '''orthocomplementation''' on a complemented lattice is an [[involution (mathematics)|involution]] which is [[order-reversing]] and maps each element to a complement. An orthocomplemented lattice satisfying a weak form of the [[modular lattice|modular law]] is called an '''orthomodular lattice'''. | |||
In [[distributive lattice]]s, complements are unique. Every complemented distributive lattice has a unique orthocomplementation and is in fact a [[Boolean algebra (structure)|Boolean algebra]]. | |||
==Definition and basic properties== | |||
A '''complemented lattice''' is a bounded lattice (with [[least element]] 0 and [[greatest element]] 1), in which every element ''a'' has a '''complement''', i.e. an element ''b'' such that | |||
::''a'' ∨ ''b'' = 1 and ''a'' ∧ ''b'' = 0. | |||
In general an element may have more than one complement. However, in a bounded [[distributive lattice]] every element will have at most one complement.<ref>Grätzer (1971), Lemma I.6.1, p. 47. Rutherford (1965), Theorem 9.3 p. 25.</ref> A lattice in which every element has exactly one complement is called a '''uniquely complemented lattice'''. | |||
A lattice with the property that every interval is complemented is called a '''relatively complemented lattice'''. In other words, a relatively complemented lattice is characterized by the property that for every element ''a'' in an interval [''c'', ''d''] there is an element ''b'' such that | |||
::''a'' ∨ ''b'' = ''d'' and ''a'' ∧ ''b'' = ''c''. | |||
Such an element ''b'' is called a complement of ''a'' relative to the interval. A distributive lattice is complemented if and only if it is bounded and relatively complemented.<ref>Grätzer (1971), Lemma I.6.2, p. 48. This result holds more generally for modular lattices, see Exercise 4, p. 50.</ref><ref>Birkhoff (1961), Corollary IX.1, p. 134</ref> | |||
==Orthocomplementation== | |||
An '''orthocomplementation''' on a bounded lattice is a function that maps each element ''a'' to an "orthocomplement" ''a''<sup>⊥</sup> in such a way that the following axioms are satisfied: | |||
;Complement law: ''a''<sup>⊥</sup> ∨ ''a'' = 1 and ''a''<sup>⊥</sup> ∧ ''a'' = 0. | |||
;Involution law: ''a''<sup>⊥⊥</sup> = ''a''. | |||
;Order-reversing: if ''a'' ≤ ''b'' then ''b''<sup>⊥</sup> ≤ ''a''<sup>⊥</sup>. | |||
An '''orthocomplemented lattice''' or '''ortholattice''' is a bounded lattice which is equipped with an orthocomplementation. The lattices of subspaces of [[inner product space]]s, and the [[orthogonal complement]] operation in these lattices, provide examples of orthocomplemented lattices that are not, in general, distributive.<ref>[http://unapologetic.wordpress.com/2009/05/07/orthogonal-complements-and-the-lattice-of-subspaces/ The Unapologetic Mathematician: Orthogonal Complements and the Lattice of Subspaces].</ref> | |||
<gallery Caption="Some complemented lattices"> | |||
Image:Smallest_nonmodular_lattice_1.svg|In the pentagon lattice ''N''<sub>5</sub>, the node on the right-hand side has two complements. | |||
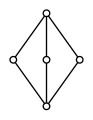
Image:Diamond lattice.svg|The diamond lattice ''M''<sub>3</sub> admits no orthocomplementation. | |||
Image:Lattice M4.svg|The lattice ''M''<sub>4</sub> admits 3 orthocomplementations. | |||
Image:Hexagon lattice.svg|The hexagon lattice admits a unique orthocomplementation, but it is not uniquely complemented. | |||
</gallery> | |||
[[Boolean algebra (structure)|Boolean algebras]] are a special case of orthocomplemented lattices, which in turn are a special case of complemented lattices (with extra structure). These structures are most often used in [[quantum logic]], where the [[Closed set|closed]] [[Linear subspace|subspaces]] of a [[Separable space|separable]] [[Hilbert space]] represent quantum propositions and behave as an orthocomplemented lattice. | |||
Orthocomplemented lattices, like Boolean algebras, satisfy [[de Morgan's laws]]: | |||
* (''a'' ∨ ''b'')<sup>⊥</sup> = ''a''<sup>⊥</sup> ∧ ''b''<sup>⊥</sup> | |||
* (''a'' ∧ ''b'')<sup>⊥</sup> = ''a''<sup>⊥</sup> ∨ ''b''<sup>⊥</sup>. | |||
==Orthomodular lattices== | |||
A lattice is called [[modular lattice|modular]] if for all elements ''a'', ''b'' and ''c'' the implication | |||
::if ''a'' ≤ ''c'', then ''a'' ∨ (''b'' ∧ ''c'') = (''a'' ∨ ''b'') ∧ ''c'' | |||
holds. This is weaker than distributivity; e.g. the above-shown lattice ''M''<sub>3</sub> is modular, but not distributive. A natural further weakening of this condition for orthocomplemented lattices, necessary for applications in quantum logic, is to require it only in the special case ''b'' = ''a''<sup>⊥</sup>. An '''orthomodular lattice''' is therefore defined as an orthocomplemented lattice such that for any two elements the implication | |||
::if ''a'' ≤ ''c'', then ''a'' ∨ (''a''<sup>⊥</sup> ∧ ''c'') = ''c'' | |||
holds. | |||
Lattices of this form are of crucial importance for the study of [[quantum logic]], since they are part of the axiomisation of the [[Hilbert space]] [[mathematical formulation of quantum mechanics|formulation]] of [[quantum mechanics]]. [[Garrett Birkhoff]] and [[John von Neumann]] observed that the propositional calculus in quantum logic is "formally indistinguishable from the calculus of linear subspaces [of a Hilbert space] with respect to set products, linear sums and orthogonal complements" corresponding to the roles of ''and'', ''or'' and ''not'' in Boolean lattices. This remark has spurred interest in the closed subspaces of a Hilbert space, which form an orthomodular lattice.<ref name="PadmanabhanRudeanu2008">{{cite book|author1=Ranganathan Padmanabhan|author2=Sergiu Rudeanu|title=Axioms for lattices and boolean algebras|url=http://books.google.com/books?id=JlXSlpmlSv4C&pg=PA128|year=2008|publisher=World Scientific|isbn=978-981-283-454-6|page=128}}</ref> | |||
==External links== | |||
{| style="float:right" | |||
| {{Algebraic structures |Lattice}} | |||
|} | |||
* {{planetmath reference|id=6754|title=Complemented lattice}} | |||
* {{planetmath reference|id=7852|title=Relative complement}} | |||
* {{planetmath reference|id=10477|title=Uniquely complemented lattice}} | |||
* {{planetmath reference|id=7822|title=Orthocomplemented lattice}} | |||
==Notes== | |||
{{Reflist}} | |||
==References== | |||
* {{Cite book | last1=Birkhoff | first1=Garrett | title=Lattice Theory | publisher=American Mathematical Society | year=1961 }} | |||
* {{Cite book | last1=Grätzer | first1=George | title=Lattice Theory: First Concepts and Distributive Lattices | publisher=W. H. Freeman and Company | isbn=978-0-7167-0442-3 | year=1971 }} | |||
* {{Cite book | last1=Grätzer | first1=George | title=General Lattice Theory | publisher=Birkhäuser | location=Basel, Switzerland | isbn=978-0-12-295750-5 | year=1978 | postscript=<!--None-->}} | |||
* {{cite book | first = Daniel Edwin | last = Rutherford | year = 1965 | title = Introduction to Lattice Theory | publisher = Oliver and Boyd }} | |||
[[Category:Lattice theory]] | |||
Revision as of 07:22, 6 November 2013

A point and a line of the Fano plane are complements, when
In the mathematical discipline of order theory, a complemented lattice is a bounded lattice (with least element 0 and greatest element 1), in which every element a has a complement, i.e. an element b satisfying a ∨ b = 1 and a ∧ b = 0. A relatively complemented lattice is a lattice such that every interval [c, d] is complemented. Complements need not be unique.
An orthocomplementation on a complemented lattice is an involution which is order-reversing and maps each element to a complement. An orthocomplemented lattice satisfying a weak form of the modular law is called an orthomodular lattice.
In distributive lattices, complements are unique. Every complemented distributive lattice has a unique orthocomplementation and is in fact a Boolean algebra.
Definition and basic properties
A complemented lattice is a bounded lattice (with least element 0 and greatest element 1), in which every element a has a complement, i.e. an element b such that
- a ∨ b = 1 and a ∧ b = 0.
In general an element may have more than one complement. However, in a bounded distributive lattice every element will have at most one complement.[1] A lattice in which every element has exactly one complement is called a uniquely complemented lattice.
A lattice with the property that every interval is complemented is called a relatively complemented lattice. In other words, a relatively complemented lattice is characterized by the property that for every element a in an interval [c, d] there is an element b such that
- a ∨ b = d and a ∧ b = c.
Such an element b is called a complement of a relative to the interval. A distributive lattice is complemented if and only if it is bounded and relatively complemented.[2][3]
Orthocomplementation
An orthocomplementation on a bounded lattice is a function that maps each element a to an "orthocomplement" a⊥ in such a way that the following axioms are satisfied:
- Complement law
- a⊥ ∨ a = 1 and a⊥ ∧ a = 0.
- Involution law
- a⊥⊥ = a.
- Order-reversing
- if a ≤ b then b⊥ ≤ a⊥.
An orthocomplemented lattice or ortholattice is a bounded lattice which is equipped with an orthocomplementation. The lattices of subspaces of inner product spaces, and the orthogonal complement operation in these lattices, provide examples of orthocomplemented lattices that are not, in general, distributive.[4]
- Some complemented lattices
-
In the pentagon lattice N5, the node on the right-hand side has two complements.
-
The diamond lattice M3 admits no orthocomplementation.
-
The lattice M4 admits 3 orthocomplementations.
-
The hexagon lattice admits a unique orthocomplementation, but it is not uniquely complemented.
Boolean algebras are a special case of orthocomplemented lattices, which in turn are a special case of complemented lattices (with extra structure). These structures are most often used in quantum logic, where the closed subspaces of a separable Hilbert space represent quantum propositions and behave as an orthocomplemented lattice.
Orthocomplemented lattices, like Boolean algebras, satisfy de Morgan's laws:
- (a ∨ b)⊥ = a⊥ ∧ b⊥
- (a ∧ b)⊥ = a⊥ ∨ b⊥.
Orthomodular lattices
A lattice is called modular if for all elements a, b and c the implication
- if a ≤ c, then a ∨ (b ∧ c) = (a ∨ b) ∧ c
holds. This is weaker than distributivity; e.g. the above-shown lattice M3 is modular, but not distributive. A natural further weakening of this condition for orthocomplemented lattices, necessary for applications in quantum logic, is to require it only in the special case b = a⊥. An orthomodular lattice is therefore defined as an orthocomplemented lattice such that for any two elements the implication
- if a ≤ c, then a ∨ (a⊥ ∧ c) = c
holds.
Lattices of this form are of crucial importance for the study of quantum logic, since they are part of the axiomisation of the Hilbert space formulation of quantum mechanics. Garrett Birkhoff and John von Neumann observed that the propositional calculus in quantum logic is "formally indistinguishable from the calculus of linear subspaces [of a Hilbert space] with respect to set products, linear sums and orthogonal complements" corresponding to the roles of and, or and not in Boolean lattices. This remark has spurred interest in the closed subspaces of a Hilbert space, which form an orthomodular lattice.[5]
External links
| Template:Algebraic structures |
- Template:Planetmath reference
- Template:Planetmath reference
- Template:Planetmath reference
- Template:Planetmath reference
Notes
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
References
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
- ↑ Grätzer (1971), Lemma I.6.1, p. 47. Rutherford (1965), Theorem 9.3 p. 25.
- ↑ Grätzer (1971), Lemma I.6.2, p. 48. This result holds more generally for modular lattices, see Exercise 4, p. 50.
- ↑ Birkhoff (1961), Corollary IX.1, p. 134
- ↑ The Unapologetic Mathematician: Orthogonal Complements and the Lattice of Subspaces.
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534