Cotorsion group

A function (in black) is convex if and only if the region above its graph (in green) is a convex set. This region is the function's epigraph.

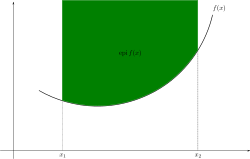
In mathematics, the epigraph of a function f : Rⁿ→R is the set of points lying on or above its graph:

$\text{epi}f=\{(x,\mu ):x\in {\mathbb{ℝ}}^n,\mu \in \mathbb{ℝ},\mu \ge f(x)\}\subseteq {\mathbb{ℝ}}^{n+1}.$

The strict epigraph is the epigraph with the graph itself removed:

${\text{epi}}_{S}f=\{(x,\mu ):x\in {\mathbb{ℝ}}^n,\mu \in \mathbb{ℝ},\mu >f(x)\}\subseteq {\mathbb{ℝ}}^{n+1}.$

The same definitions are valid for a function that takes values in R ∪ ∞. In this case, the epigraph is empty if and only if f is identically equal to infinity.

Similarly, the set of points on or below the function is its hypograph.

Properties

A function is convex if and only if its epigraph is a convex set. The epigraph of a real affine function g : Rⁿ→R is a halfspace in Rⁿ⁺¹.

A function is lower semicontinuous if and only if its epigraph is closed.

References

• Rockafellar, Ralph Tyrell (1996), Convex Analysis, Princeton University Press, Princeton, NJ. ISBN 0-691-01586-4.