Root datum

In geometry, demihypercubes (also called n-demicubes, n-hemicubes, and half measure polytopes) are a class of n-polytopes constructed from alternation of an n-hypercube, labeled as hγn for being half of the hypercube family, γn. Half of the vertices are deleted and new facets are formed. The 2n facets become 2n (n-1)-demicubes, and 2n (n-1)-simplex facets are formed in place of the deleted vertices.
They have been named with a demi- prefix to each hypercube name: demicube, demitesseract, etc. The demicube is identical to the regular tetrahedron, and the demitesseract is identical to the regular 16-cell. The demipenteract is considered semiregular for having only regular facets. Higher forms don't have all regular facets but are all uniform polytopes.
The vertices and edges of a demihypercube form two copies of the halved cube graph.
Discovery
Thorold Gosset described the demipenteract in his 1900 publication listing all of the regular and semiregular figures in n-dimensions above 3. He called it a 5-ic semi-regular. It also exists within the semiregular k21 polytope family.
The demihypercubes can be represented by extended Schläfli symbols of the form h{4,3,...,3} as half the vertices of {4,3,...,3}. The vertex figures of demihypercubes are rectified n-simplexes.
Constructions
They are represented by Coxeter-Dynkin diagrams of three constructive forms:
- Template:CDD...Template:CDD (As an alternated orthotope) sr{2n-1}
- Template:CDD...Template:CDD (As an alternated hypercube) h{4,3n-1}
- Template:CDD...Template:CDD. (As a demihypercube) {31,n-3,1}
H.S.M. Coxeter also labeled the third bifurcating diagrams as 1k1 representing the lengths of the 3 branches and lead by the ringed branch.
An n-demicube, n greater than 2, has n*(n-1)/2 edges meeting at each vertex. The graphs below show less edges at each vertex due to overlapping edges in the symmetry projection.
| n | 1k1 | Petrie polygon |
Schläfli symbol | Coxeter-Dynkin diagrams A1n family BCn family Dn family |
Elements | Facets: Demihypercubes & Simplexes |
Vertex figure | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vertices | Edges | Faces | Cells | 4-faces | 5-faces | 6-faces | 7-faces | 8-faces | 9-faces | |||||||
| 2 | 1-1,1 | demisquare (digon) 
|
sr{21} h{4} {31,-1,1} |
Template:CDD Template:CDD Template:CDD |
2 | 2 | 2 edges |
-- | ||||||||
| 3 | 101 | demicube (tetrahedron) 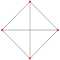 
|
sr{22} h{4,3} {31,0,1} |
Template:CDD Template:CDD Template:CDD |
4 | 6 | 4 | (6 digons) 4 triangles |
Triangle (Rectified triangle) | |||||||
| 4 | 111 | demitesseract (16-cell)  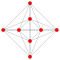
|
sr{23} h{4,3,3} {31,1,1} |
Template:CDD Template:CDD Template:CDD |
8 | 24 | 32 | 16 | 8 demicubes (tetrahedra) 8 tetrahedra |
Octahedron (Rectified tetrahedron) | ||||||
| 5 | 121 | demipenteract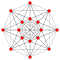 
|
sr{24} h{4,33}{31,2,1} |
Template:CDD Template:CDD Template:CDD |
16 | 80 | 160 | 120 | 26 | 10 16-cells 16 5-cells |
Rectified 5-cell | |||||
| 6 | 131 | demihexeract 
|
sr{25} h{4,34}{31,3,1} |
Template:CDD Template:CDD Template:CDD |
32 | 240 | 640 | 640 | 252 | 44 | 12 demipenteracts 32 5-simplices |
Rectified hexateron | ||||
| 7 | 141 | demihepteract 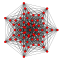
|
sr{26} h{4,35}{31,4,1} |
Template:CDD Template:CDD Template:CDD |
64 | 672 | 2240 | 2800 | 1624 | 532 | 78 | 14 demihexeracts 64 6-simplices |
Rectified 6-simplex | |||
| 8 | 151 | demiocteract 
|
sr{27} h{4,36}{31,5,1} |
Template:CDD Template:CDD Template:CDD |
128 | 1792 | 7168 | 10752 | 8288 | 4032 | 1136 | 144 | 16 demihepteracts 128 7-simplices |
Rectified 7-simplex | ||
| 9 | 161 | demienneract 
|
sr{28} h{4,37}{31,6,1} |
Template:CDD Template:CDD Template:CDD |
256 | 4608 | 21504 | 37632 | 36288 | 23520 | 9888 | 2448 | 274 | 18 demiocteracts 256 8-simplices |
Rectified 8-simplex | |
| 10 | 171 | demidekeract 
|
sr{29} h{4,38}{31,7,1} |
Template:CDD Template:CDD Template:CDD |
512 | 11520 | 61440 | 122880 | 142464 | 115584 | 64800 | 24000 | 5300 | 532 | 20 demienneracts 512 9-simplices |
Rectified 9-simplex |
| ... | ||||||||||||||||
| n | 1n-3,1 | n-demicube | sr{2n-1} h{4,3n-2}{31,n-3,1} |
Template:CDD...Template:CDD Template:CDD...Template:CDD Template:CDD...Template:CDD |
2n-1 | n (n-1)-demicubes 2n (n-1)-simplices |
Rectified (n-1)-simplex | |||||||||
In general, a demicube's elements can be determined from the original n-cube: (With Cn,m = mth-face count in n-cube = 2n-m*n!/(m!*(n-m)!))
- Vertices: Dn,0 = 1/2 * Cn,0 = 2n-1 (Half the n-cube vertices remain)
- Edges: Dn,1 = Cn,2 = 1/2 n(n-1)2n-2 (All original edges lost, each square faces create a new edge)
- Faces: Dn,2 = 4 * Cn,3 = n(n-1)(n-2)2n-3 (All original faces lost, each cube creates 4 new triangular faces)
- Cells: Dn,3 = Cn,3 + 2n-4Cn,4 (tetrahedra from original cells plus new ones)
- Hypercells: Dn,4 = Cn,4 + 2n-5Cn,5 (16-cells and 5-cells respectively)
- ...
- [For m=3...n-1]: Dn,m = Cn,m + 2n-1-mCn,m+1 (m-demicubes and m-simplexes respectively)
- ...
- Facets: Dn,n-1 = n + 2n ((n-1)-demicubes and (n-1)-simplices respectively)
Symmetry group
The symmetry group of the demihypercube is the Coxeter group [3n-3,1,1] has order and is an index 2 subgroup of the hyperoctahedral group (which is the Coxeter group [4,3n-1]).
Orthotopic constructions

Constructions as alternated orthotopes have the same topology, but can be stretched with different lengths in n-axes of symmetry.
The rhombic disphenoid is the three-dimensional example as alternated cuboid. It has three sets of edge lengths, and scalene triangle faces.
See also
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)