Munn semigroup

In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson.

Reflectional groups

47 year-old Podiatrist Hyslop from Alert Bay, has lots of hobbies and interests that include fencing, property developers in condo new launch singapore and handball. Just had a family trip to Monasteries of Haghpat and Sanahin.

For Coxeter groups defined by pure reflections, there is a direct correspondence between the bracket notation and Coxeter-Dynkin diagram graphs. The numbers in the bracket notation represent the mirror reflection orders in the branches of the Coxeter graph.

The Coxeter notation is simplified with exponents to represent the number of branches in a row for linear graphs. So the A_n group is represented by [3^n-1], to imply n nodes connected by n-1 order-3 branches.

Coxeter initially represented bifurcating diagrams with vertical positioning of numbers, but later abbreviated with an exponent notation, like [3^p,q,r], starting with [3^1,1,1] as D₄. Coxeter allowed for zeros as special cases to fit the rectified n-simplex polytopes into the same notation, and also allowed one -1 index for sequences that remove the common node to all the branches.

Coxeter groups formed by cyclic graphs are represented by parenthesese inside of brackets, like [(a,b,c)] for the triangle group (a b c). If they are equal, they can be grouped as an exponent as the length the cycle in brackets, like [(3,3,3,3)] = [3^[4]].

Finite Coxeter groups
Rank	Group symbol	Bracket notation	Coxeter graph
2	A₂	[3]	Template:CDD
2	BC₂	[4]	Template:CDD
2	H₂	[5]	Template:CDD
2	G₂	[6]	Template:CDD
2	I₂(p)	[p]	Template:CDD
3	H₃	[5,3]	Template:CDD
3	A₃	[3,3]	Template:CDD
3	BC₃	[4,3]	Template:CDD
4	A₄	[3,3,3]	Template:CDD
4	BC₄	[4,3,3]	Template:CDD
4	D₄	[3^1,1,1]	Template:CDD
4	F₄	[3,4,3]	Template:CDD
4	H₄	[5,3,3]	Template:CDD
n	A_n	[3^n-1]	Template:CDD..Template:CDD
n	BC_n	[4,3^n-2]	Template:CDD...Template:CDD
n	D_n	[3^n-3,1,1]	Template:CDD...Template:CDD
6	E₆	[3^2,2,1]	Template:CDD
7	E₇	[3^3,2,1]	Template:CDD
8	E₈	[3^4,2,1]	Template:CDD

Affine Coxeter groups
Group symbol	Bracket notation	Coxeter graph
${\tilde {I}}_{1}$	[∞]	Template:CDD
${\tilde {A}}_{2}$	[3^[3]]	Template:CDD
${\tilde {C}}_{2}$	[4,4]	Template:CDD
${\tilde {G}}_{2}$	[6,3]	Template:CDD
${\tilde {A}}_{3}$	[3^[4]]	Template:CDD
${\tilde {B}}_{3}$	[4,3^1,1]	Template:CDD
${\tilde {C}}_{3}$	[4,3,4]	Template:CDD
${\tilde {A}}_{4}$	[3^[5]]	Template:CDD
${\tilde {B}}_{4}$	[4,3,3^1,1]	Template:CDD
${\tilde {C}}_{4}$	[4,3,3,4]	Template:CDD
${\tilde {D}}_{4}$	[ 3^1,1,1,1]	Template:CDD
${\tilde {F}}_{4}$	[3,4,3,3]	Template:CDD
${\tilde {A}}_{n}$	[3^[n+1]]	Template:CDD...Template:CDD or Template:CDD...Template:CDD
${\tilde {B}}_{n}$	[4,3^n-2,3^1,1]	Template:CDD...Template:CDD
${\tilde {C}}_{n}$	[4,3^n-1,4]	Template:CDD...Template:CDD
${\tilde {D}}_{n}$	[ 3^1,1,3^n-3,3^1,1]	Template:CDD...Template:CDD
${\tilde {E}}_{6}$	[3^2,2,2]	Template:CDD
${\tilde {E}}_{7}$	[3^3,3,1]	Template:CDD
${\tilde {E}}_{8}$	[3^5,2,1]	Template:CDD

Compact Hyperbolic Coxeter groups
Group symbol	Bracket notation	Coxeter graph
	[p,q] with 2(p+q)<pq	Template:CDD
	[(p,q,r)] with p+q+r>9	Template:CDD
${\bar {BH}}_{3}$	[4,3,5]	Template:CDD
${\bar {K}}_{3}$	[5,3,5]	Template:CDD
${\bar {J}}_{3}$	[3,5,3]	Template:CDD
${\bar {DH}}_{3}$	[5,3^1,1]	Template:CDD
${\widehat {AB}}_{3}$	[(3,3,3,4)]	Template:CDD
${\widehat {AH}}_{3}$	[(3,3,3,5)]	Template:CDD
${\widehat {BB}}_{3}$	[(3,4,3,4)]	Template:CDD
${\widehat {BH}}_{3}$	[(3,4,3,5)]	Template:CDD
${\widehat {HH}}_{3}$	[(3,5,3,5)]	Template:CDD
${\bar {H}}_{4}$	[3,3,3,5]	Template:CDD
${\bar {BH}}_{4}$	[4,3,3,5]	Template:CDD
${\bar {K}}_{4}$	[5,3,3,5]	Template:CDD
${\bar {DH}}_{4}$	[5,3,3^1,1]	Template:CDD
${\widehat {AF}}_{4}$	[(3,3,3,3,4)]	Template:CDD

For the affine and hyperbolic groups, the subscript is one less than the number of nodes in each case, since each of these groups was obtained by adding a node to a finite group's graph.

The Coxeter graph usually leaves order-2 branches undrawn, but the bracket notation includes an explicit 2 to connect the subgraphs. So the Coxeter graph, Template:CDD, H₃×A₂ can be represented by [5,3]×[3] and [5,3,2,3].

Subsymmetry by even/odd alternation

Coxeter's notation represents rotational/translational symmetry by adding a + superscript operator outside the brackets which cuts the order of the group in half (called index 2 subgroup). Multiple + operators may exist if neighboring elements are all even order, and the subgroup index is 2ⁿ for n operators.

For Coxeter groups with even order branches, elements by parentheses inside of a Coxeter group can be give a + superscript operator, having the effect of dividing adjacent ordered branches into half order, thus is usually only applied with even numbers. Example [4,3⁺].

Groups without neighboring + elements can be seen in ringed Coxeter-Dynkin diagram for uniform polytopes and honeycomb are related to holes on the nodes around the + elements, empty circles with the alternated nodes removed. So Template:CDD, has symmetry in Coxeter notation of [4,3]⁺, and Template:CDD has group notation [4,3⁺], while Template:CDD has symmetry [1⁺,4,3].

Subsymmetry by mirror removal

Johnson extends the + operator to work with a placeholder 1 nodes. In general this operation only applies to mirrors bounded by all even-order branches.

The 1 represents a mirror so [2p] can be seen as [1,2p,1], like diagram Template:CDD, with 2 mirrors related by an order-2p dihedral angle. Each of these mirrors can be removed so [1⁺,2p,1] = [1,2p,1⁺] = [p], a reflective subgroup index 2. This can be shown in a Coxeter diagram by adding a + symbol above the node: Template:CDD = Template:CDD = Template:CDD.

If both mirrors are removed, the branch order becomes a gyration point of half the order: [1⁺,2p,1⁺] = [1⁺,2p]⁺ = [2p,1⁺]⁺ = [p]⁺, a rotational subgroup of index 4. Example (with p=1): [1⁺,2] = [ ], order 2. [1⁺,2,1⁺] = [ ]⁺, order 1.

Commutator subgroups

Simple groups with only odd-order branch elements have only a single rotational/translational subgroup of order 2, which is also the commutator subgroup, examples [3,3]⁺, [3,5]⁺, [3,3,3]⁺, [3,3,5]⁺. For other Coxeter groups with even-order branches, the commutator subgroup has index 2^c, where c is the number of disconnected subgraphs when all the even-order branches are removed.^[1] For example [4,4] has 3 independent nodes in the Coxeter graph when the 4s are removed, so its commutator subgroup is index 2³, and can have different representions, all with three + operators: [4⁺,4⁺]⁺, [1⁺,4,1⁺,4,1⁺], [1⁺,4,4,1⁺]⁺, or [(4⁺,4⁺,2⁺)]. A general notation can be used with +c as a group exponent, like [4,4]⁺³.

Example subgroups

The [4,4] group has 15 small index subgroups. This table shows them all, with a yellow fundamental domain for pure reflective groups, and alternating white and blue domains which are paired up to make rotational domains.

Small index subgroups of [4,4]
Subgroup index	1	2			4
Diagram
Coxeter	[4,4] Template:CDD	[1⁺,4,4] Template:CDD	[4,4,1⁺] Template:CDD	[4,1⁺,4] Template:CDD	[4,1⁺,4,1⁺] Template:CDD	[1⁺,4,4,1⁺] Template:CDD
Orbifold	(*442)			(*2222)	(2*22)	(*2222)
Diagram
Coxeter		[4,4⁺] Template:CDD	[4⁺,4] Template:CDD	[(4,4,2⁺)] Template:CDD	[1⁺,4,1⁺,4] Template:CDD	[4⁺,4⁺] Template:CDD
Orbifold		(4*2)		(2*22)		(22×)
Rotational subgroups
Index	2	4			8
Diagram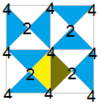
Coxeter	[4,4]⁺ Template:CDD	[1⁺,4,4⁺] Template:CDD	[4⁺,4,1⁺] Template:CDD	[(4,1⁺,4,2⁺)] Template:CDD	[1⁺,4,1⁺,4,1⁺] = [(4⁺,4⁺,2⁺)] Template:CDD
Orbifold	(442)			(2222)

The same set of 15 small subgroups exists on all triangle groups with even order elements, like [6,4] in the hyperbolic plane:

Small index subgroups of [6,4]
Subgroup index	1	2			4
Diagrams
Coxeter (orbifold)	[6,4] (*642) Template:CDD	[1⁺,6,4] Template:CDD (*443)	[6,4,1⁺] Template:CDD (*662)	[6,1⁺,4] Template:CDD (*3222)	[6,1⁺,4,1⁺] Template:CDD (2*33)	[1⁺,6,4,1⁺] Template:CDD (*3232)
Diagrams
Coxeter (orbifold)		[6,4⁺] Template:CDD (4*3)	[6⁺,4] Template:CDD (6*2)	[(6,4,2⁺)] Template:CDD (2*32)	[1⁺,6,1⁺,4] Template:CDD (3*22)	[6⁺,4⁺] Template:CDD (32×)
Rotational subgroups
Subgroup index	2	4			8
Diagrams
Coxeter (orbifold)	[6,4]⁺ (642) Template:CDD	[1⁺,6,4⁺] Template:CDD (443)	[6⁺,4,1⁺] Template:CDD (662)	[(6,1⁺,4,2⁺)] Template:CDD (3222)	[1⁺,6,1⁺,4,1⁺] = [(6⁺,4⁺,2⁺)] Template:CDD (3232)

Extended symmetry

47 year-old Podiatrist Hyslop from Alert Bay, has lots of hobbies and interests that include fencing, property developers in condo new launch singapore and handball. Just had a family trip to Monasteries of Haghpat and Sanahin.

Coxeter's notation includes double square bracket notation, [[X]] to express isomorphic symmetry within a Coxeter diagram. Johnson added alternative of angled-bracket <[X]> option as equivalent to square brackets for doubling to distinguish diagram symmetry through the nodes versus through the branches. Johnson also added a prefix symmetry modifier [Y[X]], where Y is the symmetry of the fundamental domain of [X].

For example in these equivalent rectangle and rhombic geometry diagrams of ${\tilde {A}}_{3}$ : Template:CDD and Template:CDD, the first doubled with square brackets, [[3^[4]]] or twice doubled as [2[3^[4]]], with [2], order 4 higher symmetry. To differentiate the second, angled brackets are used for doubling, <[3^[4]]> and twice doubled as <2[3^[4]]>, also with a different [2], order 4 symmetry. Finally a full symmetry where all 4 nodes are equivalent can be represented by [4[3^[4]]], with the order 8, [4] symmetry of the square.

Further symmetry exists in the cyclic ${\tilde {A}}_{n}$ and branching $D_{3}$ , ${\tilde {E}}_{6}$ , and ${\tilde {D}}_{4}$ diagrams. ${\tilde {A}}_{n}$ graph has order 2n symmetry of a regular n-gon, {n}, and is represented by [n[3^[n]]]. $D_{3}$ and ${\tilde {E}}_{6}$ are represented by [3[3^1,1,1]] = [3,4,3] and [3[3^2,2,2]] respectively while ${\tilde {D}}_{4}$ by [(3,3)[3^1,1,1,1]] = [3,3,4,3], with the diagram containing the order 24 symmetry of the regular tetrahedron, {3,3}. The noncompact hyperbolic group graph ${\bar {L}}_{5}$ = [3^1,1,1,1,1], Template:CDD, contains the symmetry of a 5-cell, {3,3,3}, and thus is represented by [(3,3,3)[3^1,1,1,1,1]] = [3,4,3,3,3].

A "*" superscript is effectively an inverse operation, creating radial subgroups removing connected of odd-ordered mirrors.^[2]

Examples:

Extended groups	Radial subgroups	Coxeter diagrams	Index
[3[2,2]] = [4,3]	[4,3^*] = [2,2]	Template:CDD = Template:CDD	6
[(3,3)[2,2,2]] = [4,3,3]	[4,(3,3)^*] = [2,2,2]	Template:CDD = Template:CDD	24
[1[3^1,1]] = [[3,3]] = [3,4]	[3,4,1⁺] = [3,3]	Template:CDD = Template:CDD	2
[3[3^1,1,1]] = [3,4,3]	[3^*,4,3] = [3^1,1,1]	Template:CDD = Template:CDD	6
[2[3^1,1,1,1]] = [4,3,3,4]	[1⁺,4,3,3,4,1⁺] = [3^1,1,1,1]	Template:CDD = Template:CDD	4
[3[3,3^1,1,1]] = [3,3,4,3]	[3^*,4,3,3] = [3^1,1,1,1]	Template:CDD = Template:CDD	6
[(3,3)[3^1,1,1,1]] = [3,4,3,3]	[3,4,(3,3)^*] = [3^1,1,1,1]	Template:CDD = Template:CDD	24
[2[3,3^1,1,1,1]] = [3,(3,4)^1,1]	[3,(3,4,1⁺)^1,1] = [3,3^1,1,1,1]	Template:CDD = Template:CDD	4
[(2,3)[^1,13^1,1,1]] = [4,3,3,4,3]	[1⁺,4,3,3,4,3⁺] = [3^1,1,1,1,1]	Template:CDD = Template:CDD	12
[(3,3)[3,3^1,1,1,1]] = [3,3,4,3,3]	[3,3,4,(3,3)^*] = [3^1,1,1,1,1]	Template:CDD = Template:CDD	24
[(3,3,3)[3^1,1,1,1,1]] = [3,4,3,3,3]	[3,4,(3,3,3)^*] = [3^1,1,1,1,1]	Template:CDD = Template:CDD	120

Extended groups	Radial subgroups	Coxeter diagrams	Index
[1[3^[3]]] = [3,6]	[3,6,1⁺] = [3^[3]]	Template:CDD = Template:CDD	2
[3[3^[3]]] = [6,3]	[6,3^*] = [3^[3]]	Template:CDD = Template:CDD	6
[1[3,3^[3]]] = [3,3,6]	[3,3,6,1⁺] = [3,3^[3]]	Template:CDD = Template:CDD	2
[(3,3)[3^[3,3]]] = [6,3,3]	[6,(3,3)^*] = [3^[3,3]]	Template:CDD = Template:CDD	24
[1[∞]²] = [4,4]	[4,1⁺,4] = [∞]² = [∞]×[∞] = [∞,2,∞]	Template:CDD = Template:CDD	2
[2[∞]²] = [4,4]	[1⁺,4,4,1⁺] = [(4,4,2^*)] = [∞]²	Template:CDD = Template:CDD	4
[4[∞]²] = [4,4]	[4,4^*] = [∞]²	Template:CDD = Template:CDD	8
[2[3^[4]]] = [4,3,4]	[1⁺,4,3,4,1⁺] = [(4,3,4,2^*)] = [3^[4]]	Template:CDD = Template:CDD	4
[3[∞]³] = [4,3,4]	[4,3^*,4] = [∞]³ = [∞,2,∞,2,∞]	Template:CDD = Template:CDD	6
[(3,3)[∞]³] = [4,3^1,1]	[4,(3^1,1)^*] = [∞]³	Template:CDD = Template:CDD	24
[(4,3)[∞]³] = [4,3,4]	[4,(3,4)^*] = [∞]³	Template:CDD = Template:CDD	48
[(3,3)[∞]⁴] = [4,3,3,4]	[4,(3,3)^*,4] = [∞]⁴	Template:CDD = Template:CDD	24
[(4,3,3)[∞]⁴] = [4,3,3,4]	[4,(3,3,4)^*] = [∞]⁴	Template:CDD = Template:CDD	384

Looking at generators, the double symmmetry is seen as adding a new operator that maps symmetric positions in the Coxeter diagram, making some original generators redundant. For 3D space groups, and 4D point groups, Coxeter defines an index two subgroup of [[X]], [[X]⁺], which he defines as the product of the original generators of [X] by the doubling generator. This looks similar to [[X]]⁺, which is the chiral subgroup of [[X]]. So for example the 3D space groups [[4,3,4]]⁺ (I432, 211) and [[4,3,4]⁺] (PmTemplate:Overlinen, 223) are distinct subgroups of [[4,3,4]] (ImTemplate:Overlinem, 229).

Computation with reflection matrices as symmetry generators

A Coxeter group, represented by Coxeter diagram Template:CDD, is given Coxeter notation [p,q] for the branch orders. Each node in the Coxeter diagram represents a mirror, by convention called ρ_i (and matrix R_i). The generators of this group [p,q] are reflections: ρ₁, ρ₂, and ρ₃. Rotational subsymmetry is given as products of reflections: By convention, σ_1,2 (and matrix S_1,2) = ρ₁ρ₂ represents a rotation of angle π/p, and σ_2,3 = ρ₂ρ₃ is a rotation of angle π/q, and σ_1,3 = ρ₁ρ₃ represents a rotation of angle π/2.

[p,q]⁺ is an index 2 subgroup represented by two rotation generators, each a products of two reflections: σ_1,2, σ_2,3, and representing rotations of π/p, and π/q angles respectively.

If q is even, [p⁺,q] is another subgroup of index 2, represented by rotation generator σ_1,2, and reflectional ρ₃.

If both p and q are even, [p⁺,q⁺] is a subgroup of index 4 with a single generator type, constructed as a product of all three reflection matrices: By convention as: ψ_1,2,3 (and matrix U_1,2,3) = σ_1,2ρ₃ = ρ₁σ_2,3 = ρ₁ρ₂ρ₃, which is an improper rotation or roto-reflection, representing a reflection and rotation.

In the case of affine Coxeter groups like Template:CDD, or Template:CDD, one mirror, usually the last, is translated off the origin. A translation generator τ_1,2 (and matrix T_1,2) is constructed as the product of two (or an even number of) reflections, including the affine reflection. A trans-reflection (reflection plus a translation) can be the product of an odd number of reflections φ_1,2,3 (and matrix V_1,2,3), like the index 4 subgroup Template:CDD: [4⁺,4⁺].

Another composite generator, by convention as ζ (and matrix Z), represents the inversion, mapping a point to its inverse. For [4,3] and [5,3], ζ = (ρ₁ρ₂ρ₃)^{h/2, where h is 6 and 10 respectively, the Coxeter number for each family.}

Example, in 2D, the Coxeter group [p] is represented by two reflection matrices R₁ and R₂, The cyclic symmetry [p]⁺ is represented by rotation generator of matrix S_1,2.

R₁	R₂	S_1,2=R₁xR₂
$\left[{\begin{smallmatrix}1&0\\0&-1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}\cos 2\pi /p&\sin 2\pi /p\\\sin 2\pi /p&-\cos 2\pi /p\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}\cos 2\pi /p&\sin 2\pi /p\\-\sin 2\pi /p&\cos 2\pi /p\\\end{smallmatrix}}\right]$

A simple example affine group is [4,4] (p4m), can be given by three reflection matrices, constructed as a reflection across the x axis (y=0), a diagonal (x=y), and the affine reflection across the line (x=1). [4,4]⁺ (p4) is generated by S_1,2 S_2,3, and S_1,3. [4⁺,4⁺] (pgg) is generated by 2-fold rotation S_1,3 and trans-reflection V_1,2,3. [4⁺,4] (p4g) is generated by S_1,2 and R₃. The group [(4,4,2⁺)] (cmm), is generated by 2-fold rotation S_1,3 and reflection R₂.

R₁	R₂	R₃	S_1,2	S_2,3	S_1,3	V_1,2,3
$\left[{\begin{smallmatrix}1&0&0\\0&-1&0\\0&0&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}0&1&0\\1&0&0\\0&0&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}-1&0&2\\0&1&0\\0&0&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}0&1&0\\-1&0&0\\0&0&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}0&1&0\\-1&0&2\\0&0&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}-1&0&2\\0&-1&0\\0&0&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}0&1&0\\1&0&-2\\0&0&1\\\end{smallmatrix}}\right]$

Coxeter groups are categorized by their rank, being the number of nodes in its Coxeter graph. The structure of the groups are also given with their abstract group types: In this article, the abstract dihedral groups are represented as Dih_n, and cyclic groups are represented by Z_n, with Dih₁=Z₂.

Rank one groups

In one dimension, the bilateral group [ ] represents a single mirror symmetry, abstract Dih₁ or Z₂, symmetry order 2. It is represented as a Coxeter graph with a single node, Template:CDD. The identity group is the direct subgroup [ ]⁺, Z₁, symmetry order 1. The + superscript simply implies that alternate mirror reflections are ignored, leaving the identity group in this simplest case.

Group	Coxeter	Coxeter diagram	Order	Description
C₁	[ ]⁺		1	Identity
D₁	[ ]	Template:CDD	2	Reflection group

Rank two groups

In two dimensions, the rectangular group [2], abstract Dih₂, also can be represented as a direct product [ ]×[ ] or Z₂×Z₂, being the product of two bilateral groups, represents two orthogonal mirrors, with Coxeter graph, Template:CDD, with order 4. The 2 in [2] comes from linearization of the orthogonal subgraphs in the Coxeter graph, as Template:CDD, with explicit branch order 2. The rhombic group, [2]⁺, half of the rectangular group, the point reflection symmetry, Z₂, order 2.

Coxeter notation allows a 1 place-holder for lower rank groups, so [1] is the same as [ ], and [1]⁺ is the same as [ ]⁺. This may be done to imply the group exists in 2-dimensions rather than 1 dimension.

The full p-gonal group [p], abstract dihedral group Dih_p, (nonabelian for p>2), of order 2p, is generated by two mirrors at angle π/p, represented by Coxeter graph Template:CDD. The p-gonal subgroup [p]⁺, cyclic group Zp, of order p, generated by a rotation angle of π/p.

Coxeter notation uses double-bracking to represent an automorphic doubling of symmetry by adding a bisecting mirror to the fundamental domain. For example [[p]] adds a bisecting mirror to [p], and is isomorphic to [2p].

In the limit, going down to one dimensions, the full apeirogonal group is obtained when the angle goes to zero, so [∞], abstractly the infinite dihedral group Dih_∞, represents two parallel mirrors and has a Coxeter graph Template:CDD. The apeirogonal group [∞]⁺, abstractly the infinite cyclic group Z_∞, isomorphic to the additive group of the integers, is generated by a single nonzero translation.

In the hyperbolic plane, there's a full pseudogonal group [πi/λ], and pseudogonal subgroup [πi/λ]⁺. These groups exist in regular infinite sided polygons, with edge length λ. The mirrors are all orthogonal to a single line.

Group	Intl	Orbifold	Coxeter	Order	Description
Finite
Z_n	n	n•	[n]⁺	n	Cyclic: n-fold rotations. Abstract group Z_n, the group of integers under addition modulo n.
D_n	nm	*n•	[n]	2n	Dihedral: cyclic with reflections. Abstract group Dih_n, the dihedral group.
Affine
Z_∞	∞	∞•	[∞]⁺	∞	Cyclic: apeirogonal group. Abstract group Z_∞, the group of integers under addition.
Dih_∞	∞m	*∞•	[∞]	∞	Dihedral: parallel reflections. Abstract infinite dihedral group Dih_∞.
Hyperbolic
Z_∞			[πi/λ]⁺	∞	pseudogonal group
Dih_∞			[πi/λ]	∞	full pseudogonal group

Rank three groups

47 year-old Podiatrist Hyslop from Alert Bay, has lots of hobbies and interests that include fencing, property developers in condo new launch singapore and handball. Just had a family trip to Monasteries of Haghpat and Sanahin.

In three dimensions, the full orthorhombic group [2,2], astracttly Z₂×Dih₂, order 8, represents three orthogonal mirrors, and also can be represented by Coxeter graph as three separate dots Template:CDD. It can also can be represented as a direct product [ ]×[ ]×[ ], but the [2,2] expression allows subgroups to be defined:

First there is a semidirect subgroup, the orthorhombic group, [2,2⁺], abstractly Dih₁×Z₂=Z₂×Z₂, of order 4. When the + superscript is given inside of the brackets, it means reflections generated only from the adjacent mirrors (as defined by the Coxeter graph, Template:CDD) are alternated. In general, the branch orders neighboring the + node must be even. In this case [2,2⁺] and [2⁺,2] represent two isomorphic subgroups that are geometrically distinct. The other subgroups are the pararhombic group [2,2]⁺, also order 4, and finally the central group [2⁺,2⁺] of order 2.

Next there is the full ortho-p-gonal group, [2,p], abstractly Dih₁×Dih_p=Z₂×Dih_p, of order 4p, representing two mirrors at a dihedral angle π/p, and both are orthogonal to a third mirror. It is also represented by Coxeter graph as Template:CDD.

The direct subgroup is called the para-p-gonal group, [2,p]⁺, abstractly Dih_p, of order 2p, and another subgroup is [2,p⁺] abstractly Z_p×Z₂, also of order 2p.

The full gyro-p-gonal group, [2⁺,2p], abstractly Dih_2p, of order 4p. The gyro-p-gonal group, [2⁺,2p⁺], abstractly Z_2p, of order 2p is a subgroup of both [2⁺,2p] and [2,2p⁺].

The polyhedral groups are based on the symmetry of platonic solids, the tetrahedron, octahedron, cube, icosahedron, and dodecahedron, with Schläfli symbols {3,3}, {3,4}, {4,3}, {3,5}, and {5,3} respectively. The Coxeter groups for these are called in Coxeter's bracket notation [3,3], [3,4], [3,5] called full tetrahedral symmetry, octahedral symmetry, and icosahedral symmetry, with orders of 24, 48, and 120. The front-to-back order can be reversed in the Coxeter notation, unlike the Schläfli symbol.

The tetrahedral group, [3,3], has a doubling [[3,3]] which maps the first and last mirrors onto each other, and this produces the [3,4] group.

In all these symmetries, alternate reflections can be removed producing the rotational tetrahedral, octahedral, and icosahedral groups of order 12, 24, and 60. The octahedral group also has a unique subgroup called the pyritohedral symmetry group, [3⁺,4], of order 12, with a mixture of rotational and reflectional symmetry.

In the Euclidean plane there's 3 fundamental reflective groups generated by 3 mirrors, represented by Coxeter graphs Template:CDD, Template:CDD, and Template:CDD, and are given Coxeter notation as [4,4], [6,3], and [(3,3,3)]. The parentheses of the last group imply the graphic cyclic, and also has a shorthand notation [3^[3]].

[[4,4]] as a doubling of the [4,4] group produced the same symmetry rotated π/4 from the original set of mirrors.

Direct subgroups of rotational symmetry are: [4,4]⁺, [6,3]⁺, and [(3,3,3)]⁺. [4⁺,4] and [6,3⁺] represent mixed reflectional and rotational symmetry.

Tetrahedral symmetry	Octahedral symmetry

Icosahedral symmetry

Finite

Intl^*	Geo ^[3]	Orbifold	Schönflies	Conway	Coxeter	Order
1	Template:Overline	1	C₁	C₁	[ ]⁺	1
Template:Overline	Template:Overline	×1	C_i = S₂	CC₂	[2⁺,2⁺]	2
Template:Overline = m	1	*1	C_s = C_1v = C_1h	±C₁ = CD₂	[ ]	2
2 3 4 5 6 n	Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline	22 33 44 55 66 nn	C₂ C₃ C₄ C₅ C₆ C_n	C₂ C₃ C₄ C₅ C₆ C_n	[2]⁺ [3]⁺ [4]⁺ [5]⁺ [6]⁺ [n]⁺	2 3 4 5 6 n
2mm 3m 4mm 5m 6mm nmm nm	2 3 4 5 6 n	22 33 44 55 66 nn	C_2v C_3v C_4v C_5v C_6v C_nv	CD₄ CD₆ CD₈ CD₁₀ CD₁₂ CD_2n	[2] [3] [4] [5] [6] [n]	4 6 8 10 12 2n
2/m 3/m 4/m 5/m 6/m n/m	Template:Overline 2 Template:Overline 2 Template:Overline 2 Template:Overline 2 Template:Overline 2 Template:Overline 2	2* 3* 4* 5* 6* n*	C_2h C_3h C_4h C_5h C_6h C_nh	±C₂ CC₆ ±C₄ CC₁₀ ±C₆ ±C_n / CC_2n	[2,2⁺] [2,3⁺] [2,4⁺] [2,5⁺] [2,6⁺] [2,n⁺]	4 6 8 10 12 2n
Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline	Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline	2× 3× 4× 5× 6× n×	S₄ S₆ S₈ S₁₀ S₁₂ S_2n	CC₄ ±C₃ CC₈ ±C₅ CC₁₂ CC_2n / ±C_n	[2⁺,4⁺] [2⁺,6⁺] [2⁺,8⁺] [2⁺,10⁺] [2⁺,12⁺] [2⁺,2n⁺]	4 6 8 10 12 2n

Intl	Geo	Orbifold	Schönflies	Conway	Coxeter	Order
222 32 422 52 622 n22 n2	Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline Template:Overline	222 223 224 225 226 22n	D₂ D₃ D₄ D₅ D₆ D_n	D₄ D₆ D₈ D₁₀ D₁₂ D_2n	[2,2]⁺ [2,3]⁺ [2,4]⁺ [2,5]⁺ [2,6]⁺ [2,n]⁺	4 6 8 10 12 2n
mmm Template:Overlinem2 4/mmm Template:Overlinem2 6/mmm n/mmm Template:Overlinem2	2 2 3 2 4 2 5 2 6 2 n 2	222 223 224 225 226 22n	D_2h D_3h D_4h D_5h D_6h D_nh	±D₄ DD₁₂ ±D₈ DD₂₀ ±D₁₂ ±D_2n / DD_4n	[2,2] [2,3] [2,4] [2,5] [2,6] [2,n]	8 12 16 20 24 4n
Template:Overline2m Template:Overlinem Template:Overline2m Template:Overlinem Template:Overline2m Template:Overline2m Template:Overlinem	4 Template:Overline 6 Template:Overline 8 Template:Overline 10 Template:Overline 12 Template:Overline n Template:Overline	22 23 24 25 26 2n	D_2d D_3d D_4d D_5d D_6d D_nd	±D₄ ±D₆ DD₁₆ ±D₁₀ DD₂₄ DD_4n / ±D_2n	[2⁺,4] [2⁺,6] [2⁺,8] [2⁺,10] [2⁺,12] [2⁺,2n]	8 12 16 20 24 4n
23	Template:Overline Template:Overline	332	T	T	[3,3]⁺	12
mTemplate:Overline	4 Template:Overline	3*2	T_h	±T	[3⁺,4]	24
Template:Overline3m	3 3	*332	T_d	TO	[3,3]	24
432	Template:Overline Template:Overline	432	O	O	[3,4]⁺	24
mTemplate:Overlinem	4 3	*432	O_h	±O	[3,4]	48
532	Template:Overline Template:Overline	532	I	I	[3,5]⁺	60
Template:Overline Template:Overlinem	5 3	*532	I_h	±I	[3,5]	120

Semiaffine

Intl	(orbifold)	Geo	Schönflies	Coxeter	Order
n	nn	Template:Overline	C_n	[1,n]⁺	n
nm	*nn	n	D_n	[1,n]	2n

IUC	(Orbifold)	Geo	Schönflies	Coxeter
p1	∞∞	pTemplate:Overline	C_∞	[1,∞]⁺
p1m1	*∞∞	p1	C_∞v	[1,∞]

IUC	(Orbifold)	Geo	Schönflies	Coxeter
p11g	∞x	p._g1	S_2∞	[∞⁺,2⁺]
p11m	∞*	p. 1	C_∞h	[∞⁺,2]
p2	22∞	pTemplate:Overline	D_∞	[∞,2]⁺
p2mg	2*∞	p2_g	D_∞d	[∞,2⁺]
p2mm	*22∞	p2	D_∞h	[∞,2]

Affine

IUC	(Orbifold)	Geometric	Coxeter
p2	(2222)	pTemplate:Overline	[1⁺,4,4]⁺
p2gg	(22x)	p_g2_g	[4⁺,4⁺]
p2mm	(*2222)	p2	[1⁺,4,4]
c2mm	(2*22)	c2	[[4⁺,4⁺]]
p4	(442)	pTemplate:Overline	[4,4]⁺
p4gm	(4*2)	p_g4	[4⁺,4]
p4mm	(*442)	p4	[4,4]

IUC	(Orbifold)	Geometric	Coxeter
p3	(333)	pTemplate:Overline	[1⁺,6,3⁺] = [3^[3]]⁺
p3m1	(*333)	p3	[1⁺,6,3] = [3^[3]]
p31m	(3*3)	h3	[6,3⁺] = [3[3^[3]]⁺]
p6	(632)	pTemplate:Overline	[6,3]⁺ = [3[3^[3]]]⁺
p6mm	(*632)	p6	[6,3] = [3[3^[3]]]

Subgroups

Given in Schönflies notation, Coxeter notation, (orbifold notation), some low index point subgroups are:

Reflection	Reflection subgroups	Rotation subgroup	Mixed	Improper rotation	Commutator subgroup
C_1v, [ ], (*)		C₁, [ ]⁺, (11)		S₂, [2⁺,2⁺], (×)	[ ]⁺
C_2v, [2], (*22)	[1⁺,2]=[ ] (*)	C₂, [2]⁺, (22)	C_2h, [2⁺,2], (2*)	S₄, [4⁺,2⁺], (2×)	[ ]⁺
C_nv, [n], (*nn)	[1⁺,2n]=[n] (*nn)	C_n, [n]⁺, (nn)	C_nh, [n⁺,2], (n*)	S_2n, [2n⁺,2⁺], (n×)	[n]⁺, n odd [n/2]⁺, n even
D_nh, [2,n], (*22n)	[1⁺,2,n]=[n] (*nn)	D_n, [2,n]⁺, (22n)	D_nd, [2⁺,2n], (2*n)		[n]⁺, n odd [n/2]⁺, n even
T_d, [3,3], (*332)		T, [3,3]⁺, (332)			[3,3]⁺, (332)
O_h, [4,3], (*432)	[1⁺,4,3]=[3,3] (*332)	O, [4,3]⁺, (432)	T_h, [3⁺,4], (3*2)		[3,3]⁺, (332)
I_h, [5,3], (*532)		I, [5,3]⁺, (532)			[5,3]⁺, (532)

Given in Coxeter notation, (orbifold notation), some low index affine subgroups are:

Reflective group	Reflective subgroup	Mixed subgroup	Rotation subgroup	Improper rotation/ translation	Commutator subgroup
[∞,2,∞], (*2222)	[1⁺,∞,2,∞], (*2222)	[∞⁺,2,∞], (**)	[∞,2,∞]⁺, (2222) [∞⁺,2⁺,∞⁺]⁺, (2222)	[∞⁺,2,∞⁺], (°) [∞⁺,2⁺,∞], (*×) [(∞,2)⁺,∞⁺], (××) [∞⁺,2⁺,∞⁺], (22×)	(2222)
[∞,2,∞], (*2222)	[1⁺,∞,2,∞], (*2222)	[∞,2⁺,∞], (222) [(∞,2)⁺,∞], (22)	[∞,2,∞]⁺, (2222) [∞⁺,2⁺,∞⁺]⁺, (2222)
[4,4], (*442)	[1⁺,4,4], (442) [4,1⁺,4], (2222) [1⁺,4,4,1⁺], (*2222)	[4⁺,4], (42) [(4,4,2⁺)], (222) [1⁺,4,1⁺,4], (2*22)	[4,4]⁺, (442) [1⁺,4,4⁺], (442) [1⁺,4,1⁺4,1⁺], (2222)	[4⁺,4⁺], (22×)
[3^[3]], (*333)		[3^[3]]⁺, (333)			(333)
[6,3], (*632)	[1⁺,6,3], (*333)	[3⁺,6], (3*3)	[6,3]⁺, (632) [1⁺,6,3⁺], (333)		(333)

Rank four groups

Finite isomorphism and correspondences	Subgroup relations

Point groups

DTZ's public sale group in Singapore auctions all forms of residential, workplace and retail properties, outlets, homes, lodges, boarding homes, industrial buildings and development websites. Auctions are at present held as soon as a month.

We will not only get you a property at a rock-backside price but also in an space that you've got longed for. You simply must chill out back after giving us the accountability. We will assure you 100% satisfaction. Since we now have been working in the Singapore actual property market for a very long time, we know the place you may get the best property at the right price. You will also be extremely benefited by choosing us, as we may even let you know about the precise time to invest in the Singapore actual property market.

The Hexacube is offering new ec launch singapore business property for sale Singapore investors want to contemplate. Residents of the realm will likely appreciate that they'll customize the business area that they wish to purchase as properly. This venture represents one of the crucial expansive buildings offered in Singapore up to now. Many investors will possible want to try how they will customise the property that they do determine to buy by means of here. This location has offered folks the prospect that they should understand extra about how this course of can work as well.

Singapore has been beckoning to traders ever since the value of properties in Singapore started sky rocketing just a few years again. Many businesses have their places of work in Singapore and prefer to own their own workplace area within the country once they decide to have a everlasting office. Rentals in Singapore in the corporate sector can make sense for some time until a business has discovered a agency footing. Finding Commercial Property Singapore takes a variety of time and effort but might be very rewarding in the long term.

is changing into a rising pattern among Singaporeans as the standard of living is increasing over time and more Singaporeans have abundance of capital to invest on properties. Investing in the personal properties in Singapore I would like to applaud you for arising with such a book which covers the secrets and techniques and tips of among the profitable Singapore property buyers. I believe many novice investors will profit quite a bit from studying and making use of some of the tips shared by the gurus." – Woo Chee Hoe Special bonus for consumers of Secrets of Singapore Property Gurus Actually, I can't consider one other resource on the market that teaches you all the points above about Singapore property at such a low value. Can you? Condominium For Sale (D09) – Yong An Park For Lease

In 12 months 2013, c ommercial retails, shoebox residences and mass market properties continued to be the celebrities of the property market. Models are snapped up in report time and at document breaking prices. Builders are having fun with overwhelming demand and patrons need more. We feel that these segments of the property market are booming is a repercussion of the property cooling measures no.6 and no. 7. With additional buyer's stamp responsibility imposed on residential properties, buyers change their focus to commercial and industrial properties. I imagine every property purchasers need their property funding to understand in value.

Rank four groups defined the 4-dimensional point groups: Template:3-sphere symmetry groups2

Subgroups

1D-4D reflective point groups and subgroups
Order	Reflection		Mixed subgroups	Improper rotation subgroups	Rotation subgroups	Commutator subgroup
2	[ ]	Template:CDD			[ ]⁺	[ ]⁺¹	[ ]⁺
4	[2]	Template:CDD			[2]⁺	[2]⁺²
8	[2,2]	Template:CDD	[2⁺,2]	[2⁺,2⁺]	[2,2]⁺	[2,2]⁺³
16	[2,2,2]	Template:CDD	[2⁺,2,2] [(2,2)⁺,2]	[2⁺,2⁺,2] [(2,2)⁺,2⁺] [2⁺,2⁺,2⁺]	[2,2,2]⁺ [2⁺,2,2⁺]	[2,2,2]⁺⁴
16	[2^1,1,1]	Template:CDD		[(2⁺)^1,1,1]		[2,2,2]⁺⁴
2n	[n]	Template:CDD			[n]⁺	[n]⁺¹	[n]⁺
4n	[2n]	Template:CDD			[2n]⁺	[2n]⁺²
4n	[2,n]	Template:CDD	[2,n⁺]		[2,n]⁺	[2,n]⁺²
8n	[2,2n]	Template:CDD	[2⁺,2n]	[2⁺,2n⁺]	[2,2n]⁺	[2,2n]⁺³
8n	[2,2,n]	Template:CDD	[2⁺,2,n] [2,2,n⁺]	[2⁺,(2,n)⁺]	[2,2,n]⁺ [2⁺,2,n⁺]	[2,2,n]⁺³
16n	[2,2,2n]	Template:CDD	[2,2⁺,2n]	[2⁺,2⁺,2n] [2,2⁺,2n⁺] [(2,2)⁺,2n⁺] [2⁺,2⁺,2n⁺]	[2,2,2n]⁺ [2⁺,2n,2⁺]	[2,2,2n]⁺⁴
	[2,2n,2]	Template:CDD		[2⁺,2n⁺,2⁺]
	[2n,2^1,1]	Template:CDD		[2n⁺,(2⁺)^1,1]
24	[3,3]	Template:CDD			[3,3]⁺	[3,3]⁺¹	[3,3]⁺
48	[3,3,2]	Template:CDD	[(3,3)⁺,2]		[3,3,2]⁺	[3,3,2]⁺²
48	[4,3]	Template:CDD	[4,3⁺]		[4,3]⁺	[4,3]⁺²
96	[4,3,2]	Template:CDD	[(4,3)⁺,2] [4,(3,2)⁺]		[4,3,2]⁺	[4,3,2]⁺³
96	[3,4,2]	Template:CDD	[3,4,2⁺] [3⁺,4,2]	[(3,4)⁺,2⁺]	[3⁺,4,2⁺]	[4,3,2]⁺³
120	[5,3]	Template:CDD			[5,3]⁺	[5,3]⁺¹	[5,3]⁺
240	[5,3,2]	Template:CDD	[(5,3)⁺,2]		[5,3,2]⁺	[5,3,2]⁺²	[5,3]⁺
4pq	[p,2,q]	Template:CDD	[p⁺,2,q]		[p,2,q]⁺ [p⁺,2,q⁺]	[p,2,q]⁺²	[p⁺,2,q⁺]
8pq	[2p,2,q]	Template:CDD	[2p,(2,q)⁺]	[2p⁺,(2,q)⁺]	[2p,2,q]⁺	[2p,2,q]⁺³
16pq	[2p,2,2q]	Template:CDD	[2p,2⁺,2q]	[2p⁺,2⁺,2q] [2p⁺,2⁺,2q⁺]	[2p,2,2q]⁺	[2p,2,2q]⁺⁴
120	[3,3,3]	Template:CDD			[3,3,3]⁺	[3,3,3]⁺¹	[3,3,3]⁺
192	[3^1,1,1]	Template:CDD			[3^1,1,1]⁺	[3^1,1,1]⁺¹	[3^1,1,1]⁺
384	[4,3,3]	Template:CDD	[4,(3,3)⁺]		[4,3,3]⁺	[4,3,3]⁺²	[3^1,1,1]⁺
1152	[3,4,3]	Template:CDD	[3⁺,4,3]		[3,4,3]⁺ [3⁺,4,3⁺]	[3,4,3]⁺²	[3⁺,4,3⁺]
14400	[5,3,3]	Template:CDD			[5,3,3]⁺	[5,3,3]⁺¹	[5,3,3]⁺

Space groups

Affine isomorphism and correspondences	35 cubic space groups in International, Fibrifold notation, and Coxeter notation

Template:List space groups Coxeter notation

Line groups

Rank four groups also defined the 3-dimensional line groups:

Semiaffine (3D)
Point group			Line group
Hermann-Mauguin		Schönflies	Hermann-Mauguin		Offset type	Wallpaper			Coxeter [∞_h,2,p_v]
Even n	Odd n	Schönflies	Even n	Odd n	Offset type	IUC	Orbifold	Diagram	Coxeter [∞_h,2,p_v]
n		C_n	Pn_q		Helical: q	p1	o		[∞⁺,2,n⁺]
Template:Overline	Template:Overline	S_2n	PTemplate:Overline	PTemplate:Overline	None	p11g, pg(h)	xx		[(∞,2)⁺,2n⁺]
n/m	Template:Overline	C_nh	Pn/m	PTemplate:Overline	None	p11m, pm(h)	**		[∞⁺,2,n]
2n/m		C_2nh	P2n_n/m		Zigzag	c11m, cm(h)	*x		[∞⁺,2⁺,2n]
nmm	nm	C_nv	Pnmm	Pnm	None	p1m1, pm(v)	**		[∞,2,n⁺]
nmm	nm	C_nv	Pncc	Pnc	Planar reflection	p1g1, pg(v)	xx		[∞⁺,(2,n)⁺]
2nmm		C_2nv	P2n_nmc		Zigzag	c1m1, cm(v)	*x		[∞,2⁺,2n⁺]
n22	n2	D_n	Pn_q22	Pn_q2	Helical: q	p2	2222		[∞,2,n]⁺
Template:Overline2m	Template:Overlinem	D_nd	PTemplate:Overline2m	PTemplate:Overlinem	None	p2mg, pmg(h)	22*		[(∞,2)⁺,2n]
Template:Overline2m	Template:Overlinem	D_nd	PTemplate:Overline2c	PTemplate:Overlinec	Planar reflection	p2gg, pgg	22x		[∞⁺,2⁺,2n⁺]
n/mmm	Template:Overline2m	D_nh	Pn/mmm	PTemplate:Overline2m	None	p2mm, pmm	*2222		[∞,2,n]
n/mmm	Template:Overline2m	D_nh	Pn/mcc	PTemplate:Overline2c	Planar reflection	p2mg, pmg(v)	22*		[∞,(2,n)⁺]
2n/mmm		D_2nh	P2n_n/mcm		Zigzag	c2mm, cmm	2*22		[∞,2⁺,2n]

Wallpaper groups

Rank four groups also defined some of the 2-dimensional wallpaper groups:

Affine (2D plane)

IUC	(Orbifold)	Geo	Coxeter
p1	(o)	pTemplate:Overline	[∞⁺,2,∞⁺]
p2	(2222)	pTemplate:Overline	[∞,2,∞]⁺
c2mm	(2*22)	c2	[∞,2⁺,∞]
p11g	(xx)	p_g1	h: [∞⁺,(2,∞)⁺]
p1g1	(xx)	p_g1	v: [(∞,2)⁺,∞⁺]
p2gm	(22*)	p_g2	h: [(∞,2)⁺,∞]
p2mg	(22*)	p_g2	v: [∞,(2,∞)⁺]

IUC	(Orbifold)	Geo	Coxeter
p11m	(**)	p1	h: [∞⁺,2,∞]
p1m1	(**)	p1	v: [∞,2,∞⁺]
p2mm	(*2222)	p2	[∞,2,∞]
c11m	(*x)	c1	h: [∞⁺,2⁺,∞]
c1m1	(*x)	c1	v: [∞,2⁺,∞⁺]
p2gg	(22x)	p_g2_g	[∞⁺,2⁺,∞⁺]
c2mm	(2*22)	c2	[∞,2⁺,∞]

Notes

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.

References

H.S.M. Coxeter:
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  - (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
  - (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
  
  My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- N.W. Johnson: Geometries and Transformations, Manuscript, (2011) Chapter 11: Finite symmetry groups
Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.

Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.

In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.

Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region

Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.

15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.

To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010
The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 Ch.22 35 prime space groups, ch.25 184 composite space groups, ch.26 Higher still, 4D point groups

↑ Coxeter and Moser, 1980, Sec 9.5 Commutator subgroup, p. 124-126
↑ Norman W. Johnson, Asia Ivić Weiss, Quaternionic modular groups, Linear Algebra and its Applications, Volume 295, Issues 1–3, 1 July 1999, Pages 159–189 [2]
↑ The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF [3]

[1] Coxeter and Moser, 1980, Sec 9.5 Commutator subgroup, p. 124-126

[2] Norman W. Johnson, Asia Ivić Weiss, Quaternionic modular groups, Linear Algebra and its Applications, Volume 295, Issues 1–3, 1 July 1999, Pages 159–189 [2]

[3] The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF [3]

[1]

[2]

[3]

Munn semigroup

Contents

Reflectional groups